EJERCICIO 4 DE SELECTIVIDAD Jun`13 B El tiempo que los

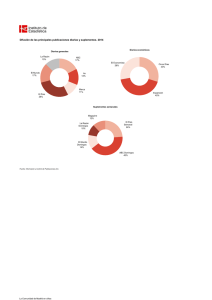
I.E.S. Los Pedroches. 2º de Bachillerato - Matemáticas II de las CC.SS. Curso 2013-14.
EJERCICIO 4 DE SELECTIVIDAD
Jun’13 B
El tiempo que los españoles dedican a ver la televisión los domingos es una variable aleatoria que sigue una
distribución Normal de media desconocida y desviación típica 75 minutos. Elegida una muestra aleatoria de
españoles se ha obtenido, para la media de esa distribución, el intervalo de confianza (188.18, 208.82), con un nivel
del 99%.
a) (1.5 puntos) Calcule la media muestral y el tamaño de la muestra.
b) (1.0 puntos) Calcule el error máximo permitido si se hubiese utilizado una muestra de tamaño 500 y un nivel
de confianza del 96%.
Sea X el tiempo dedicado a ver televisión los domingos para cada individuo de la población , y
sea X la media del tiempo dedicado a ver televisión los domingos para cada muestra de individuos.
a) IC ' (188,18 ; 208.82) ' ( x ± ε )
l %l
188,18 % 208,82
x ' der izq '
' 198,5 minutos .
2
2
l &l
208,82 & 188,18
ε ' der izq '
' 10,32 minutos .
2
2
Como la población de partida es normal: ε ' zα / 2 ·
ε
lizq
ε
x
σ
n
Datos: ε ' 10,32 ; zα/2 ' 2,58 (calculado abajo) ; σ ' 75 ; n ' ?
Nivel de confianza: 0,99 ' 1 & α Y α ' 1 & 0,99 ' 0,01
α
0,01
Por definición:
p (Z # zα / 2 ) ' 1 & ' 1 &
' 0,99500 Y zα / 2 ' 2,58 (por exceso).
2
2
75
2,58 · 75
2,58 · 75 2
Y n'
Por tanto: 10,32 ' 2,58 ·
Y n'(
) . 352 (por exceso siempre).
10,32
10,32
n
Conclusión:
la media muestral ha sido 198,5 minutos, y el tamaño de la muestra ha sido 352.
b) Como la población de partida es normal: ε ' zα / 2 ·
σ
n
Datos: ε ' ? ; zα/2 ' 2,06 (calculado abajo) ; σ ' 75 ; n ' 500 .
Nivel de confianza: 0,96 ' 1 & α Y α ' 1 & 0,96 ' 0,04
α
0,04
Por definición:
p (Z # zα / 2 ) ' 1 & ' 1 &
' 0,98000 Y zα / 2 ' 2,06 (por exceso).
2
2
75
' 6,91 minutos .
Por tanto: ε ' 2,06 ·
500
Conclusión:
el error máximo permitido hubiese sido 6,91 minutos.
lder