Soluciones a “Ejercicios y problemas”
Anuncio
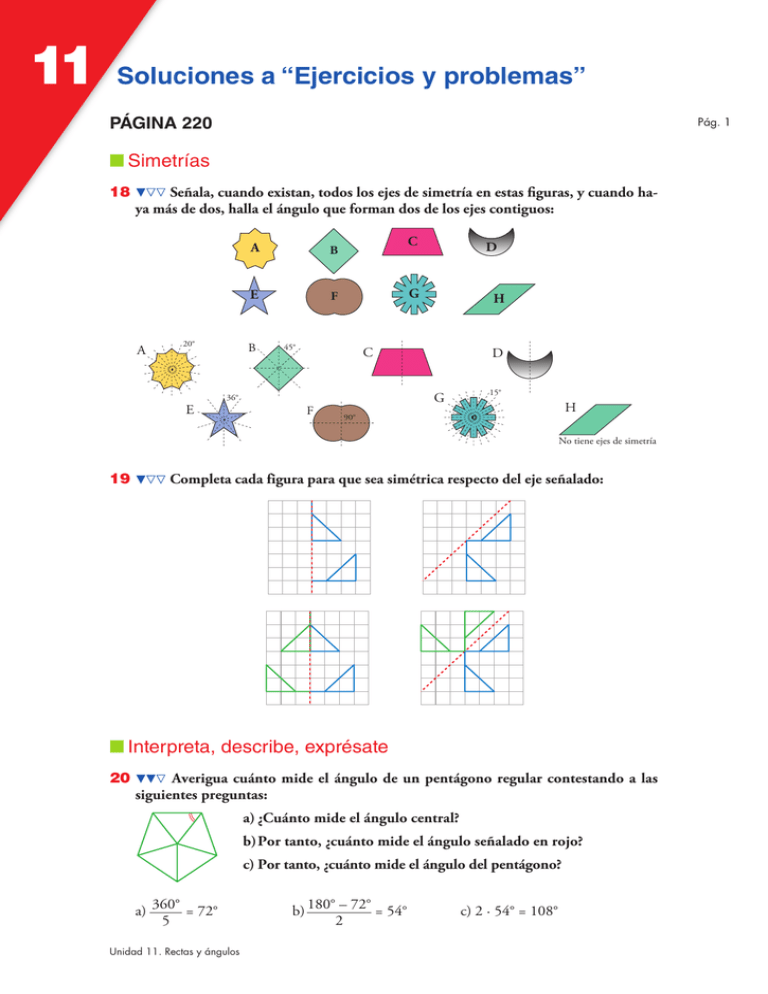
11 Soluciones a “Ejercicios y problemas” PÁGINA 220 Pág. 1 ■ Simetrías 18 Señala, cuando existan, todos los ejes de simetría en estas figuras, y cuando haya más de dos, halla el ángulo que forman dos de los ejes contiguos: A 20° E A B E F B 36° C D G 45° H C F D G 15° H 90° No tiene ejes de simetría 19 Completa cada figura para que sea simétrica respecto del eje señalado: ■ Interpreta, describe, exprésate 20 Averigua cuánto mide el ángulo de un pentágono regular contestando a las siguientes preguntas: a) ¿Cuánto mide el ángulo central? b) Por tanto, ¿cuánto mide el ángulo señalado en rojo? c) Por tanto, ¿cuánto mide el ángulo del pentágono? a) 360° = 72° 5 Unidad 11. Rectas y ángulos b) 180° – 72° = 54° 2 c) 2 · 54° = 108° 11 Soluciones a “Ejercicios y problemas” 21 ¿Es posible dibujar un triángulo rectángulo con un ángulo de 100°? Dibújalo o explica por qué no puede existir. No existe tal triángulo, ya que, como es rectángulo, uno de sus ángulos ha de medir 90°, y la suma de sus otros dos ángulos, 90° también. Por tanto, uno de esos ángulos no puede medir 100°. 22 Traza una circunferencia y un diámetro AB. Clava una chincheta en cada extremo del diámetro, coloca una goma elástica y, con un lápiz, forma un triángulo como muestra la ilustración: ì ì ì M M ì M M A B ì ¿Cómo evoluciona el ángulo M al desplazar la punta del lápiz sobre la circunferencia? Expón por escrito tus conclusiones y justifícalas. ì El ángulo M es de 90° en todas las posiciones en las que la punta del lápiz queda sobre la circunferencia, ya que es el ángulo inscrito correspondiente a un ángulo central de 180°. 23 Observa las letras del abecedario: Di cuáles no tienen ejes de simetría (hay 10), cuáles tienen un eje de simetría (hay 13), cuáles tienen dos (hay 3) y cuál tiene infinitos ejes de simetría. Dibuja cada una de ellas en tu cuaderno señalando los ejes que tenga. No tienen ejes de simetría: F, G, J, N, Ñ, P, Q, R, S, Z. Tienen un eje de simetría: A, B, C, D, E, K, L, M, T, U, V, W, Y. Así: A B C D E K M T U V W Y Tienen dos ejes de simetría: H, I, X. Así: H I X La O tiene infinitos ejes de simetría. Todas las rectas que pasen por el centro de la circunferencia son ejes de simetría. Unidad 11. Rectas y ángulos Pág. 2 11 Soluciones a “Ejercicios y problemas” 24 Completa la siguiente figura para que tenga los dos ejes de simetría que se indican: e1 e1 e2 25 e2 Vamos a obtener figuras mirando un trozo de esta figura F con un espejo: F Por ejemplo, para obtener la figura Z hemos de situar el espejo así: Z F Indica cómo hay que situar el espejo sobre F para visualizar cada una de las siguientes figuras: A B C D E P M N C B A D E N Unidad 11. Rectas y ángulos M P Pág. 3





