APLICACIONES DE LA INTEGRAL Volumen de un sólido de

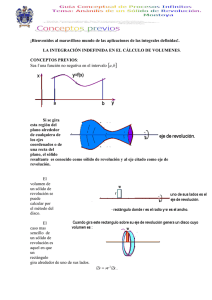
APLICACIONES DE LA INTEGRAL
Las aplicaciones del cálculo integral son muy variadas. En esta sección veremos algunas
de ellas:
♦ Volumen de un sólido de revolución (obtenido rotando en torno a los ejes
coordenados).
♦ Longitud de una curva
♦ Área de una superficie de revolución
Volumen de un sólido de revolución
Si bien la interpretación más natural para una integral definida es la del área encerrada
bajo la gráfica de una función positiva, no es ésta la única aplicación que en este sentido
tendremos. A través de razonamientos similares podemos calcular el volumen de un
sólido que se haya obtenido por medio de la rotación de una figura alrededor de un eje.
Para incorporar rápidamente estas aplicaciones tan sólo precisamos recordar que el
volumen de un cilindro es V = Ah , donde A es el área de la base y h es la altura.
Supongamos que el sólido es obtenido al rotar, en torno al eje x, la región del plano
limitada por el gráfico de f : f ( x) = x , el eje x y las rectas de ecuaciones x = 0 y
x=4.
Como se observa en la figura, ΔV = π ( x ) Δx , de donde obtenemos que el volumen de
2
4
este sólido es V = ∫ πxdx = 8π .
0
En general, en situaciones análogas a la planteada, podemos deducir que:
El volumen del sólido de revolución obtenido al girar en torno al eje x la región del
plano limitada por el gráfico de f, el eje x y las rectas de ecuaciones x = a y x = b es:
b
V =π
∫ ( f (x)) dx
2
a
Si la recta en torno a la cual rotamos la región de plano fuese el eje de las y, tendríamos,
como se observa en la figura,
ΔV = 2πxf ( x)Δx , por lo que:
El volumen del sólido de revolución obtenido al girar la región del plano limitada por el
gráfico de f, el eje x y las rectas de ecuaciones x = a y x = b es, en torno al eje y es:
b
∫
V = 2π xf ( x) dx
a
Ejemplo:
Queremos calcular el volumen del sólido que resulta cuando la región R de la figura
gira alrededor del eje y.
y = 3 + 2x - x2
3
(
)
Aplicando directamente el resultado anterior: V = 2π ∫ x 3 + 2 x − x 2 dx =
0
45
π
2
Longitud de una curva plana.
En esta instancia tan sólo veremos como encontrar la longitud de una curva plana
cuando ésta está dada a través del gráfico de una función y = f ( x) que sea derivable en
el intervalo correspondiente.
B
Δl
Δy
A
Δx
Calculemos la longitud de Δl teniendo en cuenta que la longitud de una curva de este
tipo es aproximadamente igual a la de la cuerda AB. Por lo tanto:
Δl =
(Δx )2 + (Δy )2
=
(Δx )2 ⎜⎜1 + (Δy )2 ⎟⎟ =
(Δx ) ⎠
⎝
⎛
2
⎞
⎛ ⎛ Δy ⎞ 2 ⎞
⎜1 + ⎜ ⎟ ⎟ Δx ,
⎜ ⎝ Δx ⎠ ⎟
⎝
⎠
Lagrange, llegamos a que:
2
Δl = 1 + ( f ' (~
x )) Δx
Razonando en forma análoga, obtenemos que:
que por el teorema de
La longitud del gráfico de f considerada el intervalo [a, b] es:
b
L=
∫
1 + ( f ' ( x ) ) dx
2
a
Ejemplo:
Queremos encontrar la longitud del arco de la curva de ecuación y = x 3 / 2 comprendido
entre los puntos (1,1) y (4,8).
Aplicando
4
L=
∫
1
directamente
el
4
resultado
9
8 ⎛ 3 / 2 13
⎛3
⎞
⎜10 −
1 + ⎜ x 1 / 2 ⎟ dx = 1 + x dx =
⎜
4
27
8
⎝2
⎠
⎝
1
3/ 2
∫
anterior:
⎞
⎟ (se sugiere verificar).
⎟
⎠
Área de una superficie de revolución
Supongamos que rotamos en torno al eje x el gráfico de una función positiva como la de
la figura. Cada parte de la curva de longitud Δl genera al girar en torno al eje x una
figura que podemos asemejar a un rectángulo.
∆l
2π f(x)
Las dimensiones de ese “rectángulo” son Δl de ancho y 2πf ( x) de largo. De ese modo
es que cada tira tiene un área Δá = 2πf ( x)Δl
x )) Δx
Como, a su vez, Δl = 1 + ( f ' (~
2
Tendríamos que Δá = 2πf ( x) 1 + ( f ' ( x )) Δx , por lo que
2
El área de la superficie de revolución obtenida al girar en torno al eje x la gráfica de f,
entre las rectas de ecuaciones x = a y x = b es:
b
A = 2π ∫ f ( x) 1+ ( f ' ( x)) dx
2
a
Ejemplo:
Busquemos el área de una esfera de radio a . Pensemos que la misma se obtiene como
superficie de revolución al girar una circunferencia de radio a en torno a uno de sus
diámetros.
Para ello consideremos la circunferencia de centro en el origen y radio a , cuya
2
2
2
ecuación más conocida es x + y = a . Si bien la circunferencia en cuestión no es el
gráfico de una función, puede descomponerse en el gráfico de dos funciones, las que
tienen como gráficos a las semi circunferencias de ecuaciones: y = a 2 − x 2
e
y = − a2 − x2 .
y = a2 − x2
y = − a2 − x2
Calcularemos el área de la superficie de revolución obtenida usando que la misma es
b
A = 2π ∫ f ( x) 1 + ( f ' ( x) ) dx en donde f : f ( x ) =
a
Por lo que
2
a2 − x2 .
a
A = 2π ∫ a − x
2
−a
2
⎛ −x
1 + ⎜⎜
2
2
⎝ a −x
2
a
⎞
⎟ dx =4π ∫ a 2 − x 2
⎟
0
⎠
1
a −x
2
Se sugiere que realice las operaciones y corrobore los cálculos.
Ejercicios
2
adx =4π a 2