Practica 3 - GFC
Anuncio

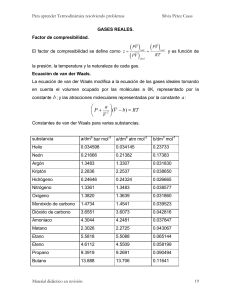
TERMODINAMICA Curso 2008 Practica 3: Potenciales Termodinámicos y Relaciones de Maxwell 1. Encontrar la ecuación fundamental de un gas ideal monoatómico en la representación de Helmholtz, en la entálpica y en la de Gibbs, considerando que la ecuación fundamental en la representación entrópica es: 3 −5 S (U , V , N ) = AN + NR ln⎛⎜U 2VN 2 ⎞⎟ . En todos los casos encuentre las ecuaciones de estado por ⎝ ⎠ diferenciación de la ecuación fundamental. 2. Para un sistema que obedece la siguiente ecuación fundamental: S = C ( NVU hallar la energía libre de Gibbs y calcular: α (T , P ) , κ T (T , P ) y c p (T , P ) . ) 3 , con C una constante, 1 3. Un mol de gas Neon se encuentra en un cilindro con un pistón móvil en uno de sus extremos, el cual se encuentra en contacto con la presión atmosférica. Considerando al gas como ideal determinar el calor que debe darse al sistema para expandirlo de 20 a 50 litros. 4. Considere un gas cuyo estado es caracterizado por la energía libre F(T, V, N). a) Mostrar que la presión del gas es P = −⎛⎜ ∂ F ⎞⎟ . ⎝ ∂V ⎠ T b) Deducir F para un gas de van der Waals sabiendo que sus ecuaciones de estado son: P= N2 RT a . − 2 ; U vW = U ideal − a v−b v V c) Si se realiza una compresión isotérmica del volumen V al volumen V'. Obtener una expresión para la variación de energía libre para el gas ideal y para el gas de van der Waals. Comparar con el trabajo realizado sobre el gas en el curso de una compresión isotérmica reversible. 5. Considere un sistema homogéneo, una sola fase, definido por dos de las siguientes variables termodinámicas: P, V, T, energía interna U, entalpía H, entropía S, energía libre F y entalpía libre G. a) Escriba las expresiones diferenciales de las funciones de estado U, H, F, G, en función de las variables T, P, S, y V, precisando las condiciones de su validez. b) Deduzca las cuatro ecuaciones de Maxwell que relacionan a las derivadas parciales de S respecto de V y P con otras derivadas. 6. La experiencia de Joule consiste en la expansión libre de un gas confinado en volumen Vi a una presión Pi y temperatura Ti, en un recipiente contiguo en el cual se ha hecho vacío. En este proceso la energía interna permanece constante. a) Probar que si el gas es ideal la temperatura no cambia durante la expansión. b) Probar que para un gas que obedece la ecuación de estado de van der Waals la variación de la temperatura esta dada por: ∆T = T - T = 2aN ⎛⎜ 1 − 1 ⎞⎟ f i 3R ⎜⎝ Vf Vi ⎟⎠ 6 2 3 c) Calcular ∆T máximo para O2 (a = 0,1378 Pa m /mol , b=0,03183 m /mol) y para CO2 (a = 0,3639 Pa 6 2 3 3 3 m /mol , b = 0,04267 m /mol), suponiendo Vi = 10- m y N = 1. 7. Se comprime reversiblemente de 1 a 10 atm una cierta masa m de hexano líquido a la temperatura T = 300 K en un recipiente de paredes adiabáticas. Determinar la magnitud y el signo de la variación de temperatura ∆T 3 del liquido (la cual será pequeña ∆T<<T). Sabiendo que para hexano la densidad ρ = 0,7 gr/cm , el -3 -1 coeficiente de dilatación isobárico α = 1,3 10 K , y la capacidad calorífica por unidad de masa (calor especifico) a presión constante cp = 25 J/gr K. 8. En el experimento de Joule-Thompson un gas a alta presión se deja pasar a través de un tabique poroso a una región de baja presión. Al final de este proceso irreversible la entalpía permanece constante. Dependiendo de ciertas condiciones el gas se enfría o calienta al pasar por el tabique. a) Para un mol de gas que obedece la ecuación de estado de van der Vaals, obtenga una expresión para el coeficiente de Joule-Thompson a bajas presiones. ¿Qué ocurre con un gas ideal?. b) Muestre que para enfriar un gas que obedece la ecuación de van der Waals, es necesario que T<Ti, 2a siendo la temperatura de inversión Ti = . Rb c) Obtenga el valor del coeficiente de Joule-Thompson para N2 si cp = 29,2 J/mol K y T=273K. Calcule la variación de temperatura si la diferencia de presión es de 2 atm y la temperatura inicial T = 273 K. (R = 6 2 6 3 8,32 J/mol K, a = 0,139 Pa m /mol y b = 39,1 10- m /mol). TERMODINAMICA Curso 2008 9. Probar que si CV y CP son ⎛ ∂ ln T a) ⎛⎜ ∂ U ⎞⎟ = CV ⎜ ⎝ ∂ T ⎠ S ,N ⎝ ∂ ln P las capacidades caloríficas a volumen y presión constate, respectivamente: ⎞ ⎛ ∂H ⎞ ⎛ ∂ ln T ⎞ , y b) ⎜ = CP ⎜ ⎟ ⎟ ⎟ ⎠ V ,N ⎝ ∂T ⎠ S , N ⎝ ∂ ln V ⎠ P , N 10. Probar la siguiente relación c p = cV + Tvα 2 (1) y en particular probar para un gas ideal monoatómico: KT cV = 3 / 2 R; α = T −1 ; K T = P −1 ; c P = 5 / 2 R , verificando con estos valores la relación (1).