Hasta en las mejores familias…

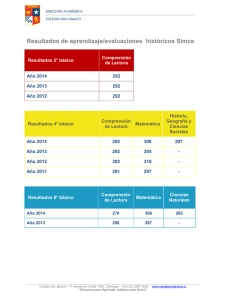
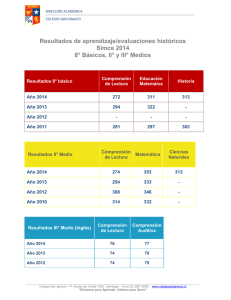
Hasta en las mejores familias…
El caso del Banco Mundial
Ignacio Vélez Pareja
Profesor
Universidad Tecnológica de Bolívar
http://www.cashflow88.com/decisiones/decisiones.html
[email protected]
[email protected]
Autoridad mundial

El Banco Mundial ha jugado un papel muy
importante en el desarrollo del Tercer mundo.
Reconocemos este liderazgo y la influencia que
tiene en oficinas de planeación, bancos centrales,
expertos y consultores. Por esta misma razón es
crítico examinar los procedimientos que se
utilizan para evaluar proyectos de inversión. Esta
práctica de instituciones internacionales influyen
también en la práctica de valoración y evaluación
de proyectos en el ámbito privado.
03/02/2012
Ignacio Vélez Pareja
2
Por eso es importante
Examinar lo que promueven estas entidades (Banco
Mundial, Banco Interamericano de Desarrollo
(BID), ONUDI, FONADE, Banco de la
República, etc.
03/02/2012
Ignacio Vélez Pareja
3
Áreas de mejora en los modelos

1.
2.
3.


Se muestran áreas donde se pueden hacer mejoras para la
valoración y fijación de tarifas. Algunas de ellas son:
Valoración a precios corrientes
Uso de CPC variable
Consistencia en flujos de caja y valores
El análisis se basó en un modelo para valoración de
infraestructura eléctrica que se encuentra en Financial
Modeling of Regulatory Policy del International Bank for
Reconstruction and Development – The World Bank 2002.
En esa referencia se encuentra el trabajo de Estache, A., Rodriguez Pardina Martín,
Rodríguez, Jose María, and Germán Sember, An Introduction to Financial and
Economic Modeling for Utility Regulators, The World Bank, 2002.que describe el
modelo.
03/02/2012
Ignacio Vélez Pareja
4
… no se puede resolver…





“En una empresa regulada el objetivo de la regulación es determinar los
ingresos requeridos y estos dependen de los costos (incluido el costo de
capital) esa es la fuente de circularidad que sigo creyendo no se puede
resolver. De hecho el problema más que de circularidad es de
indeterminación. Tenés una sola ecuación
Ki-S(ING-O&M-T-INV)/(1+r)=0
Ki es capital al inicio del periodo, ING ingresos requeridos (a su vez
son T*Q) Tarifas * cantidades, O&M costos de operación y
mantenimiento, T impuestos, INV inversiones
donde el objetivo es determinar las tarifas que permitan el equilibrio de
la firma. Con esa sola ecuación no se puede determinar Ki (valor del
capital inicial) e ING simultáneamente.”
Correspondencia privada con M. Rodríguez Pardina.
03/02/2012
Ignacio Vélez Pareja
5
No es posible su utilización.


“Respecto de los valores de mercado (para los
ponderadores) si bien eso es lo teóricamente correcto
aparecen dos problemas. Primero, en la mayoría de
nuestros países no hay valor de mercado para la
deuda de las empresas. Segundo el valor de mercado
del equity tiene un problema de circularidad (depende
directamente de las tarifas que queremos estimar con
el costo de capital) y por lo tanto no es posible su
utilización.”
Correspondencia privada con M. Rodríguez Pardina.
03/02/2012
Ignacio Vélez Pareja
6
… el BM NO tiene un modelo…


“[…] me sorprende muchísimo el titulo del email:
"modelo WB..."....es algo que no existe!; el Banco
NO tiene un modelo especifico para cualquier
país o cualquier sector […] Lo único que no
cambia es el criterio de decision: TIR=CoC. […]
(un detalle: en muchos países....no tenemos
valores de mercado...simplemente porque no hay
mercado).”
Correspondencia privada con A. Estache.
03/02/2012
Ignacio Vélez Pareja
7
Ignorar los impuestos


“Tratándose de empresas reguladas si las reglas impositivas son iguales
a las del resto de la economía hay argumentos para ignorar los
efectos impositivos (igual que las depreciaciones aceleradas por
ejemplo) ya que son comunes a toda la economía y por lo tanto la
empresa podrá beneficiarse o sufrirlos en la misma medida que los
mercados competitivos. Si uno incluye todo el detalle de efectos
quita a la empresa todo incentivo a optimizar su apalancamiento
por un lado y su política impositiva por el otro. Si la revisión es
prospectiva, como debería ser en un price cap, el costo de capital es
el esperado para las condiciones que se están modelando y
cualquier apartamiento futuro entre valores estimados y valores
realizados (que de lugar a la realización o no del tax shield entre
otros muchos elementos) sería parte del riesgo del negocio (por ello
el riesgo del price cap es mayor que la regulación por RoR ). “
Correspondencia privada con A. Estache.
03/02/2012
Ignacio Vélez Pareja
8
El diálogo es con Vivien


“Cualquier debate metodológico especifico a un país
está manejado de manera muy especifica en el Banco:
el diálogo país lo manejan directamente los
economistas que manejan el diálogo con los gobiernos
específicamente a sus cargos. Para Colombia, la
persona es Vivien Foster que copio en este mail. “
Correspondencia privada con A. Estache.
03/02/2012
Ignacio Vélez Pareja
9
Yo no fui…


“La verdad es que yo no he participado en el
desarrollo de este modelo. Por lo tanto, estoy
dirigiendo su mensaje a Martín Rodríguez Pardina
quien estuvo a cargo de su desarrollo, y podrá
responder a las críticas que usted avanza.”
Correspondencia privada con Vivien Foster.
03/02/2012
Ignacio Vélez Pareja
10
¿Cuál es el problema?


[M]i planteamiento va más allá del ejemplo pedagógico […]. El
problema que planteo señala (o cuestiona) la metodología en
general que se usa (o que se promueve) en el Banco Mundial para
evaluación (valoración) de proyectos. Estas metodologías […] son
las que el Banco utiliza en sus entrenamientos […].
[…] lo que está en juego no es un caso aislado de un modelo
pedagógico […]. Lo que está en juego es que con esas metodologías
es posible y probable que el Banco le de luz verde a proyectos que
no son deseables. Lo que está en juego son los recursos (siempre
limitados) que asigna el Banco a proyectos que tienen gran impacto
social en los países en desarrollo.
[…]
¿Hay alguna persona dentro del Banco con quien se pudiera
conversar al respecto de mis inquietudes?
Correspondencia privada con Vivien Foster.
03/02/2012
Ignacio Vélez Pareja
11
Esperemos…


Desde el 27 de julio está en manos de Ede IjjaszVásquez, Manager del Water and Sanitation
Program del Banco Mundial.
El día 2 de agosto de 2004 se recibió un conjunto
de comentarios de Martín Rodríguez Pardina. Ese
mismo día se dio respuesta. La correspondencia
se encuentra como apéndice en el documento base
de esta presentación
03/02/2012
Ignacio Vélez Pareja
12
Descripción del Modelo


Este modelo calcula el valor de un proyecto de
infraestructura y fija los valores de las tarifas que
garanticen un VPN = 0.
En el modelo se usa la metodología de precios
constantes y descuentan los flujos con una tasa
deflactada (CPC). Construyen el estado de
resultados y el balance general y de allí calculan
el FCL.
03/02/2012
Ignacio Vélez Pareja
13
La inflación ¿crea o destruye valor?




Si crea valor deberíamos estimularla.
Si es inocua no nos debe preocupar.
Si destruye, hay que combatirla.
Cuando se valora a precios constantes el valor no
se afecta por la inflación porque está fuera del
análisis. Cuando se usan corrientes se tiene en
cuenta en los flujos y en las tasas de descuento.
03/02/2012
Ignacio Vélez Pareja
14
¿Habrá diferencia en los valores?

Si como, dicen sólo es necesario ser consistentes (flujos
nominales, tasas nominales y flujos reales y tasas reales),
entonces la inflación no afectaría el valor. Sin embargo, la
inflación destruye el valor: a mayor inflación menor
valor. Entonces cuando se valora a constantes se produce
una sobrevaloración porque el valor en corrientes (que
tiene en cuenta la inflación) decrece a medida que la
inflación aumenta y en constantes permanece igual. Esto
significa que cuando hay inflación la diferencia entre
valor a constantes y a corriente es diferente de cero y
aumentará al aumentar la inflación.
03/02/2012
Ignacio Vélez Pareja
15
Ahorros en impuestos (AI)
Es el subsidio que se recibe del estado por hacer un
gasto. En este caso, se refiere a los gastos
financieros. Un gasto después de impuestos es igual
al gasto antes de impuestos por (1-T) y el ahorro en
impuesto es GT. En el caso de valoración es TKdD.
Se gana si hay suficiente UAII y si se pagan los
impuestos cuando se causan los intereses.
03/02/2012
Ignacio Vélez Pareja
16
Un ejemplo...
Estado de PyG simplificado
Ventas
1,000
1,000
500
500
0
200
Utilidad Neta A.I.
500
300
Impuestos (30%)
150
90
Utilidad Neta D.I
350
210
Costo de Ventas
Otros gastos
03/02/2012
Ignacio Vélez Pareja
17
¿Qué pasa si se aumentan los gastos?

Si los Otros gastos aumentaran en $200, la
primera reacción podría ser que la utilidad neta se
reducirá en $200, pero sólo se reduce en $140

G(1-T) = 200(1-30%) = 140
03/02/2012
Ignacio Vélez Pareja
18
Hay ahorros en impuestos

Un gasto incurrido en una firma que paga
impuestos, recibe un beneficio tributario o fiscal
igual a GT, donde T es la tasa de impuestos. Si se
incrementaron los gastos en $200 y se paga el
30% de impuestos, los gastos se convierten en
$140 por el ahorro de 30%×200 y $200 – $60 =
$140
03/02/2012
Ignacio Vélez Pareja
19
Ahorros en impuestos UAII>Int
En el caso de valoración es TKdD. Se gana si hay suficiente UAII y
si se pagan los impuestos cuando se causan los intereses. Observe
que el AI es T × Int = 40% × 150 = 60
Con deuda
Sin deuda
UAII
200
200
Intereses
150
0
Utilidad antes de impuestos
50
200
Impuestos 40%
20
80
Utilidad neta
30
120
AI = diferencia en impuestos
60
0
03/02/2012
Ignacio Vélez Pareja
20
Ahorros en impuestos UAII<Int
Con deuda
Sin deuda
UAII
100
100
Intereses
150
0
Utilidad antes de impuestos
-50
100
0
40
-50
60
40
0
Impuestos 40%
Utilidad neta
AI = diferencia en impuestos
Observe que ahora los ahorros en impuestos NO SON
T × Int = 40% × 150 = 60 sino 40. Esto ocurre porque no
hay suficiente UAII para ganarse los ahorros en
impuestos. En este caso el AI ganado en el año es
T × UAII = 40% × 100.
03/02/2012
Ignacio Vélez Pareja
21
El AI depende de UAII
1.
2.
3.

Si UAII > Intereses
entonces AI = T × Int
Si 0 < UAII < Intereses
entonces AI = T × UAII
Si UAII < 0 entonces AI
=0
Si hay amortización de
pérdidas, el AI perdido
en un año se puede
recuperar cuando haya
UAII.
03/02/2012

El CPC tradicional, CPC =
Kd × D% × (1 − T) + Ke × P%
aplica para el caso 1 si se
pagan los impuestos en el
mismo período. Es un caso
particular de
AIt
CPCt  Ku t ValTot t -1
Ignacio Vélez Pareja
22
¿Cómo se explica el (1-T) en el CPC?
Año Prést
0
1
Kd
AI
Año Prést
Neto
Neto
1.000
0
1.000
1.000
-1.300 120 -1.180
1
-1.300
-1.300
1.000
30%
18%
2
Kd

AI
120
30%
120
20%
Si la tasa de impuestos T es 40%, entonces el AI es 120. A la
izquierda tenemos impuestos pagados el mismo año y el AI ganado
en su totalidad el mismo año. Allí Kd después de impuestos es
Kd(1-T) = 30% × 60% = 18%. Al lado derecho Kd después de
impuestos NO ES Kd(1-T).
03/02/2012
Ignacio Vélez Pareja
23
El valor presente del AI por depreciación

La depreciación es un
gasto deducible, por lo
tanto genera un AI de T ×
D. Pero este valor no se
afecta por la metodología
(constantes o corrientes)
que se use. El VP es muy
diferente en constantes o
en corrientes. Esa
diferencia es la
sobrevaloración de los FC
03/02/2012
N
VP(AIdep ) K  
j1
TD
1  i real j
TD

j
j1 1  i nominal 
N
VP(AIdep ) ctes
VP(AIdep ) K  VP(AIdep ) ctes
VP(AIdep ) K - VP(AIdep ) ctes  0
Ignacio Vélez Pareja
24
Valoración a precios constantes




Cuando se usan precios constantes se incurre en sobrevaloración de los
flujos debido a los gastos de depreciación y a las cuentas por pagar. En este
caso el efecto de la depreciación es de 6,61% y el de las cuentas por pagar
es de 6,37%.
Se calculó el ahorro en impuestos por depreciación y se descontó a la tasa
real y a la nominal. La diferencia es la sobrevaluación.
Para las C×C se calculó su valor presente a la tasa real y se ajustaron los
valores por inflación descontados a la tasa nominal. La diferencia es la
sobrevaloración.
Lo adecuado es trabajar a precios corrientes haciendo proyecciones de la
inflación y los precios. La metodología de precios constantes sobreestima
el valor.
03/02/2012
Ignacio Vélez Pareja
25
Uso de D% constante en CPC cuando no lo es
D% usando los valores de mercado en el modelo presenta un valor
máximo de 0,71 y un mínimo de 0,20. Si se examina el D% en
libros el máximo es de 0,61 y el mínimo es de 0,04.
Activos
0
1
2
3
48,1 57,6 64,6 65,5
97,5 102,5 107,4 106,9
D% VL
0,49
Deuda
“VM” (BM)
92,82
D% “VM“ (BM)
03/02/2012
0,52
Ignacio Vélez Pareja
0,56
0,60
0,61
98,5 101,0
98,6
0,58
0,66
0,64
26
Inconsistencia en los flujos de caja



Desde finales de los años 50 y principios de los
60’s Modigliani y Miller M&M, en trabajos
iluminantes y seminales definieron la relación
entre los flujos de caja. Estos son el flujo de caja
libre FCL, el de la deuda, FCD, el del patrimonio,
FCA y el de los ahorros en impuestos, AI. La
relación es
FCL + AI = FCD + FCA
Esta relación no se cumple en el caso que se
analiza.
03/02/2012
Ignacio Vélez Pareja
27
Por ejemplo
Año
12
FCL
14,8 17,3 18,1
FCD
8,5
FCA
11,8 13,2 14,8
AI con Kd nominal 1,1
03/02/2012
13
9,9
1,0
14
9,4
0,8
FCL + TS
15,9 18,3 18,8
FCD + FCA
20,3 23,2 24,3
Diferencia
-3,5 -4,3 -4,9
Ignacio Vélez Pareja
28
Inconsistencia en los valores

En los mismos trabajos M&M establecieron una
relación similar para los valores de mercado.
Estos son el de la firma, calculado a partir del
FCL, el de los ahorros en impuestos, calculado a
partir de AI, el de la deuda, a partir del FCD y el
del patrimonio calculado a partir del FCA. La
relación es
VSD + VAI = VD + VP
03/02/2012
Ignacio Vélez Pareja
29
Por ejemplo
Valor Total = VP(FCL)
92,8
Patrimonio = VP(FCA)
36,2
Deuda = VP(FCL) – VP(FCA)
Deuda = VP(FCD)
Deuda del BG
Patrimonio = VP(FCL) - deuda del BG
56,6
48,1
48,1
44,7
Patrimonio = VP(FCL) – VP(FCD)
44,7
03/02/2012
Ignacio Vélez Pareja
30
Cálculo del costo de capital




Cuando la UAII es negativa o menor que los intereses los AI no se
ganan en el período que se analiza. Si hay amortización de pérdidas se
puede recuperar en años futuros. Esto significa que el CPC tradicional,
CPC = Kd × D% × (1 − T) + Ke × P% no se debe utilizar.
Los supuestos que hay detrás de este caso muy particular en el cual se
puede usar el CPC tradicional no se cumplen en el ejemplo del BM.
Para estas situaciones (y en general) se debe utilizar una formulación
más general:
AIt
CPCt  Ku t ValTot t -1
Donde AIt es el valor de los ahorros en impuestos del período t y
TotValt−1 es el valor de mercado de la firma para el período anterior.
Esto genera circularidad (que puede resolverse). Esto aplica si la tasa
de descuento de los AI es Ku
03/02/2012
Ignacio Vélez Pareja
31
Por ejemplo

El valor calculado a precios constantes por el BM es 98,2
y el calculado a precios constantes usando el CPC
adecuado es 84,5.
0
FCL
AI
CPC ajust = Ku-AI/TV
PV(FCL a CPCajust)
03/02/2012
84,5
Ignacio Vélez Pareja
1
-6,1
0,0
8,61%
97,8
2
-3,2
0,8
7,76%
108,5
3
3,0
1,3
7,45%
113,7
32
Sobreestimación del valor “correcto”

Al usar el FCC (FCC = FCL + AI) con un Ku real
se encuentra una diferencia de valor del 9,87%.
Esta diferencia es sólo la que ocurre por una
equivocada aplicación del CPC. No incluye la
sobrevaloración de C×C y depreciación ya
mencionadas.
03/02/2012
Ignacio Vélez Pareja
33
Forma de “cuadrar” los balances
Es común usar “plugs” para cuadrar los estados
financieros (el BG) Algunas veces pueden ser
correctos, pero otras pueden ocultar errores que
no se descubrirán jamás. Casi siempre se calculan
como la diferencia entre activos y pasivos y
patrimonio. Dependiendo del signo de esa
diferencia va a activos o a pasivos.
03/02/2012
Ignacio Vélez Pareja
34
Se usa este procedimiento



El FCA no es consistente con los datos de
balance. Se calcula una partida llamada
Debt/Petty cash como
Pasivos totales + patrimonio menos activos no
corrientes menos créditos por ventas netas menos
otros activos corrientes
Es más seguro usar el flujo de tesorería y hacer
los enlaces que dan consistencia a los tres estados
financieros.
03/02/2012
Ignacio Vélez Pareja
35
Mezcla de nominales y constantes



El ejemplo del BM usa precios constantes, pero
en los estados financieros incluyen los intereses ¡a
tasas corrientes”.
No se creía que esto ocurriera.
(Ver Vélez-Pareja, Ignacio, "Project Evaluation in an Inflationary Environment"
(February 11, 1999). Project Evaluation in an Inflationary Environment Working
Paper No. 2. http://ssrn.com/abstract=148410 y Vélez-Pareja, Ignacio and Tham,
Joseph, "Valuation in an Inflationary Environment" (May 31, 2002).
http://ssrn.com/abstract=329020)
03/02/2012
Ignacio Vélez Pareja
36
Una solución “apropiada”

Se reconstruyó el ejemplo para encontrar los AI
que toman en cuenta dos hechos: uno es que los
AI no se obtienen en el mismo período en que se
causan y segundo que los pagos de intereses se
deben calcular con un Kd real y no nominal.
Finalmente se calculó el FCA como
FCA = FCL + AI − FCD
03/02/2012
Ignacio Vélez Pareja
37
Cálculo “correcto”
Ku real
VP(FCC)
Deuda (BG)
Patrimonio = VP(FCC) − deuda (BS)
VP(FCA)

8,61%
84,5
48,1
36,4
36,4
Aquí se observa plena consistencia entre los valores.
03/02/2012
Ignacio Vélez Pareja
38
Recálculo de las tarifas

Con este valor se recalcularon las tarifas y se
encuentra que hay una subestimación de 6,8% y
8,2% para las dos categorías establecidas en el
modelo.
03/02/2012
Ignacio Vélez Pareja
39
Cálculo del Valor usando precios corrientes


Se ajustaron los ingresos, los costos y los gastos de
capital (inversiones) con la inflación que el modelo utiliza
para deflactar el CPC nominal. Esto implica inflación
neutral que es el supuesto implícito de precios constantes.
Con estas nuevas cifras y usando CPC basado en valores
de mercado se encuentra una sobrevaloración de 21,2%.
Esto implica una subestimación de las tarifas de 15,2% y
18,0%.
Por el otro lado, el D% a precios de mercado varía entre
0,22 y 0,63.
03/02/2012
Ignacio Vélez Pareja
40
A manera de resumen
Hemos indicado que se pueden hacer mejoras metodológicas
en las siguientes áreas:

En cuanto a la metodología de valoración (precios
corrientes en lugar de precios constantes)

Uso de endeudamiento variable (y CPC variable) en lugar
de constante.

Redefinición de flujos de caja tales como el FCA y el
FCD.

Consistencia entre los flujos

Consistencia entre los valores calculados

Adecuada valoración que evita la sobreestimación y

Cálculo apropiado de las tarifas para evitar subestimación.
03/02/2012
Ignacio Vélez Pareja
41
Con precios constantes

Esta tabla se ha calculado corrigiendo el hecho de los
intereses a precios corrientes, se corrigió el cálculo del
CPC para tener en cuenta el D% variable y se mantuvo la
metodología de precios constantes
Fuente
Cantidad
Sobreestimación en valor por D% y CPC constantes
9.87%
Sobreestimación en valor por depreciación
6.61%
Sobreestimación en valor por C×C
6.37%
Subestimación en tarifas (Primer bloque)
6.8%
Subestimación en tarifas (Segundo bloque)
8.2%
03/02/2012
Ignacio Vélez Pareja
42
Con precios corrientes

Para esta tabla se calculó el valor a precios corrientes y
teniendo en cuenta el D% variable. Se comparó con el
resultado obtenido por el Banco Mundial.
Sobreestimación total en valor comparando precios
constantes y corrientes
21,2%
Subestimación de tarifas (Primer bloque) con precios
corrientes
15,2%
Subestimación de tarifas (Segundo bloque) con precios
corrientes
18,0%
03/02/2012
Ignacio Vélez Pareja
43
Algunas conclusiones




Hemos sugerido algunas mejoras que se pueden hacer en el cálculo del
valor en un proyecto de infraestructura. La forma de evaluar propuesta
por entidades como el Banco Mundial, ONUDI, el BID etc. tienen
fuertes limitaciones.
Lo crítico de esto es la autoridad intelectual que representan entre
expertos e instituciones de los países en desarrollo.
El propósito de este trabajo es mostrar los problemas que hay para
mejorar las prácticas y reducir la probabilidad de aceptar malos
proyectos. Así mismo, evitar subestimaciones de las tarifas que se
deben cobrar por servicios de infraestructura.
Están en juego enormes sumas de dinero que se entregan a los países en
desarrollo apoyados en evaluaciones que pueden favorecer proyectos
inconvenientes. Estas posibles decisiones equivocadas van en
detrimento de los países en desarrollo.
03/02/2012
Ignacio Vélez Pareja
44