4.4.2 Hidrología El presente capítulo tiene como objetivo conocer la

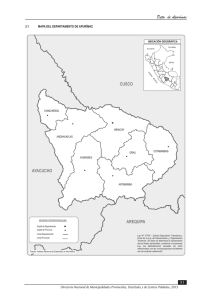
Plan de Manejo Ambiental del Proyecto
“Línea de Transmisión Machupicchu – Abancay – Cotaruse a 220 kV”
4.4.2
Hidrología
El presente capítulo tiene como objetivo conocer la disponibilidad hídrica superficial de la
zona de estudio que comprende el trazo de la línea de transmisión; asimismo, caracterizar
la geomorfología de las cuencas que involucran dicho trazo (ver el Mapa de subcuencas
hidrográficas CSL-112900-1-HI-01).
A.
Hidrología regional
La Línea de Transmisión en 220 kV Machupicchu - Abancay - Cotaruse, regionalmente, de
acuerdo a la clasificación de la Autoridad Nacional del Agua ANA, se encuentra en dos
grandes cuencas: la intercuenca del Alto Apurímac y la cuenca del río Urubamba, ambas
pertenecientes a la vertiente del Amazonas.
El río Urubamba tiene una longitud aprox. de 862 km, y es el más importante tanto por el
volumen de sus aguas como por la magnitud de su valle. Nace en los deshielos del
nevado Cunurana a 5443 m.s.n.m. al noroeste del pueblo de Santa Rosa, y con el nombre
de río Vilcanota atraviesa la alta meseta de Quequepampa y se dirige hacia el noroeste
por un valle muy poblado con localidades como Marangani, Sicuani, Combapata, entre
otras. Luego recibe las aguas del río Salcca y, al pasar por la ciudad de Urubamba, toma
el nombre de río Urubamba, hasta su confluencia con el río Tambo. El río Urubamba, en
su sector interandino, corre por un lecho con fuerte pendiente lo que origina que sus
aguas se desplacen a gran velocidad. El valle que forma es estrecho y su ensanchamiento
se produce cuando el río penetra a la Selva alta. Grandes cañones fluviales, como el que
se observa en la zona de Machupicchu, alternan con valles amplios a lo largo del río
Urubamba, hasta concluir con el imponente pongo de Mainique, donde el lecho fluvial que
se angosta considerablemente genera una ruptura de pendiente. El valle que forma el río
Urubamba y sus afluentes en la Selva alta, aguas arriba del pongo de Mainique, es
conocido con el nombre de valle de La Convención. Finalmente, el río Urubamba entrega
sus aguas al Tambo, a la altura de la localidad de Atalaya, para dar origen al río Ucayali,
en la región del mismo nombre.
Por otro lado, el río Apurímac tiene sus nacientes al norte del pueblo de Chivay, provincia
de Caylloma, región Arequipa, en el sector conocido como cordillera de Chila, en el
nevado de Mismi a 5597 m.s.n.m. Nace en pequeñas lagunas glaciares del nevado Mismi,
con el nombre de quebrada Carhuasanta. Toma una dirección sur-norte y cambia su
denominación por la de río Orcuyo. Discurre por una alta meseta, formando pequeños
meandros; recibe las aguas de la quebrada Quinchohuayco, y, a partir de entonces, se
denomina río Monigote, hasta confluir con el ramal que viene desde la zona de Caylloma,
lugar desde donde se llama río Apurímac, y que, después de atravesar elevadas mesetas
de las provincias de Caylloma, Espinar y Canas, comienza a profundizar su lecho,
tomando un rumbo general de Este a Oeste, al sur del pueblo de Paruro, hasta confluir
con el río Santo Tomás, el mismo que le da sus aguas por la margen izquierda. A partir de
entonces sigue una dirección sureste-noroeste, sirviendo de límite a los departamentos de
Apurímac y Cuzco, y formando un importante cañón que ha excavado en la antigua
meseta andina. Luego recibe las aguas del río Pampas y, a partir de esa confluencia, el río
Apurímac sirve de límite al departamento de Cuzco con Ayacucho y penetra a la Selva
alta, originando siempre un valle profundo y encajonado.
INFORME FINAL REV 0
CSL-112900-IT-11-01
CESEL Ingenieros
Setiembre 2013
Plan de Manejo Ambiental del Proyecto
“Línea de Transmisión Machupicchu – Abancay – Cotaruse a 220 kV”
B.
Hidrología local
El trazo de la línea de transmisión, en su recorrido atraviesa por las subcuencas Vilcanota
y Santa Teresa, las cuales forman parte de la cuenca del río Urubamba, y por las
subcuencas Apurímac y Chalhuanca, correspondientes a la intercuenca Alto Apurímac,
todas pertenecientes a la vertiente del Amazonas.
En la cuenca del río Urubamba se halla la subcuenca del río Vilcanota; este río se une con
el río Ahobamba a la altura de la C.H. Machupicchu, a 1800 m.s.n.m. El trazo de la línea
de transmisión atraviesa esta subcuenca hasta el vértice VMS-05, a 2550 m.s.n.m. aprox.
para luego ingresar a la subcuenca del río Santa Teresa que tiene como afluente principal
al río Sacsara, hasta llegar a los 4600 m.s.n.m. más o menos, entre los vértices VSA32 y
VSA33. Luego atraviesa la subcuenca Apurímac y cruza el río del mismo nombre en una
zona donde recibe los aportes de importantes quebradas, llega casi a los 4100 m.s.n.m.,
luego del vértice VAC-08. A continuación, la L.T. ingresa a la subcuenca del río
Pachachaca, en donde se emplaza la ciudad de Abancay, terminando su recorrido en la
subestación Cotaruse a 4100 m.s.n.m.
La subcuenca Apurímac tiene como principales afluentes al río Lambrama, la quebrada
Sojos, Huauja, y los ríos: Silcon, Accomayo, Pichirhua y Supalla.
El río Pachachaca nace al sur de la región Apurímac, en el cerro Chucchurana (4712
m.s.n.m.), con el nombre de río Collpa. Luego se denomina río Cotaruse, hasta pasar por
la ciudad de Chalhuanca, donde toma la denominación de este centro poblado, hasta
confluir con el río Antabamba que llega por su margen derecha, lugar en donde recibe la
denominación de río Pachachaca, nombre que conserva hasta dar sus aguas al río
Apurímac, cerca de la desembocadura del río Pampas. En su recorrido drena grandes
áreas de la región Apurímac, y en su valle existen varios centros poblados.
Aproximadamente, a partir del vértice VAC-05A, la línea de transmisión se ubica paralelo
al río Pachachaca hasta el vértice VAC-12B, para después encontrarse esta vez con el río
Cotaruse, cerca al vértice VAC-17N, y recorrer paralela a esta hasta su nacimiento,
cercano al vértice VAC-20N; luego la línea de transmisión sigue su recorrido en dirección
suroeste, hasta cruzarse con el río Jacultamayoc, y a poco más de un (01) km termina su
recorrido en la subestación Cotaruse.
INFORME FINAL REV 0
CSL-112900-IT-11-01
CESEL Ingenieros
Setiembre 2013
Plan de Manejo Ambiental del Proyecto
“Línea de Transmisión Machupicchu – Abancay – Cotaruse a 220 kV”
Figura 4.4.2-1
Cuencas del área de estudio
Fuente: elaborado por CESEL S.A.
INFORME FINAL REV 0
CSL-112900-IT-11-01
CESEL Ingenieros
Setiembre 2013
Plan de Manejo Ambiental del Proyecto
“Línea de Transmisión Machupicchu – Abancay – Cotaruse a 220 kV”
Figura 4.4.2-2
Diagrama topológico
Fuente: elaborado por CESEL S.A.
INFORME FINAL REV 0
CSL-112900-IT-11-01
CESEL Ingenieros
Setiembre 2013
Plan de Manejo Ambiental del Proyecto
“Línea de Transmisión Machupicchu – Abancay – Cotaruse a 220 kV”
C.
Características de las subcuencas
Subcuenca del río Vilcanota
La subcuenca del río Vilcanota está ubicada en las provincias de Urubamba, Anta,
Cusco, Acomayo, Canchis, Quispicanchi y Paucartambo, en el departamento de
Cusco.
Esta subcuenca delimitada hasta la confluencia con el río Ahobamba, aprox. por
2
donde cruza la línea de transmisión; tiene un área de drenaje de 9359,7 km y un
perímetro de 784,4 km.
Subcuenca del río Santa Teresa
La subcuenca del río Santa Teresa, delimitada hasta su confluencia con el río
2
Vilcanota, tiene un área de drenaje de 372,9 km y un perímetro de 103,2 km,
localizándose en el departamento de Cusco, provincia de La Convención.
Drena sus aguas al río del mismo nombre y recibe los aportes, por la margen derecha,
de quebradas como Totorayoc y Humantay.
Subcuenca del río Apurímac
La subcuenca del río Apurímac, delimitada hasta pocos metros aguas abajo del cruce
2
con la línea de transmisión, tiene un área de drenaje de 24 367,2 km y un perímetro
de 972,3 km. En su recorrido cruza los departamentos de Cusco y Apurímac en las
provincias de Anta, Abancay, Grau, Cotabambas, Paruro, Cusco, Antabamba,
Chumbivilcas, Espinar y Condesuyos.
Subcuenca del río Pachachaca
La subcuenca del río Pachachaca drena sus aguas hacia el río del mismo nombre, el
cual tiene sus orígenes como río Cotaruse. Está ubicada en el departamento de
Apurímac, en las provincias de Abancay, Antabamba y Aymaraes.
A su vez, la subcuenca delimitada hasta la confluencia con el río Tincoc, aprox. a 16
km, aguas abajo del cruce del río Pachachaca con la línea de transmisión, posee un
2
área de drenaje de 7577,4 km y un perímetro de 577 km.
El mapa CSL-112900-1-HI-01 muestra las subcuencas comprendidas en el área de
estudio.
En el siguiente cuadro se resume las principales características de las subcuencas.
INFORME FINAL REV 0
CSL-112900-IT-11-01
CESEL Ingenieros
Setiembre 2013
Plan de Manejo Ambiental del Proyecto
“Línea de Transmisión Machupicchu – Abancay – Cotaruse a 220 kV”
Cuadro 4.4.2-1
Características físicas de las cuencas
Subcuenca
Área
2
(km )
Perímetro
(km)
Vilcanota
Santa Teresa
Apurímac
Pachachaca
9359,7
372,9
24367,2
7577,4
784,4
103,2
972,3
577
Longitud
de río
(km)
330
35,6
379,9
181,5
Pendiente
(m/m)
0,01
0,1
0,01
0,02
Cota
mayor
(m.s.n.m.)
4850
5200
5150
5200
Cota
menor
(m.s.n.m.)
1800
1550
1650
1700
Fuente: elaborado por CESEL S.A.
D.
Análisis de consistencia de datos
Se utiliza para determinar si los registros históricos disponibles son confiables, mediante
procesos físicos y estadísticos que permiten identificar, evaluar, y eliminar los posibles
errores sistemáticos que pudieron ocurrir.
Los registros pluviométricos pertenecen a las estaciones mostradas en el siguiente
cuadro.
Cuadro 4.4.2-2
Ubicación de estaciones con información pluviométrica
Ubicación
Altitud
(m.s.n.m.)
Abancay
Lat. 13º 36’ S
Long. 72º 52’ W
2750
Chalhuanca
Lat. 14º 23’ S
Long. 73º 10’ W
3358
Estación
Machupicchu
Curahuasi
Granja Kayra
Lat. 13º 10’ S
Long. 72º 32’ W
Lat. 13º 33’ S
Long. 72º 44’ W
Lat. 13º 33’ S
Long. 71º 52’ W
Periodo de
registro
19972010,2012
Parámetro
Precipitación total mensual
Precipitación total mensual
2000 - 2012
Precipitación máx. en 24 h
2563
1999 - 2012
Precipitación total mensual
2763
1984 - 2008
Precipitación máx. en 24 h
3219
1983 - 2001
Precipitación máx. en 24 h
Fuente: SENAMHI.

Análisis visual gráfico
Se utiliza para analizar la tendencia de los registros históricos con el fin de
determinar si existen saltos dentro de un periodo registrado.
INFORME FINAL REV 0
CSL-112900-IT-11-01
CESEL Ingenieros
Setiembre 2013
Plan de Manejo Ambiental del Proyecto
“Línea de Transmisión Machupicchu – Abancay – Cotaruse a 220 kV”
Figura 4.4.2-3
Análisis gráfico de las estaciones meteorológicas
3000
2500
Precipitación (mm)
2000
1500
1000
500
0
1998
2000
2002
2004
2006
2008
2010
Años
Abancay
Chalhuanca
Macchupicchu
Fuente: elaborado por CESEL S.A, en base a información proporcionada por SENAMHI.
En el gráfico no se observan saltos significativos en los datos anuales de
precipitación de las estaciones analizadas.

Análisis doble masa
Este método es utilizado para verificar la homogeneidad de los datos en una
estación pluviométrica.
El diagrama de doble masa se obtiene graficando en el eje de las abscisas los
acumulados de las precipitaciones de todas las estaciones, y en el eje de las
ordenadas, los acumulados de cada estación.
INFORME FINAL REV 0
CSL-112900-IT-11-01
CESEL Ingenieros
Setiembre 2013
Plan de Manejo Ambiental del Proyecto
“Línea de Transmisión Machupicchu – Abancay – Cotaruse a 220 kV”
Figura 4.4.2-4
Diagrama doble masa
Precipitación Acumulada por Estación
25000
20000
15000
10000
5000
0
0
2000
4000
6000
8000
10000
12000
14000
16000
Precipitación Promedio Acumulado Total
ABANCAY
CHALHUANCA
MACCHUPICCHU
Fuente: elaborado por CESEL S.A., en base a información proporcionada por SENAMHI.
En el gráfico anterior se puede observar que la distribución de los datos de las
estaciones no sufre cambios de pendiente; por lo tanto, de acuerdo a los
análisis anteriores, los datos son homogéneos y no necesitan corrección.
E.
Caudales medios
Las variaciones de caudal definen el régimen hidrológico de un río; a su vez, las
variaciones temporales súbitas se dan durante o después de las tormentas.
Así mismo, los ríos y quebradas presentan variaciones en su caudal, tanto más
acentuadas cuando más pequeña es la cuenca colectora.
Para la estimación de los caudales medios en las subcuencas del área de estudio, se
utilizó el método del número de curva o SCS.
a. Método del SCS para abstracciones
Este método se sustenta en la relación precipitación-escorrentía y en las
características de los suelos de la cuenca en estudio, desde el punto de vista
hidrológico, esto es su mayor o menor retención del agua precipitada antes de que
se produzca la escorrentía, considerando el tipo de cobertura (cultivos, pastizales
o praderas y bosques), el tipo de suelo (arena, gravas, limos y arcillas), su
profundidad y la morfología del área de la cuenca.
El método SCS consiste en:

INFORME FINAL REV 0
CSL-112900-IT-11-01
Seleccionar para la cuenca una de las curvas de escorrentía CN (un número
en una escala de cero a cien) que refleje las características hidrológicas de los
suelos de la cuenca en estudio
CESEL Ingenieros
Setiembre 2013
Plan de Manejo Ambiental del Proyecto
“Línea de Transmisión Machupicchu – Abancay – Cotaruse a 220 kV”

Hallar la lámina de escorrentía directa que es de esperar ocurra en la cuenca
de estudio después de una intensa y prolongada precipitación.

Estimación de la escorrentía directa
La abstracción inicial (Ia) es igual a la precipitación acumulada antes que
comience el escurrimiento; físicamente, la comprende la interceptación, el
almacenamiento y la infiltración. Según datos de cuencas medidas:
I a  0,2S
Dónde:
S: es la infiltración potencial máxima.
El escurrimiento real está dado por la siguiente expresión:
Pe 
( P  0,2S ) 2
P  0,8S
Dónde:
Pe: es la escorrentía real en mm
P: es la precipitación en mm
S: es la infiltración potencial.
Los números de las curvas que caracterizan a los suelos desde el aspecto
hidrológico, se relacionan con S de acuerdo a la siguiente igualdad:
CN 
1000
10  S
Despejando S:
S
1000
 10
CN
Siendo:
S: la infiltración potencial en pulgadas
CN: el número de la curva.

Selección del valor de la curva (CN)
El siguiente cuadro muestra los distintos valores de número de curva de
escorrentía para las diferentes coberturas.
INFORME FINAL REV 0
CSL-112900-IT-11-01
CESEL Ingenieros
Setiembre 2013
Plan de Manejo Ambiental del Proyecto
“Línea de Transmisión Machupicchu – Abancay – Cotaruse a 220 kV”
Cuadro 4.4.2-3
Número de curva de escorrentía
Número de curva para grupos de
suelos hidrológicos
A
B
C
D
Descripción y tipo de cobertura
Condición
hidrológica
Pastos, forraje para pastoreo
Mala
Regular
Buena
68
49
39
79
69
61
86
79
74
89
84
80
Prados continuos, protegidos de pastoreo, y
generalmente segado para heno
----
30
58
71
78
Mala
Regular
Buena
Mala
Regular
Buena
Mala
Regular
Buena
48
35
30
57
43
32
45
36
30
67
56
48
73
65
58
66
60
55
77
70
65
82
76
72
77
73
70
83
77
73
86
82
79
83
79
77
---
59
74
82
86
Maleza mezclada con pasto de semilla, con la
maleza como principal elemento
Combinación de bosques y pastos (huertas o
granjas con árboles)
Bosques
Predios de granjas, construcciones, veredas,
caminos y lotes circundantes
Fuente: Soil Conservation Service

Estimación del caudal medio mensual
El caudal medio mensual se calcula a partir de la información pluviométrica
total mensual y de la elección de la curva (CN), y que como se ha indicado
caracteriza a los suelos desde el aspecto hidrológico.
A su vez, el caudal en un mes dado “i” no solo es dependiente de la
precipitación pluvial ocurrida en el mes “i”, sino también de la precipitación
ocurrida en el mes anterior “i–1”; por lo que se considera que la precipitación
efectiva (Pe), que genera la escorrentía, obedece a la siguiente expresión:
Pei  0,4Pi1  0,6Pi
Dónde:
Pei: precipitación efectiva en el mes considerado en mm
Pi – 1: precipitación ocurrida en el mes anterior en mm
Pi :
precipitación del mes actual en mm.
Para obtener las series de precipitación que originan la escorrentía en las cuencas
comprendidas en el área de estudio, se consideró la ecuación para los registros
de las estaciones representativas.
Finalmente, el caudal medio mensual se determina multiplicando la precipitación
efectiva en el mes considerado por el área de la cuenca:
Qm  Pei x A
INFORME FINAL REV 0
CSL-112900-IT-11-01
CESEL Ingenieros
Setiembre 2013
Plan de Manejo Ambiental del Proyecto
“Línea de Transmisión Machupicchu – Abancay – Cotaruse a 220 kV”
b. Determinación de los caudales medios
En el siguiente cuadro se indica las descargas medias mensuales estimadas para
las subcuencas comprendidas en el área de estudio, y en el gráfico, la variación
mensual de las mismas.
Cuadro 4.4.2-4
3
Caudales medios mensuales (m /s)
Subcuenca
ENE.
FEB.
MAR. ABR. MAY. JUN.
JUL. AGO. SEP.
OCT. NOV.
DIC.
Promedio
Vilcanota
773,5
905,7
846,4
584,2
161,4
34,8
29,9
29,2
51,6
188,7
298,9
476,5
365,1
Santa Teresa
30,8
36,1
33,7
23,3
6,4
1,4
1,2
1,2
2,1
7,5
11,9
19,0
14,5
Apurímac
827,6
1083,3
786,7
287,6
14,7
3,9
3,2
0,5
0,9
71,5
153,7
433,3
305,6
Pachachaca
246,2
369,0
304,4
131,9
5,6
3,5
0,2
0,0
0,1
9,0
17,0
86,8
97,8
Fuente: elaborado por CESEL S.A. en base a datos de SENAMHI.
Figura 4.4.2-5
3
Caudales medios mensuales estimados en las subcuencas (m /s)
Fuente: elaborado por CESEL S.A. en base a datos de SENAMHI.
F.
Descargas máximas
Los caudales máximos (avenidas) producidos por la escorrentía superficial se han
determinado mediante la metodología del hidrograma unitario del ex Soil Conservation
Service de los Estados Unidos (SCS).
a. Descripción del método SCS o método del número de curva
El método SCS o del Número de Curva (CN), del U.S. Soil Conservation Service,
fue desarrollado en 1982, inicialmente, para estimar avenidas e hidrogramas de
avenidas de cuencas pequeñas. Desarrollos posteriores permitieron aplicarlo a
cuencas mayores, al incorporar los efectos del almacenamiento del cauce.
Cabe señalar que el nombre del método deriva de una serie de curvas, cada una
de las cuales lleva el número N (o CN) que varía desde 1 hasta 100. Un número
INFORME FINAL REV 0
CSL-112900-IT-11-01
CESEL Ingenieros
Setiembre 2013
Plan de Manejo Ambiental del Proyecto
“Línea de Transmisión Machupicchu – Abancay – Cotaruse a 220 kV”
de curva N = 100 indica que toda la lluvia escurre, y un número N = 1 significa que
toda la lluvia se infiltra; por lo que los números de curvas representan coeficientes
de escorrentía.
Por otro lado, el método se desarrolló utilizando datos de un gran número de
cuencas experimentales, y se basa en la siguiente relación:
F Q
…(1)

S Pe
Dónde:
F:
S:
Q:
Pe:
infiltración real acumulada (mm)
infiltración potencial máx. (mm)
escorrentía total acumulada (mm)
escorrentía potencial o exceso de precipitación (mm).
La ecuación (1) se considera válida a partir del inicio de la escorrentía, donde Pe
se define como:
Pe  P  I a …(2)
Mientras que F es definida de la siguiente forma:
F  Pe  Q …(3)
El término Ia (abstracciones iniciales) es definido como la precipitación acumulada
hasta el inicio de la escorrentía, y es una función de la intercepción,
almacenamiento en depresiones e infiltración antes del comienzo de la
escorrentía.
Haciendo las sustituciones respectivas, y considerando la relación establecida por
datos experimentales: Ia = 0,2 S, se presenta la ecuación principal del método:
Q
( P  0,2S ) 2
… (4)
P  0,8S
Cabe precisar que debe tenerse presente que en esta ecuación, P y S deben
tener las mismas unidades, y el Q obtenido también tendrá las mismas unidades.
El SCS, después de estudiar un gran número de pequeñas cuencas, estableció
una relación para estimar S a partir del número de curva N o CN, mediante la
ecuación que, finalmente, tiene la expresión:
S
INFORME FINAL REV 0
CSL-112900-IT-11-01
1000
 10 … (5)
CN
CESEL Ingenieros
Setiembre 2013
Plan de Manejo Ambiental del Proyecto
“Línea de Transmisión Machupicchu – Abancay – Cotaruse a 220 kV”
Donde la infiltración potencial máx. está expresada en pulg., y haciendo las
transformaciones se tiene:
 100 
S  254 
 1 (en mm)
 CN 

Determinación del hidrograma unitario triangular sintético
Este método consiste en estimar un hidrograma triangular unitario sintético, a
partir de las características físicas de la cuenca y un perfil de precipitación
efectiva, las cuales convergen para producir un hidrograma compuesto de la
avenida.
La geometría del hidrograma unitario se muestra a continuación:
Del gráfico anterior se tiene que el caudal máx. es:
Qp 
2A
… (6)
Tb
Para un milímetro de lluvia efectiva el caudal pico resulta igual a:
Qp 
0,208 A
… (7)
TP
Dónde:
Qp:
A:
Tp:
3
caudal pico por milímetro de lluvia efectiva en m /s
2
área de drenaje en km
tiempo de ocurrencia del pico del hidrograma unitario triangular en
horas.
Además:
Tp 
INFORME FINAL REV 0
CSL-112900-IT-11-01
de
t p … (8)
2
CESEL Ingenieros
Setiembre 2013
Plan de Manejo Ambiental del Proyecto
“Línea de Transmisión Machupicchu – Abancay – Cotaruse a 220 kV”
Dónde:
de: duración de la lluvia en exceso, en horas.
tp: tiempo de retardo, el cual se estima mediante el tiempo de concentración en
horas.
El tiempo de concentración se determina de acuerdo a la fórmula de Kirpich:
TC  0,000325
L0.77
S 0.385
… (9)
Dónde:
Tc:
L:
S:
tiempo de concentración en horas
longitud del curso principal en metros
pendiente del cauce principal en m/m.
Finalmente, el caudal de avenidas se obtiene multiplicando el caudal unitario por la
altura de lluvia efectiva, la cual ha sido calculada a partir de la precipitación
máxima en 24 h para un tiempo de retorno de 500 años.
El estudio de avenidas tiene por finalidad determinar la intensidad de la
precipitación para un periodo de retorno de 500 años que servirá para obtener los
caudales de diseño de las obras de manejo de agua; para ello se utilizó la
información de la precipitación máxima en 24 h de las estaciones más cercanas a
la zona del proyecto. Para el análisis se considera las distribuciones estadísticas
como: Normal, Log normal, Log Pearson III y Gumbel; y mediante la Prueba de
Bondad de Ajuste de Kolmogorov-Smirnov, se determina la que mejor se ajusta a
los registros.
Las estaciones meteorológicas analizadas son: Chalhuanca, Curahuasi y Granja
Kayra.

Prueba de Bondad de Ajuste Kolmogorov - Smirnov
Permite determinar la distribución estadística que más se ajusta a los registros de
precipitación. Consiste en comparar el máximo valor absoluto de la diferencia ∆
entre la función de distribución de probabilidad observada F o (Xm) y la estimada
por cada función F(Xm).
  máx F0 ( X m )  F ( X m )
La función de probabilidad observada se calcula como:
Fo( Xm)  1 
m
n 1
Dónde:
INFORME FINAL REV 0
CSL-112900-IT-11-01
CESEL Ingenieros
Setiembre 2013
Plan de Manejo Ambiental del Proyecto
“Línea de Transmisión Machupicchu – Abancay – Cotaruse a 220 kV”
m:
n:
es el número de orden del dato Xm en una lista de mayor a menor
es el número total de datos.
b. Cálculo de descargas máximas
El análisis de las descargas máximas se ha elaborado basándose en los registros
de precipitación procedentes de las estaciones Chalhuanca, Curahuasi y Granja
Kayra, debido a que cuenta con un amplio período de registro, además de ser las
más representativas para el objetivo del estudio. El registro de la precipitación
máxima se encuentra en el anexo 4.4.2-A Información histórica de precipitación
máxima en 24 h.
La precipitación máxima en 24 h de dichas estaciones fue ajustada para el análisis
de caudales máximos, por un factor que es el cociente de la relación entre la
precipitación total anual a una altitud media de cada subcuenca y la precipitación
total media anual de la estación.
Cuadro 4.4.2-6
Precipitaciones máximas con factor
Año
1983
1984
1985
1986
1987
1988
1989
1990
1991
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
2002
2003
2004
2005
2006
2007
2008
2009
2010
24,28
41,41
35,39
31,20
47,76
39,93
47,53
30,06
42,65
28,59
Subcuenca
Santa
Teresa
23,12
39,43
33,71
29,71
45,48
38,03
45,27
28,63
40,62
27,22
44,92
39,25
35,51
53,32
40,73
21,89
28,93
32,56
42,78
37,38
33,81
50,78
38,78
20,85
27,55
31,01
Subcuenca
Vilcanota
Subcuenca
Apurímac
26,83
20,84
21,85
28,66
31,31
3,05
11,89
25,72
17,48
36,08
45,74
55,80
26,43
33,75
23,28
28,56
29,68
26,63
35,47
60,58
23,99
30,09
30,29
28,05
27,54
Subcuenca
Pachachaca
28,25
41,77
29,65
34,16
41,07
28,05
56,50
38,67
50,69
25,54
39,57
Fuente: elaborado por CESEL S.A. en base a datos de SENAMHI.
INFORME FINAL REV 0
CSL-112900-IT-11-01
CESEL Ingenieros
Setiembre 2013
Plan de Manejo Ambiental del Proyecto
“Línea de Transmisión Machupicchu – Abancay – Cotaruse a 220 kV”
Con los datos procesados de precipitaciones máx. y mediante la prueba de
Bondad de Ajuste de Kolmogorov-Smirnov, se tiene la distribución que mejor se
ajusta.
Cuadro 4.4.2-7
Resultados - Prueba de Bondad de Ajuste Kolmogorov-Smirnov
Subcuenca
Máximo valor
absoluto
Distribución
Vilcanota
0,0768
Normal
Santa Teresa
0,0768
Normal
Apurímac
0,1350
Gumbel
Pachachaca
0,1250
Normal
Fuente: elaborado por CESEL S.A.
De los resultados se observa que la distribución probabilística Normal es la que
mejor se ajusta a los registros. En el siguiente cuadro se muestra las
precipitaciones máx. para un tiempo de retorno de 500 años.
Cuadro 4.4.2-8
Precipitaciones máximas por subcuenca
(TR = 500 años)
Subcuenca
Precipitación máx. (mm)
Vilcanota
61,8
Santa Teresa
58,9
Apurímac
81,7
Pachachaca
65,9
Fuente: elaborado por CESEL S.A. en base a datos de SENAMHI.
Cuadro 4.4.2-9
Descargas máximas (TR=500 años)
Subcuenca
Vilcanota
Santa
Teresa
Apurímac
Área
(km2)
Longitud
del
cauce
(km)
Pendiente
(m/m)
Curva
Número
CN
Tiempo de
Concentración
tc (hr)
Tiempo
de
retardo
tp (hr)
Tiempo
Pico
Tp (hr)
Altura
de
Lluvia
P
(mm)
Retención
de
la cuenca
S (mm)
Lluvia
Efectiva
Pe
(mm)
Caudal
Máximo
Qp
(m3/s)
9359,7
330
0,01
70
34,0
20,38
37,37
61,8
108,86
10,78
561,61
372,9
35,6
0,1
70
2,52
1,51
2,77
58,9
108,86
9,44
264,04
24367,20
379,9
0,01
75
37,9
22,72
41,65
81,7
84,67
28,05
3413,41
9,85
18,06
65,9
67,52
22,87
1995,61
181,5
0,02
79
16,4
Pachachaca 7577,4
Fuente: elaborado por CESEL en base a datos de SENAMHI.
INFORME FINAL REV 0
CSL-112900-IT-11-01
CESEL Ingenieros
Setiembre 2013