Ángulos en posición normal o en posición estándar

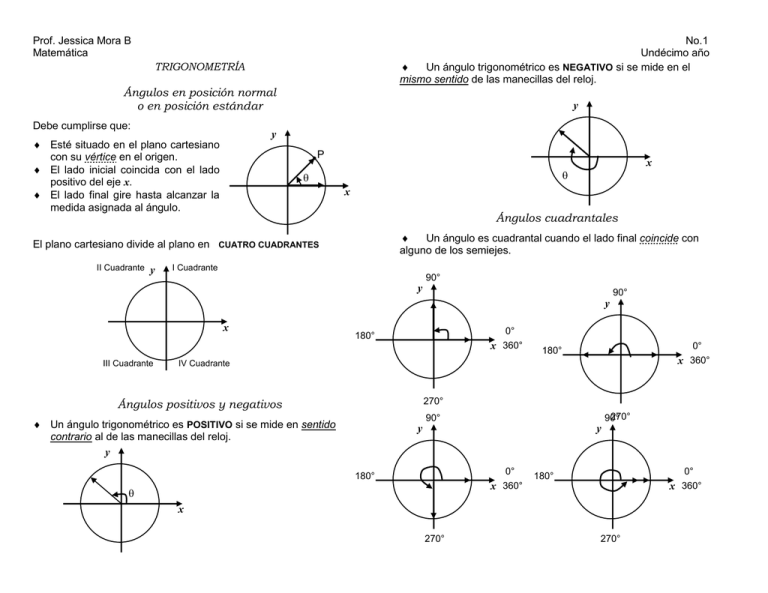
Prof. Jessica Mora B
Matemática
No.1
Undécimo año

Un ángulo trigonométrico es NEGATIVO si se mide en el
mismo sentido de las manecillas del reloj.
TRIGONOMETRÍA
Ángulos en posición normal
o en posición estándar
Debe cumplirse que:
y
y
 Esté situado en el plano cartesiano
con su vértice en el origen.
 El lado inicial coincida con el lado
positivo del eje x.
 El lado final gire hasta alcanzar la
medida asignada al ángulo.
P


x
Ángulos cuadrantales

Un ángulo es cuadrantal cuando el lado final coincide con
alguno de los semiejes.
El plano cartesiano divide al plano en CUATRO CUADRANTES
II Cuadrante
y
x
I Cuadrante
90°
y
90°
y
x
0°
180°
x 360°
III Cuadrante
0°
180°
x 360°
IV Cuadrante
Ángulos positivos y negativos
270°
270°
90°
90°
 Un ángulo trigonométrico es POSITIVO si se mide en sentido
contrario al de las manecillas del reloj.
y
y
y
0°
x 360°
180°

0°
x 360°
180°
x
270°
270°
Prof. Jessica Mora B
Matemática
No.2
Undécimo año
Conversión de ángulos de grados a Radianes y viceversa
 El radián es una medida angular.
1. Realice la conversión a Radianes de los siguientes ángulos
 Un ángulo tiene una medida de 1 radián si al colocar su vértice en
el centro de un círculo, la longitud del arco interceptado en la
 2 radianes
( a ) 45°
( d ) 140° ( g ) – 20° ( j ) 740°
( m ) – 5°
( b ) – 132° (e) – 570° ( h ) 311° (k)– 2280° ( n )
( c ) 90°
circunferencia es igual al radio del círculo.
 1 radián
Práctica
( f ) 210° ( i ) 360° ( l ) 120°
8°
( ñ ) 190°
 3 radianes
2. Realice la conversión a Grados de los siguientes ángulos
(a) 5
(d) π
π
(e)7
(b) –
(c)
4
8π
5
 Entonces para cambiar de Grados a radianes y viceversa se utiliza
la siguiente fórmula:
Grados Radianes

180 
π
Por ejemplo:
2. A cuánto equivale 3
Grados 3 π

180 
π
72 
π  Radianes
180 
2
π  Radianes
5

en grados.
Grados 
π
( j ) – 5π
2
(m)– 11π
3π
(h)
4
(k)
5π
3
(n)
17 π
(i )
3
(l) –
7π
6
(ñ) –
π
3
9π
2
Ángulos coterminales
 Los ángulos coterminales son aquellos ángulos que tienen los
mismos lados iniciales y terminales.
 Los ángulos coterminales se pueden obtener SUMANDO al
1. A cuánto equivale 72 ° en radianes.
72 
Radianes

180 
π
( f ) 21
(g)–
3π
π
ángulo dado 360°n veces o bien RESTANDO al ángulo dado 360°
n veces.
Por ejemplo:
a. Un ángulo coterminal a 52° podría ser 772° , pues se le
sumó al ángulo dado 360° dos veces, que equivale a decir que
180
dio dos vueltas más en contra de las manecillas del reloj.
Así 772° = 52° + 360° + 360°
Grados 540 
o bien,
Prof. Jessica Mora B
Matemática
b. Un ángulo coterminal a 52° podría ser – 1028° , pues se le restó
Signos de las Funciones trigonométricas
al ángulo dado 360° tres veces, que equivale a decir que dio tres
de cualquier ángulo
vueltas más a favor de las manecillas del reloj.
Así – 1028° = 52° – 360° – 360° – 360°
PRÁCTICA
1. Indique a qué cuadrante pertenece cada uno de los siguientes
ángulos. Si es un ángulo cuadrantal indíquelo. (Sugerencia:
ubique el ángulo dibujándolo primero)
( c ) 480°
( d ) – 150°
( f ) – 130°
( g ) –180°
( h ) – 25°
( i ) 900°
(j ) – 360°
( k ) 1840°
( m ) – 35°
( n ) – 271°
( ñ ) –240°
( o ) 720°
( p ) 110°
(q)
( r ) 215°
( s ) 721°
( t ) – 4
(u) –
(a)
270°
( b)
(e)
16°
(x) –
9π
4
1°
180°
3
π
5
7π
(y)–
2
(v ) 15
(z)
7π
6
( l ) – 90°
( w ) 10
( aa )
π
3
( ab ) 6
2. Encuentre un ángulo coterminal positivo y uno negativo para
los ángulos del ejercicio anterior.
No.3
Undécimo año
Recordemos que el plano cartesiano está compuesto por cuatro
cuadrantes
y
SEN y CSC
son positivas
TODAS las funciones
son positivas
II
Cuadrante
I
Cuadrante
x
III
IV
Cuadrante Cuadrante
TAN y COT
son positivas
COS y
Práctica
1. ¿En que cuadrante termina el ángulo  si:
a. sen  y cos  son ambos negativos?
b. sen  y
tan  son ambos positivos?
c. sen  es positivo y
d. sec  y
SEC
son positivas
sec  negativo?
tan  son ambos negativos?
2. ¿En que cuadrante puede terminar el ángulo  si:
a. sen  es positivo?
b. cos  es negativo?
c. tan  es negativo?
d. sec  es positivo?
Prof. Jessica Mora B
Matemática
No.4
Undécimo año
Ej.
Angulo de referencia
a. Determine el ángulo de referencia para
Si 
es un ángulo en posición estándar y el lado final no se
encuentra sobre un semi–eje coordenado, entonces el ÁNGULO DE
REFERENCIA para  es el ÁNGULO AGUDO 1 que forma el lado
final de  en el eje x, positivo o negativo.
y
y
 
x
x
Si  es agudo entonces   
entonces  180 °
y

es obtuso
225°
2800°
 45°
133°
65°
721°
300°
278°
456°
3
7 
 
3
5
  
  
3
4
 
5
2

Cos 150°
Sen 315°
Tan –240°
Sec 225°
Cot 40°
Cos 788°
Sen  45°
Csc 98°
4

6
entonces  180 °


3
3
2
Tan =  3 
2
Cos = 



x
Sec = –
2
Csc = 2 
Si  está en el III Cuadrante
7
3
b. Calcule:
Sen  = 

x
240°
c. Determine el valor del ángulo de referencia (  ) y el
valor del ángulo original () en cada uno de los siguientes
casos.
y



Si
315°


 
150°


1

3
Cot =  3 
Si  está en el IV Cuadrante
entonces 360 °
Csc  = 
2 3
3
Tan  = 1
Cos = 
3
2

Prof. Jessica Mora B
Matemática
No.5
Undécimo año
Ecuaciones trigonométricas
Resuelva las siguientes ecuaciones en el intervalo
Circunferencia Trigonométrica
[ 0, 2 [
(1) 2 cos x  1
(10) senβ  2 senβ cosβ  0
(2) 2 sen  1  0
(11) senx tan x  senx 
 Es una circunferencia con centro en el origen y
con radio igual a una unidad (1).
y
P
1
x
(3) 2 sen2   1  0
(12) 4sen2 α tanα  tanα  0
(4) 3 sec2 x  4 tan2 x
(13) 2 sen2 A  1 cos A
(5) 3 sen x  2 cos x
(14) 2 cos   5 sen  1  0
(6) 2 cos2   3 sen   0
(15) sen x  1  2 cos2 x
 La circunferencia trigonométrica corta a los ejes
coordenados en determinados puntos:
y
2
2
(7) 2 sen x  cos x 
2
7
4
(8) cos2 δ  senδ  1  
(16) 2 tan2 x  sec2 x  2
(17) 2 cos 2  + 3 cos  = 0
(0,1)
P
(–1,0)
(0,–1)
 El punto P ubicado en la figura, tiene dos
coordenadas “x” y “y”, o sea P(x, y).
y
P ( x , y ) = P (cos  , sen )
1
(9) –2 cos x – 3 sen x = 0
2
(18) 4 cos  – cos  = 0
3
x
(1,0)

x
y
x
Prof. Jessica Mora B
Matemática

PRÁCTICA
Marque con una “x ” la opción correcta en cada uno de los casos que
a continuación se le presentan
 De acuerdo con los datos de la figura, se cumple con certeza que
( ) cos  = b
y
1
b
( ) csc  = 
a
a
( ) cot  =
b
(-a,b)

-1
( ) sen  = – a
x
1
( )
-1
( )
( )
1
1
( )
1
x
( )
-1

(
(
(
(
Si tan  es negativo, entonces el ángulo  podría encontrarse
en los cuadrantes
) III
) II
) II
) III
y
y
y
y
I
IV
I
IV
-1
1

x
-1
En la figura,  es la medida de un ángulo en posición normal,
( )–

-1

valor de tan  corresponde a
( )– 3
2
2
2
( )
y
1
2
1
(-u,v)
el cual determina un ángulo de referencia de
De acuerdo con los datos de la figura, el valor de cos  es
( )  2
1
u
u
( ) 
v
1
( ) 
u
1
( ) 
v


No.6
Undécimo año
De acuerdo con los datos de la figura, la función cot 
corresponde a
v
y

y

, entonces el
3
1
1

3
1
-1
1
3
3
x
-1
De acuerdo con los datos de la figura, el valor de 

6
7
( )
6
8
( )
6
5
( )
6
1
( )

1 x
-1

 

3
2
,
1

2
-1
es
Prof. Jessica Mora B
Matemática
No.7
Undécimo año
(5)
Relaciones pitagóricas en la Circunferencia Trigonométrica
cos x cscx

cot2 x
(6) sec 2  + csc
(7) sec  + sec  sen 2 
 Relación pitagórica principal
(9) sen   sec  cot =
y
2
(11) sen x  cos x  
1

x
(13) tan x +
cos x
1  sen x

(15) cos 2  sec 2  – 1=
(18) (1 – cos x) (1 + cos x) =
 De la relación principal obtenemos las siguientes relaciones
pitagóricas.
Ejercicios
Simplifique al máximo las siguientes expresiones trigonométricas
(3) sen
2
(20)
sen β cosβ
=

csc β sec β
(22)
sec β
=
tan β
 1 + Cot 2 = Csc 2 
Simplificación de Expresiones Trigonométricas


 + cos 2  + tan 2 


 1  cot 2 α =
(12)
(14)
1  tan2 x

csc 2 x
tan2 x - sen 2 x

tan 2 x
(16) sec
2
  cot 2  =
2
2
(17) sen x  cos x   sen x  cos x  
Sen 2 Cos 2 = 1
(1) cos   csc 
2

(10) (sec x + tan x) (1 – sen x) =
y
x
 Tan 2 1= Sec 2 
(8) sen
2

(2) csc x  tan x =
(4)
sec 2 θ

sec 2 θ - 1
(19) sec x  cot x =
(21)
cos 2 β sec β
=
senβ
(23) 1 - cos  1  sec  cot  