2. Modelo teórico. Trabajos anteriores (A. Bateman)

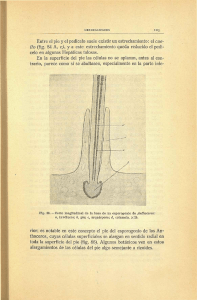
Estudio teórico-experimental de un sistema de disipación de energía poco habitual al pie de una caída de agua.
2. Modelo teórico. Trabajos anteriores (A. Bateman)
Se presenta a continuación la primera modelización del sistema en estudio:
estrechamiento tras caída. El modelo teórico asume unas ciertas hipótesis que parecen
razonables y, tras un cálculo aplicando los principios básicos de la hidráulica de
conservación de la energía y conservación de la cantidad de movimiento, permite
dimensionar el estrechamiento para un rango determinado de caudales. El esquema del
sistema es el siguiente:
yc0
H
y2
yc
∆z
y1
B
B0
Fig. 2. Esquema del modelo teórico adoptado para el sistema caída - estrechamiento - escalón.
El flujo de agua llega al pie de la caída en régimen rápido con una velocidad muy
elevada. Pasa a régimen lento a través del resalto. Dentro del estrechamiento se vuelve a
régimen rápido pero con una velocidad muy inferior a la que tenía al pie de la caída debido
a la disipación de energía que produce el resalto hidráulico. Éste es el objetivo del sistema.
La primera hipótesis de partida es que el resalto está formado, o sea, que la lámina de
agua tiene el perfil que se muestra en el esquema. Esto es importante ya que si el flujo
fuese en régimen rápido por dentro del estrechamiento y quisiéramos que se formase el
resalto deberíamos estrechar mucho más para frenar el agua ya que esta llegaría al
estrechamiento con mucha más energía precisamente porque no estaría el resalto que es lo
que disipa energía.
Conociendo el caudal Q y la altura de caída H, se puede calcular la velocidad y el
calado a pie de caída aplicando la conservación de la energía y suponiendo, para
simplificar, que las pérdidas en la caída son despreciables:
1
Estudio teórico-experimental de un sistema de disipación de energía poco habitual al pie de una caída de agua.
-
-
-
Teniendo en cuenta que en el borde de la caída cambiará el régimen del flujo de
lento a rápido y que, por tanto, se dará el calado crítico, la energía en este punto se
puede calcular mediante la expresión:
2
E0 = y c 0
3
La energía al pie de la caída será:
E1 = E0 + H
Teniendo en cuenta que:
2
v1
Q2
E1 = y1 +
= y1 +
2
2
2g
2 gB0 y1
se puede calcular el calado y1 y a continuación la velocidad v1.
La segunda hipótesis será que el resalto se forma al pie de la caída. Por tanto, no está
nada anegado y tampoco está desplazado aguas abajo, lo que permitiría unas ciertas
pérdidas en este tramo en régimen rápido. Con esta premisa y aplicando el principio de
conservación de la cantidad de movimiento se obtiene la ecuación de Belanguer que
permite calcular el calado al final del resalto (calado conjugado de y1 ):
Fr1 =
v1
gy1
;
∗
y2 = y1 =
y1
2
( 1 + 8Fr −1)
2
1
Cabe destacar que el valor calculado del calado a la entrada del estrechamiento y2 solo
depende del caudal y de la altura de la caída y siempre que se produzca el resalto será éste.
Es, por tanto, independiente de la geometría del estrechamiento.
El estrechamiento tiene dos parámetros de ajuste: el ancho del estrechamiento B y la
altura del escalón ∆z. Esto nos permite imponer dos condiciones que deberán ser dos
caudales diferentes Qa y Qb. Así conseguiremos que el estrechamiento funcione para un
rango amplio de caudales. En el diseño de los colectores de la Fontsanta y Pont Reixat se
escogieron los caudales para un periodo de retorno de T=10 años y T=100 años
respectivamente obtenidos estadísticamente de los datos hidrológicos de la zona. Se
considera que el caudal de 10 años es el correspondiente a una avenida periódica y el
caudal de 100 años el de una avenida excepcional e improbable. De esta manera se asegura
el buen funcionamiento del disipador en condiciones extremas.
Mediante el cálculo antes expuesto a partir de Qa y Qb se obtienen y2a e y2b. De estos
datos se obtienen las energías a la entrada del estrechamiento para los dos caudales Ea y Eb
mediante la expresión:
2
2
Qa
Qb
;
Ea = y2a +
E
=
y
+
b
2b
2
2
2
2
2 gB0 y 2 a
2 gB0 y 2b
La tercera hipótesis es que el paso de régimen lento a régimen rápido dentro del
estrechamiento tiene lugar en la sección de máximo estrechamiento que coincide con el
vértice del escalón, o sea, que el calado crítico yc se da justo en este punto. Esto nos
permite calcular la energía del flujo en esta sección de control a la que llamaremos E’:
E ′ = yc +
Q2
2 gB 2 y c
2
2
Estudio teórico-experimental de un sistema de disipación de energía poco habitual al pie de una caída de agua.
teniendo en cuenta que:
 Q
yc = 
B g
2
2
3
3
 = Q
1 2


g 3B3
y sustuyendo yc en la expresión de E’:
2
2
Q3
Q3
2
Q2
2
3 Q3
E′ = 1 2 +
=
+
=
1
2
2
1
2
2
2 13 23


3
3
3
3
3
3
g B
g B
2g B
g B
 Q3 
2 gB 2  1 2 
 g3B3 


Ahora, considerando la conservación de la energía podemos escribir:
Q3
E = E ′ + ∆z
y, por tanto:
2
3 Qa 3
Ea =
+ ∆z
2 13 23
g B
2
y
3 Qb 3
Eb =
+ ∆z
2 13 23
g B
restando las dos ecuaciones:
2
 23

 Qb − Qa 3 
3

Eb − E a = 
1
2
2
g 3B3
y finalmente:
3
2
  2
 2
  Qb 3 − Qa 3  
3

B=  1

2
 g 3 (E b − E a ) 


y conociendo B:
2
3 Q
∆z = E a − 3 a 2
2 gB
Con estas dos fórmulas se puede diseñar el estrechamiento.
El análisis, más delante, de los resultados experimentales del presente estudio permitirá
comprobar la bondad de estos resultados y de las hipótesis consideradas y realizar las
precisiones que vengan al caso.
Se podrá analizar cómo afecta al comportamiento del sistema la forma del
estrechamiento ya que, con unos mismos ancho B y escalón ∆z se puede dar formas
diferentes: más angulosa o más suave, más progresiva o más brusca, etc. La forma
provocará unas mayores o menores turbulencias y pérdidas, y la aparición de ondas
cruzadas más o menos importantes en el régimen rápido de salida del estrechamiento.
3