Un criterio robusto para la medida del margen –coeficiente– de

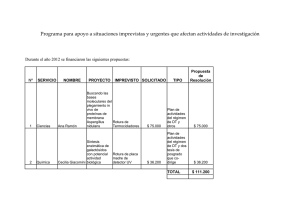
Informes de la Construcción
Vol. 62, 518, 33-42,
abril-junio 2010
ISSN: 0020-0883
eISSN: 1988-3234
doi: 10.3989/ic.08.045
Un criterio robusto para la medida del margen
–coeficiente– de seguridad
A robust approach for measuring the margin –coefficient–
of security
J. Cervera(*)
RESUMEN
SUMMARY
En este trabajo se analizan en primer lugar algunos inconvenientes de los habituales coeficientes
parciales de seguridad —factores multiplicadores de las cargas— como medida del alejamiento a las condiciones de colapso en el caso de las
estructuras con anisotropías importantes, como
son especialmente aquellas sin resistencia a la
tracción —los arcos de fábrica, como ejemplo
paradigmático— Para superar dichas dificultades
se propone un criterio sencillo y robusto basado
en la contracción de la superficie límite, criterio
que aporta una medida coincidente con la habitual para los casos isótropos, pero que permite
medir igualmente de forma consistente el alejamiento a las condiciones del colapso para el
resto de las situaciones. Se aplica finalmente el
modelo a la determinación de los márgenes de
seguridad en secciones de doble simetría sometidas a compresión esviada para materiales sin, y
con resistencia a tracción, así como al problema
de la estabilidad de un prisma frente al vuelco,
mostrando las mejoras que aporta para caracterizar dichos problemas.
This paper offers a brief analysis of the drawbacks
that can be found with the usual partial security
coefficients, as loads multipliers, when employed
for the measurement of the distance to the collapse condition in such structures, as masonry
arches, that have important anisotropies or lacks
tensile strength. To deal with such difficulties the
paper presents a simple and robust security criterium based on a contraction of the yield surface.
That criterium, that performs identically in isotropic structures to those usually employed, can
however deal consistently with situations where
former criteria fail. The criterium is applied to sections with double symmetry under axial load and
unsymmetrical bending, in materials with and
without tension resistance. It is also applied to the
prism stability problem, showing the advantages
in the caracterization of such problems.
401-11
Palabras Clave: seguridad, colapso plástico,
superficie límite, criterios de fallo, arcos de fábrica.
(*)
Keywords: security, plastic collapse, yield surface,
failure criteria, masonry arches.
Universidad Politécnica de Madrid, Madrid (España)
Persona de contacto/Corresponding author: [email protected] (J. Cervera)
Fecha de recepción: 10-12-07
Fecha de aceptación: 18-01-10
J. Cervera
1. MODELOS DE SEGURIDAD
1
1. Criterio de plastificación de Von
Mises.
Empezaremos con un breve repaso de los
modelos de seguridad al uso, para lo que
emplearemos como referencia la representación más habitual en los textos de análisis
plástico a los estados de esfuerzo, que los
identifica como un punto en el espacio cartesiano de las posibles combinaciones entre
todos ellos, y en el que los puntos correspondientes a estados de colapso están contenidos en la superficie de fluencia, siendo
los puntos interiores puntos de estado admisible para la estructura, y los exteriores
puntos que representan combinaciones de
esfuerzos inalcanzables. Un ejemplo clásico de dicha representación, para el caso
de la plastificación de un punto de un material metálico sometido a estados planos
de esfuerzo, y en el que los ejes cartesianos
representan las tensiones principales, es el
de la Figura 1, correspondiente al criterio de
resistencia de Von Mises. Hay muchas otras
referencias posibles, aunque una ya clásica
en el análisis de las estructuras de fábrica1
es (3), como lo es (5) en estructuras de hormigón.
Supondremos en lo sucesivo que la superficie se representa mediante la expresión
f(s) = 0 en la que s representa el vector que
define los esfuerzos de comprobación, y supondremos como es usual que puntos interiores a la región delimitada por f son puntos
admisibles para valores de f(s) < 0, mientras
que los puntos exteriores corresponden a
valores inalcanzables en los esfuerzos, con
f(s) > 0.
En dicha representación, obtener seguridad
frente a rotura supone asegurar que cualquiera de los estados de esfuerzo derivados
de las diversas condiciones de carga a que la
estructura va a estar sometida se sitúe suficientemente alejado de los puntos de colapso representados en dicha superficie, para
asegurar que se evita alcanzar alguno de los
casos de rotura (Figura 3).
Puede encontrarse una extensa reseña sobre los modelos de
análisis aplicados a dichas estructuras en (1).
1
Aunque usamos f(s) por mantener una cierta unidad de notación, se trata usualmente de
un caso de función agregada de
las que se denotan en el anejo
1 con F(S).
2
34
El procedimiento más clásico para establecer
un cierto grado de seguridad, asociado a los
coeficientes parciales de seguridad, trata de
alejarse de las situaciones de rotura considerando tanto reducciones en los valores de las
resistencias que representan el comportamiento del material, como ampliaciones en los valores de las cargas respecto de las realmente
existentes para establecer las que provocan la
rotura en esa estructura de material reducido,
mediante un conjunto de factores aplicados a
cada una de ellas: la rotura se supone en situaciones de carga mayorada mediante un coeficiente de seguridad que podemos denominar
mecánico y cuya determinación y calibración
habitual responde a los conocidos como mé-
todos probabilísticos de nivel 2 (2). Al objeto
de este texto no tiene inicialmente mucha importancia la diferencia de detalle en valores
entre los diferentes coeficientes, ni siquiera la
distinción entre los dos tipos de coeficiente
parcial de seguridad, por lo que podemos
imaginar el caso más sencillo para el que la
comprobación, en el formato de las normas
tradicionales, era del tipo sd ≤ f/g, formato al
que pueden reducirse en los casos lineales
las comprobaciones prescritas en la actual
normativa, ya sean del tipo:
σd (Qγf ) ≤
σd (Qγf ) ≤
f
γm
f
γm
ya sean del más completo:
“
”
E(Qγf )
” ≤ 1
ψ “ R(P
,
.
.
.
E(Qγ
)
f
m) , . . .
ψ R(P /γ
≤ 1
/γm )
donde E y R“representan respectivamente
”
) cargas
“ E(Qγ
”−
un
esfuerzo
deflas
Q1
actuanf (σ)
= ψefecto
,
.
.
.
≤0
E(Qγ
)
/γfmresistencia
)
tes
y la correspondiente
derivada
f (σ)
= ψ R(P
,
.
.
.
−
1
≤0
R(P /γm ) f
de las propiedades
en la conσd (QγPf del
) ≤material
γm
figuración estructural empleada, y donde y
representa el diagrama de interacción que
resulte de“aplicación
para ”
la combinación
E(Qγf )
ψ R(P
,
.
.
.
≤ 1 que es
de esfuerzos
considerada,
diagrama
/γm )
precisamente un caso particular de la superficie de fluencia sin más que escribir2:
f (σ) = ψ
“
E(Qγf )
,...
R(P /γm )
”
− 1 ≤ 0.
El procedimiento descrito resulta inseguro en
situaciones en las que, como en el equilibrio
de los arcos, la seguridad puede verse más
bien como un problema geométrico. Como
aclaración, en la Figura 2 se representa la
superficie límite para el plano de una junta rectangular de un arco sin resistencia en
tracción, sometido a compresiones excéntricas, y cuyos diagramas de tensiones respondan al modelo rectangular —se representa
el estado de tensiones correspondiente a diversos puntos del diagrama de fluencia—.
En el caso señalado de los arcos sin resistencia a tracción, asegurar seguridad frente
al colapso consiste habitualmente en asegurar que la resultante de las presiones correspondiente a los distintos estados de carga previstos esté contenida suficientemente
dentro de la sección, como medio de asegurar que no se produce la rótula asociada
al proceso de colapso. No se trata de un
problema de resistencia: el colapso podría
producirse aun con material de resistencia
infinita en compresión si la sección resulta
insuficiente. En este caso lo que se está haciendo implícitamente al acotar la posición
de la trayectoria de presiones es configurar
un coeficiente de seguridad geométrico que
opera en el sentido de reducir la geometría
de la sección disponible. La comprobación
Informes de la Construcción, Vol. 62, 518, 33-42, abril-junio 2010. ISSN: 0020-0883. eISSN: 1988-3234. doi: 10.3989/ic.08.045
Un criterio robusto para la medida del margen –coeficiente– de seguridad
A robust approach for measuring the margin –coefficient– of security
ahora es que la geometría considerada para
el cálculo permita el equilibrio, con gd ≤ g/g.
Puede verse un ejemplo de la aplicación de
dicha estrategia en (1). Pero dicha estrategia
no resulta suficientemente segura en el problema reseñado en los casos de cargas de
pequeña magnitud si no se combina adecuadamente dicho modelo de seguridad
con la previsión de hipótesis alternativas
de carga, hipótesis en las que se tenga en
cuenta la incertidumbre sobre su magnitud
y su posición real.
2. Superficie de fluencia en junta de
arco de fábrica.
3. Superficie límite y criterios de
seguridad en una junta de arco sin
resistencia a tracción.
4. Corrección de una situación insegura dependiente del criterio empleado.
2
Los casos citados corresponden a situaciones en las que el origen de la gráfica de
esfuerzos —o de cargas— está próximo a
una de las posibles situaciones de colapso.
En casos en los que el origen se sitúa relativamente centrado respecto de las situaciones de colapso, las estrategias anteriores
pueden considerarse intercambiables.
Una estrategia alternativa capaz de dar
adecuada cuenta de la seguridad en todas
las situaciones apuntadas consiste en establecer la seguridad mediante una reducción de la región ocupada por la superficie
límite obtenida, no por la vía de la reducción de los esfuerzos máximos, o por la vía
de la reducción de la geometría disponible,
sino por la vía de la reducción del potencial
representado por la función f(s), adoptando por tanto como superficie límite para el
cálculo la reducida f(s) + g = 0, o mediante
cualquier procedimiento análogo de contracción de la superficie de fluencia. Esta
estrategia debe implicar, para el caso que
hemos citado del equilibrio de un arco sin
resistencia a tracción, que obtener la seguridad requerida va a exigir la existencia en
cualquier caso de un nivel de carga mínimo sin el que la seguridad es inalcanzable.
En la Figura 3 vemos representados los tres
criterios de seguridad reseñados, y en la Figura 4 podemos observar con claridad la
muy diferente forma con que se aborda la
corrección de una situación límite partiendo de cada una de estas estrategias.
En la rápida aproximación anterior se han
empleado, implícitamente para no distraer
en la reflexión, algunos conceptos cuya validez se repasan de forma algo más explícita
en el anejo 1, y que resultan esenciales para
hacer aceptable la aplicación de las ideas
precedentes al caso de las fábricas.
2. UN MODELO ROBUSTO DE MEDIR EL
MARGEN DE SEGURIDAD
Por lo visto en las anteriores figuras, si el
punto de carga nula coincide con el centro de la superficie de rotura, el coeficiente
de seguridad no es más que un factor entre
dos figuras homólogas, la de rotura, y la
3
4
de comprobación empleada para el cálculo, versión homóloga y reducida en tamaño
de aquélla, siendo dicho centro el punto fijo
de la homología. Si dicho punto de carga o
esfuerzo nulo no es el centro de la superficie de rotura, debemos corregir el criterio
de comprobación de seguridad; las líneas
siguientes aportan una línea sencilla para
hacerlo.
Sea s un estado de carga —o de esfuerzo—
seguro, y sea f(s) ≤ 0 la superficie de rotura
correspondiente a las variantes posibles para
dicho estado cuyo centro —o posición de
máximo alejamiento a dicha superficie—
esté localizado en s0. El estado s correspondería a un estado de rotura en el caso de una
reducción de la superficie a una homóloga
menor, y la relación entre las dimensiones
lineales de dichas superficies puede dar la
medida del margen de seguridad correspondiente al estado s.
Informes de la Construcción, Vol. 62, 518, 33-42, abril-junio 2010. ISSN: 0020-0883. eISSN: 1988-3234. doi: 10.3989/ic.08.045
35
J. Cervera
5. Criterio robusto para medir el
margen de seguridad.
El gradiente a la superficie en el punto de rotura más próximo al punto considerado define un vector g ortogonal al plano tangente
a ésta en dicha posición de rotura. Viendo la
Figura 5, podemos considerar como margen
de seguridad, análogo al coeficiente de seguridad habitual para las cargas, al cociente
entre las proyecciones sobre dicha dirección
de los dos vectores siguientes:
• El vector que representa al de los esfuerzos, pero medido desde el punto de máximo alejamiento a la superficie de rotura,
más su distancia hasta el punto de rotura
s – s0 + ag;
• El vector de carga mismo, medido desde
el mismo origen: s - s0.
Es decir, el margen de seguridad se medirá
por el cociente entre los segmentos AC y AB
de la figura.
5
y para dicho punto de rotura se obtendría
la igualdad:
g · (σ + αg) − d = 0
· (σ
αg)
− d = 0determinar
expresióngen
la +
que
podemos
d−g·σ
fácilmente: α =
α=
Nótese que si en la Figura 5 se consideran
puntos arbitrarios, por ejemplo porque el
procedimiento de análisis empleado comparase el estado de esfuerzos con todos los planos que aproximan la superficie, tendremos
que según se aleja el punto B que representa
la proyección de los esfuerzos considerados
del que representa la proyección de los esfuerzos de rotura C, el margen de seguridad
crecerá hasta hacerse infinito cuando B coincida con A, e incluso cambiará de signo
si pasa a estar situado en la proyección más
allá de A, es decir, si el centro de la figug ·más
(σ +
αg) del
− dplano
= 0 de rotura
ra quedase
cerca
considerado que el punto cuya distancia se
comprueba.
d−g·σ
α=
g·g
La distancia entre el estado seguro y el de rotura próximo se puede definir con el vector,
por ser proporcional al gradiente señalado, y
d −más
g · σarriba
g · (σ de
+ αg)
− g · σdefinido
0
0
elγ margen
seguridad
=
=
3 · (σ − σ 0 )
g
·
(σ
−
σ
)
g
0
puede medirse, por tanto con
Tanto en esta expresión como
en las sucesivas, se hace uso
de operaciones vectoriales, de
modo que las sumas y restas son
de vectores, el punto representa
producto escalar, etc...
3
Efectivamente, si se da dicha
coincidencia, s0 será el vector
nulo, de modo que el coeficiente resultante, g = d/g · s, cociente entre proyecciones sobre la
ortogonal al plano, coincide
por Tales con el coeficiente de
seguridad mecánico habitual,
cociente entre los módulos de
los dos vectores colineales que
representan uno, la llegada al
plano de rotura, y otro, el estado
de esfuerzos considerado.
4
36
γ=
g · (σ − σ 0 + αg)
g · (σ − σ 0 )
[1]
Ahora bien, si consideramos el plano tangente como una aproximación de la superficie de rotura en el entorno considerado, la
comprobación tendrá como forma general
para cada uno de tales planos la expresión
g · s - d ≤ 0 expresión en la que si g es unitario representará el versor del plano, y la
comprobación mostrará que la proyección
del vector que representa el estado considerado seguro sobre dicho versor debe ser
menor que la distancia del origen —esfuerzo
o carga nulos— a dicho plano. Nótese que
la ecuación del plano considerado es precisamente la anterior particularizada para el
caso de igualdad: g · s – d = 0. Para este
plano, el punto de rotura más próximo al del
estado analizado se representa con (s + ag)
g·g
d−g·σ
g·g
d − g · σ0
g · (σque:
+ αg) − g · σ 0
Resultará
=
γ=
g · (σ − σ 0 )
g · (σ − σ 0 )
d − ga· σ
g · (σ + αg) − g · σ 0 interior
•γ si
la0 su= a > 0 , el estado es =
· (σgtanto
−· (σ
σ 0seguro
)− σ 0 +
gαg)
· (σgrado
− σ 0 )de
perficie, ygpor
—con
γ=
seguridad a determinar—
g · (σ − σ 0 )
· (σ − σ 0 + αg)
• si a = 0 , el g
γ = estado es de rotura
• si a < 0 , el estado
es
a la su· (σ−
−dexterior
σ=
0)
g · (σ +gαg)
0
perficie de rotura y por tanto imposible de
alcanzar.
α=
d−g·σ
El margen de seguridad
g ·para
g el primero de
los casos anteriores, siguiendo la ecuación
descrita más arriba será:
γ=
d − g · σ0
g · (σ + αg) − g · σ 0
=
[2]
g · (σ − σ 0 )
g · (σ − σ 0 )
De este modo,
podemos
los
αg)
g ·si(σ
− σ 0 +determinar
γ=
gradientes
a la superficie
g · (σ −—los
σ 0 ) planos tangentes a ésta en las regiones de interés— y
las posiciones de tales planos tangentes de
mayor cercanía a los estados a comprobar,
la determinación del grado de seguridad es
extremadamente sencilla, no presenta los
inconvenientes derivados de la mayor o
menor proximidad del punto de carga nula
a la superficie límite, y finalmente es consistente con los modelos al uso en los casos
en que el punto de carga nula y el centro de
la superficie límite coinciden4.
3. EJEMPLOS
Como aplicación rápida del anterior criterio, procedemos al análisis de la resistencia
en compresión excéntrica para secciones
doblemente simétricas. Consideraremos
tanto los casos en que exista resistencia
en tracción —que consideraremos igual a
la de compresión como es el caso de los
metales— o el caso en que ésta sea despreciable. Para referirnos a cada uno de los
Informes de la Construcción, Vol. 62, 518, 33-42, abril-junio 2010. ISSN: 0020-0883. eISSN: 1988-3234. doi: 10.3989/ic.08.045
Un criterio robusto para la medida del margen –coeficiente– de seguridad
A robust approach for measuring the margin –coefficient– of security
casos, los denominaremos respectivamente
metales y fábricas.
6. Vértices para el poliedro de rotura.
Para la simplificación que vamos a proponer supondremos además, como es habitual, que la superficie de fluencia para la
combinación de esfuerzos de colapso por
compresión excéntrica para cualquiera de
los ejes es convexa, por lo que las superficies formadas por poliedros inscritos en
dicha superficie están del lado de la seguridad.
8. Poliedros de rotura.
Para determinar uno de los poliedros posibles, consideramos varias condiciones de
colapso, de acuerdo con los seis criterios
de la Figura 6, en la que pueden considerarse los dos sombreados como estados de
tensión opuestos para los dos casos estudiados: en el caso de haber resistencia en
tracción se tratará de estados de compresión o de tracción, según el sombreado, y
en el caso de no haber resistencia en tracción, se tratará de una región comprimida y la otra sin tensión. Para cada criterio
pueden determinarse las áreas resultantes
y los momentos estáticos de dichas áreas
con relación al centro de gravedad, que
representarán adecuadamente las resistencias axiales, o los momentos resistentes, si
multiplicamos dichas constantes estáticas
por la resistencia unitaria del material empleado.
7. Línea neutra recta.
6
Tendremos, pues, que los valores estáticos representativos de las seis condiciones
de rotura representadas en la figura 6 son,
representados en formato vectorial, los siguientes:
˜
−A 0 0
˜
1
1
Wpl,x 2 ˜Wpl,y
2
ˆ0 Wpl,x 0˜
0 0 Wpl,y
ˆ1
˜
A ˆ12 Wpl,x 12˜ Wpl,y
2
A 0 0
− 12 Aˆ
ˆ
ˆ
ˆ
0
A
0
0
0
˜
A 14 Wpl,x 14 Wpl,y
4 ˆ
˜
1
1
0˜
ˆ 21 A 2 Wpl,x
1
ˆ 3 2 A1 0 2 W1pl,y ˜
A
W
4
ˆ4 pl,x 4˜ Wpl,y
ˆ1
˜
0
ˆ
˜
ˆ
˜
−A por
0 tanto,
0
0 0 0
Estos valores
los
vértices
ˆ 1definen,
˜
ˆ
˜
1
1
− 2 Aˆ de12 rotura
Wpl,x que
Wpl,y
A 1 Wpl,x 14 Wpl,y
4 ˆ M4
de los
NEpoliedros
NE
ME,x 2 ˜ estamos
ME,x conME,y ˜
E,y1
1
n=
= que,ˆm
=
, my ˆ=2 A 2 =
0podemos
Wpl,x ver
0
Wpl,x 0˜.
x =
siderando
NR yAf
MR,x ˜representados
Wpl,x fy
W
y
1 MR,y
1 pl,y fy
0
0
W
A
0
Wpl,y ˜
pl,y
en la Figura
escala corresponde
2
ˆ 18, cuya
˜
ˆa 3los2 1
1
1
1
ˆ
˜
ˆ adimensionales
˜ 2 A de
W
W
A
W
pl,x
pl,y
pl,x
comprobación
siguien2
4
4
ˆ2
˜
ˆ4
˜ Wpl,y
Por ejemplo, si −A
de acuerdo
0 0 con ˜los crite0 0 0
ˆ 1
ˆ
˜
A por
0 referencia
0
A 0 0
tes,
que
obtenemos
a
las
re1
1
1
1
1
rios de la−figura
área de4 Ala 4 Wpl,x 4 Wpl,y
A llamamos
Wpl,x 2A˜Wal
pl,y
2 ˆ
2
ˆ
˜
de secciones de las que
1
sección, y Ex, E0y a W
los
momentos
estáticos12 A sistencias
0
Wpl,x plásticas
0˜
pl,x
2
˜
ˆ1
ˆ
hemos
1 llamado metálicas:
de media sección
respecto
del
centro
de
0 0 Wpl,y
y ; Mx,R = Wpl,x fy ; My,R = Wpl,y fy
pl,y
ˆ
˜
ˆ 2 A1 0NR2=WAf
˜
gravedad, 1tendremos
de Wpl,x 1 Wpl,y
A ˆ12 Wpl,xque 12˜para
Wpl,yel caso34 A
4
2
ˆ4
˜
NE
NE
ME,x
ME,x
ME,y
ME,y
materiales metálicos
y en la no- An =0 0 =
, mx =
=
, my =
=
.
A 0plásticos,
0
NR
Afy
MR,x
Wpl,x fy
MR,y
Wpl,y fy
menclatura habitual en los Eurocódigos,
las constantes estáticas relevantes serían
el área A, y los módulos plásticos Wpl,x =
Se están representando sólo las regiones po2Ex N
y EWpl,y N
= E2Ey, y tendríamos
como
límites ME,ysitivasMen
ME,x
M
E,x
E,ylos valores de los momentos; las
nde
= resistencia
=
, mx =
=
, my =
=
.
máximos
obtenerse por simetría.
NR
Afy para los
MR,x
Wpl,xesfuerzos
fy
MR,ynegativas
Wpl,y fpodrían
y
N
R = Afy ; Mx,R = Wpl,x fy ; My,R = Wpl,y fy
positivos en cada uno de los los tres ejes
independientes necesarios para representar
Vemos que en dicha figura, los centros de
los estados de flexocompresión o flexotraccada poliedro corresponden a las coordenación:
das s0,m = (0 0 0); s0,f = (0, 5 0 0). Podemos,
pues, determinar las comprobaciones apliNR = Afy ; Mx,R = Wpl,x fy ; My,R = Wpl,y fy
Hay que señalar que en la figura hay dos
estados para los que la línea de paso de un
estado de tensiones al opuesto es quebrada. Se trata de una simplificación del lado
de la seguridad y por lo tanto admisible
dado que, como puede verse en la Figura 7,
establecer una línea neutra recta que separe las dos regiones manteniendo los valores
de las áreas sombreadas supone siempre el
alejamiento del centro de gravedad de la
región respecto de la posición que ocupa
con la forma quebrada lo que incrementa
obviamente los correspondientes momentos estáticos.
7
8
Informes de la Construcción, Vol. 62, 518, 33-42, abril-junio 2010. ISSN: 0020-0883. eISSN: 1988-3234. doi: 10.3989/ic.08.045
37
J. Cervera
cando los criterios definidos en el apartado
anterior.
γf,i =
d − g · σ 0,f
d − 0, 5ag
=
g · (σ − σ 0,f )
g · σ − 0, 5ag
Consideremos el caso de los metales. Ten-
γf,i =
d − g · σ 0,f dremos
d −las
0, 5a
g
d − g ·de
σ 0,f
d − 0,donde
5ag ag es el coeficiente del primer tércomprobaciones
la tabla
=
γf,i =
= sig · (σ − σ 0,f ) guiente,
g·σ−
0, 5a
g deducir
g · (σ −
)
g · σ −mino
0, 5ade
g la ecuación del plano g · s - d =
fáciles
de
de σla0,fexpresión
d
en=
la que g = (ag bg cg)(*), aunque resulta
γ0,m,i
que resulta para la condición de s0,m = (0
g
σ
preferible ·representar
las comprobaciones
0 0):
γm,i
d
=
g·σ
en la forma(**)
γm,i
d
=
g·σ
Hay que hacer
notar que 3
en las comproba2
ciones aplicadas
a0las secciones
que hemos
1
0
4 0 fábricas,
γm,1 = n
1
0 5
n + mx = 1
denominado
estamos
empleando
0, 5 0,
5 las
0, 5resistencias
como referencia
para
las de
2
3
2
3
2
3
0
los metales, 1lo que0 no supone
diferencia en
1
0
0
1
0
0
4 límite
γm,2 = n
0
0
1 51
n + my = 1
1
el
caso
del
para
esfuerzos
4 0
5
=
1
0 5
n + mx = 1 4 0 γm,1
γm,1 = n+mx axiales NR,
1
0 x
n + mx = 1
n+m
0,
5
0,
5
0,
5
pero
sí
para
los
máximos
flectores
admisi2
3
20, 5 0, 5 0, 53
20, 5 0, 5 0, 53
0, 5 si 0,hay
5 resistencia en
bles, que ∓0,
es 5doble
1
0
0
1
0
0
4 0
γm,3 = m
1 estamos
0 51 determinando
mx + my = 1
1
4d 0− g ·0σ 1 5
myg = 1 4 0 γm,2
= n+m
0 = n+m
1 5y
ntracción.
+ my = 1Es decir,γm,2
d −n0,+5a
0,f
y
0
0
1
γf,i = 0, 5 0, 5 0, 5 =
mx = ME,x2/MR,x empleando 3para el valor de
2g · (σ − σ 0,f ) 3 g · σ − 0, 5ag 2 0, 5 0, 5 0, 5 3
−0, 5 a0, partir
5 0, 5del módulo plásMR,x el obtenido
∓0, 5 0, 5 0, 5
∓0, 5 0, 5 0, 5
4
γm,4 = −n
0
1
0 51 Hemos
−n + m
1
x = 1
4 0
5y
considerando
tracciones.
he1
0 5
mx + my = 14 0 γm,3 1= mx0+m
γm,3
= mx +m
mtico,
x +m
y = 1
y
−1
0
0
3
0
1 3
cho eso 2
para facilitar la comparación
entre
0
1 3
2 0
2 0
−0, 5 0, 5 0, 5
−0, 5 0, 5 0, 5
ambos casos,
pero sería razonable
que las
−0, 5 0, 5 0, 5
d
4
5
γm,5 = −n
0
0
1 1
−n + my = 1
1
1
0 5
−n + mx = 14 0 γm,41= −n+m
γm,i =4 0
máximas
determinen
a par1
γm,4 se
= −n+m
0 5x
−n
+ mx =resistencias
x
−1
0
0
g−1
·σ 0
0 3
0
0 3
tir de las cualidades propias del problema
2
2 −1
−0, 5 0, 5 0, 5
−0, 5 0, 5 0, 5
considerado. Si estamos hablando de fá1
1
4 0
0
1 5
−n + my = 14 0 γm,50= −n+m
= 1considerar
γm,5 el
= recurso
1 5y
−n
+ mysin
bricas
−n+my a las trac−1
0
0
−1
0
0
ciones podemos
rehacer
el razonamiento
2
3
2
3
1
0
0
1 0 0 ahora como vértices
completo empleando
1
4 0
γm,1 = n+m
1
0 5
n + mx = 1
40 los1 puntos:
del poliedro
05
n + mx + my = 1
γm,0 = n+mx1 +
x
0,
5
0,
5
0,
5
Nótese
que las comprobaciones numeradas
0 0 1
2
3
2 1
03 0
2 realidad 3
1 y 4 y las 2 y 5, son en
las mismas
1f
(0 0 0)
1 0 γm,2
0 = 1
41 0 0 00
5 el signo
= 1esfuerzos
1
n + en
my los
salvo
axiales.
1 n+mLas
2f
(0,25
0,5 =
0,5) 1
y
40 1 05
4
5
n
+
m
+
m
=
1
γ
=
y
m,0
0 1 n+m
0 x +mny+ mx + my = 1
γm,0
53 x
precisas son las
1, 2 y 3 si
200, 50 0,15 0,comprobaciones
3f
(0,5 1 0) n+mx +my
0
0
1
∓0, 5 0, 5 0,
5
consideramos
sólo las comprobaciones1que
4f
(0,5 0 1)
4 0
γm,3 =o m
1
0 5
mx +a m
y = 1 positivos,
corresponden
valores
absolux +my
5f
(0,75 0,5 0,5)
0
1 3en n, mx, my, es decir, empleando sólo
2 0
tos,
6f
(1 0 0)
−0, 5 0, 5 0, 5
el triedro
positivo del poliedro de rotura.
1
4 0
γm,4 = −n+m
1
0 5
−n + mx = 1
x
y con ello determinar las comprobaciones
0
0 3
2 −1
Véase
que
si
hubiésemos
ignorado
los
vérresultantes. Es fácil ver, sin embargo, que en
−0, 5 0, 5 0, 5
tices
y 5m del
poliedro,
1 de
el caso que estamos analizando de seccio4 0
γm,5
= −n+m
0
1 5 numerados
−n + m2m
y = 1
y
modo
a
aproximar
la
superficie
en
el
triedro
nes doblemente simétricas la máxima re−1
0
0
positivo sólo con un plano, la comprobación
sistencia axial es idéntica, mientras que los
que resultaría ahora sería:
máximos flectores admitidos son mitad de
los de las secciones metálicas, por lo que
si referimos los correspondientes adimen2
3
1 0 0
sionales a dicho valor mitad, las compro40 1 05
n + mx + my = 1
γm,0 = n+mx1 +my
baciones que ya hemos obtenido se trans0 0 1
formarán en(***). Como ya se ha dicho, el
margen —o coeficiente— de seguridad de
Dicha comprobación es la habitual en los
la sección para los esfuerzos considerados
códigos, y como puede verse es innecesariasería el positivo de menor valor de entre
mente conservadora, pudiendo ser sustituída
los obtenidos, recordando que los valores
con generalidad por el conjunto de las tres
negativos tienen como significado el hecho
primeras de la tabla precedente que, como
de que el plano que se emplea para la combien se ve, sólo contrastan la interacción del
probación estaría más lejos del punto que
esfuerzo axial o los momentos flectores para
representa los esfuerzos que se compruecada uno de los dos planos de flexión, conban que el centro del poliedro.
siderados de dos en dos.
Podemos comparar ahora el resultado que
Si consideramos ahora el caso de las seccionuestro criterio de comprobación aporta
nes de fábrica, sin resistencia a la tracción,
para determinar la seguridad en la altura de
para la condición de s0,f = (0, 5 0 0 ) tendreun prisma rígido apoyado en su base cuamos las comprobaciones:
drada, comparando con los criterios habi-
38
Informes de la Construcción, Vol. 62, 518, 33-42, abril-junio 2010. ISSN: 0020-0883. eISSN: 1988-3234. doi: 10.3989/ic.08.045
Un criterio robusto para la medida del margen –coeficiente– de seguridad
A robust approach for measuring the margin –coefficient– of security
(*)
2
3
1
0
0
4 0, 5
0, 5
0 5
n + mx = 1
γf,1 = n+m0,5
x −0,5
0, 75 0, 25 0, 253
22
3
11
00
00
0,50,5
0,
5
0
55
γf,2== n+m
44
0, 5
0, 5
00, 5
nn
++
mm
==1 1
γf,1
x y
y −0,5
n+mx −0,5
2 0, 75 0, 25 0, 25
3
220,175 0,025 0,0253 3
∓0,
25
4 0,
15 75 0,00,
5 25 00,5
n + mx = 1
γf,1 = n+m0,5
−0,5
x0,5
0,5
20,0,
5 0,025
0, 5 0,
053 5
m
+mm
0, 5
= m
44
x
y==
5
0,
5
n
+
1
γf,2γf,3
= n+m
+m
y
0,
75
25
1
0
03
yx−0,5y
2 0,
5 0,0250 0,025
0, 5
53
0,5
0,
75
1
2
4
0, 5
0 3
n + mx = 1
γf,1 = n+mx −0,5
2 0, 5
0,575
25 0,00,25
25 0,
25
4∓0,
5
0,0,525
25
0,
n + my = 1
γf,2 = n+m0,5
0,
75
0,
25
0,
−0,5
y0,5
4
5
0,55 0, 25
+ym=x 0,
=50
γγf,4
= 0,5
4 20,
5
0, 150 0,0,25
00 3
mx−n
+m
f,3 = −n+m
mx +mxy+0,5
0
0
2 75
3
0 0,025
0 0,
05 53
0,0,575
0,25
42
5
0
0,
53
n + my = 1
γf,2 = n+m0,5
2∓0,
y −0,5
0,
25 0,0,
0,
25 0,0,
255
4 0,
25
25
25
0,
5
5
0
m
+
m
=
0,
5
γf,3 = mx0,5
x
y
0, 75 0, 25 0, 25 5
+m
0,5y
0,5
2
3
0
0
0,
5
−n
+
m
=
0
γ
=
44
5
y
f,5
00, 525
−n + mx = 0
γf,4 = −n+m
−n+m+0,5
+0,5
0,0575 0,0,0525 0,
x y
2∓0,
3
0
0
02505 0,025
4
0, 5 0,02503 5
mx + my = 0, 5
γf,3 = mx0,5
20,0,
+my
0,5
40,0,
025 0,
0,25
50 0,025
−n + mx = 0
γf,4 = −n+m
0, 5
53
x +0,5
0,5
1
1
2 51
4
5
+ my = 0
γf,5 =
= −n+my +0,5
γf,1 =2 2n+2m
γ3f,2 = −n
γf,3
0,0 25 x
0,0−1
25 0,
0,0525
2n+2my −1
2mx +2my
0,5
0255 0,025
0,025
5
(**)
0 1 0,0,
0γf,5
−n +1mx = 0
γf,4 = −n+m
γf,4 = 44
= −2n+2m
0,5 x +0,5
−2n+2m
+1
x +1 0, 5 5
00
0
−n + myy=
0
γf,5 = −n+m
0
0
y +0,5
2 1
3
1
1
γf,1 = 2n+2m
γf,3 = 2mx +2m
0,0 25 −1
0,0 25 0,0γ25
f,2 = 2n+2my −1
x
y
0,5
4 01 1 0
1
2 = −n1+1my = 3
0, 5γ5
0
γf,5 =
= −n+m
+0,5
γf,1
γ
y
γf,4
==
γ
=
f,2
f,3
f,5 1 −2n+2m
01 y+1
0
2
3
1 +my
2n+m
2n+m
mx
−1
−1
0 1 xx+1
0
0 0 =
γf,1 = −2n+2m
0,5
0 0, 5 y1y−10 5 γf,3 =
1 −1 1 γf,2
4 0, 5 2n+2m
2m
x
x
n
+
m
=1y
γ0,5
x +2m
f,1 = n+mx −0,5
γf,4 =2n+2m
γ
=
f,5
4
5
1
1
−2n+m
−2n+m
+1
+1
0,
5
0,
5
0
n
+
m
=
1
γ
=
x
y 25
x
f,1
n+mx −0,5
γf,4 = −2n+2m
γf,52=
0, 75−2n+2m
0, 251 0,
11 x +10, 75 γ0,f,2
1 y +1 3 γf,3 =
11
25 =
0,2n+2m
253
= 2n+2m
=
f,1 =
γγf,1
γ
γ
=
(***)
1
0
0
2
f,2
f,3
2m
−1
−1
+2m
2n+mxx−1
2n+myy−1
mxx+my y
0,5
1 M4
0E,x
N
N11E
0,
5 0M0E,x
=1
11 0, 5 5 ME,yn + mM
y E,y
f,2 = n+my −0,5
=E −2n+2m
γ
=
f,4
f,5
= =
=
,
m
=
=
,
m
=
=
. = 3 γ0,5
γnγf,4
γ
=
4
5
x
y
−2n+2m
+1
+1
f,5
y+1n + m2
1 xx+10, 5
1
1
0
0,
5
=
1
γ
y
f,2
−2n+m
−2n+m
y
n+m
−0,5
0,=
75 E
0,x25
Afy −1
fy 0, 25 3 γM
y
γf,1N=R 2n+m
γMf,2
R,y
y fy 0
f,3
1= mE
0+m
2R,x
x
x
y
0,2n+m
250,325y −1
∓0, 75
0, 25
2 0, 75 0, 25
4 0, 5
5
1
1
0,
5
0
n + mx = 1
γf,4N=
γf,5
=5 −2n+m
∓0, 75M
0, 25
0, 250, 51 y +10 5M m +M
4
1 0, 5
−2n+m
3 N
0,
M
h E 1 x +1
=
γf,3 = mx0,5
3
x= m
y
E=a
E,x
E,x
E,y
E,y
2
+my
γ
γ
=
γ
0,
75
0,
25
0,
25
ρ
0,5
ρa
f,1
f,2
f,3
4.x 0,=5
h 5 mx
h 2n+m
ρh 5 , ym
2F ρh
ρa
F+
h m2
2
n 1=≤ γ1 = = 2n+m
, xm
=
−1
−1
3mx +my
0, 50,=
m
γ. f,3
y x=
y==4n
y 8=F0,
5=E0x f;y0 m
0,
5a3
=R,y
=
4y0f+m
nM
=R,x
x =
NR F hAf=
E
3 M
1
0
y1 2F
y
2
3
3
2
1
a f
a0 f= 0,f5
ρa f
γ1
γf,4
γE,x
f,5
0, 25 M
0,
258 fME,y
2 0, 5 M
325 y0,+1
4 0, 5 ME,y
NE= −2n+m
NE x +1
−2n+m
E,x
0
0, 5 5
n+m
=1
0,5y
25 0,425 =
0, 250, 5 , m
ndonde
= ahora
=
,
m
=
=
.
5
x0,=
y
0
0
−n
+
m
=
0
x
f,4 = −n+mx +0,5
0,=750 E
0,y25
0,=25 3γ0,5
2
NRa3 ρ h2Af
E0 x f5y
Mm
f
R,x
R,y
y
1 yρa3 4 0 1Mρa
2
0,
5
−n
+
γ
F
h
h
ρh
2F
ρh
4n
F
h
x
f,4
−n+mx +0,5
γ
=
. 0= M; 0mx = 0 3 =M
1 ≤1 γ≤1 N
=2 =
=
.
8∓0,
= 4M
=0, 25
n = 4E,x
75
0, 25
N
E F hn +
E2F
E,x
E,y
22
3f
m
a3
n(1
x
0=+M
0)f = f0
a3 f = ρaE,y
γ1 5
γa
f
n=
=
,
m
,
m
=
.
0,
25
0,
25
1 0, 25
2
3
x
y
4
8
0, 5 E0,
5y
0
mx + m
= 0, 5
225
NRa3 ρ h2 Afρa
0,5y
0, 25 M0,R,x
0,E
25x0fy 0,F5h5 MR,y
y 3
yf
Fh
2F
−n
+4 m
= 0=0,4n
γ0,5
yρh
f,5 = −n+my +0,5
1 ≤ γ1 =
=
. 4 n = ρa4h 0= ρh ; 5
0,
5
0
5
=
8
m
=
=
x
3
01
3=
3γf,5 = γ 3
F h 1 2F
a.20f 0 0,f 5 0
f250 0,ρa
−n+m
0a−n
1
y +0,5
f + m2ay0,
1 ≤ γ2 = 3 h
=
25f 0, 25
8
02 h
0ρh
an ρ+2 mx ρa3 n(1 0+ γ41 )ρa
2F ρh con
4n
F hel caso
4 Fh
5resistencia
tad en
de secciones
tuales.
Sea el prisma
−n + mx = 0
1 ≤ γ1 =
=
.de base=cuadrada
= de; mx = a3 = 8 30 =1 40, 5 3 =0
1
F h1
2F peso1nespecífico
a 0f es la0ρa
a. 2 f 1r. fSi
f 0γ
γen
en tracción
—y
habitual
1 comprof
γ
=
=
1lado
≤ γa2 y=altura h con
= γf,11 =
f,2
f,3
8
1 2 2n+2my −1
4
3 1
2n+2mx
2mx +2my
−1 =
n+
mx =efecto
n(1
+
)
γcomo
γ
γ
=
baciones
plásticas
en
metales
tal
como
las
f,1
f,2
f,3
consideramos
de
perturbación
γ1x −1
0, 25 1 0, 25 0, 2m
25 x +2my
2n+2m
2n+2my −1
1
γf,5 1= 4ejemplo,
f,411=horizontal
1 unaγfuerza
el0yEurocódigo
−2n+2m
−2n+2m
+1 0, 5 5 3— pero
para
equilibrio
F,
x +1=define, por
0
−n + my = 0
γf,4
==−2n+2m
γ
1 ≤ γsu2 =
.
f,5
y +1su forma de empleo cuando
no−2n+2m
es evidente
mx deln(1
situada en nlo+alto
prisma,
tendremos
+ γ41x)+1
0
0
0
los momentos se resisten sólo mediante las
como resultantes de esfuerzos los tres valo1
1
1
γf,11 = 2n+m
γf,21comprimidas
= 2n+m
γf,3
regiones
excéntricamente.
res (a2hr Fh 0).
1 = mx1+my
1
x −1
y −1
γf,1 = 2n+mx −1 1 γf,2 =γf,1
γf,3 = γmf,2
= y2n+2m
=
−1
1−1
x +my2n+2my −1
x
γf,4 1= −2n+mx +1 γ2n+m
f,5 1= −2n+m
1 todo,
1
+1
y
Usaremos,
pese
a
el
área
y
el
momenConsideremos
ahora
criterios de se= −2n+2m
γf,5 = −2n+2m
γf,4
= varios
γf,5 =γf,4
−2n+mx +1
−2n+m
x +1
y +1
y +1
guridad. El primero, clásico para el análisis
NE comparaNE
de la estabilidad frente al vuelco,
, E,x
mx
Nestabilizante
M
E n =NE y=
rá los momentos
desestabiN
Af
n=
=
R, mx =y
NRel vuelco
Afy en torno aMlaR,x
lizante suponiendo
arista exterior.
3 h
3
1 ≤ γ1 =
to estático de media sección comprimida
como
referencias
para los mayores
ME,x
ME,x
ME,y valores
ME,y
=
, E,y
my =alcanzarse,
M
ME,y = de 1 .
E,x =
1 M
de
resistencia
que
puedan
γ
=
γ
=
M
E
f
M
Ey fy
= f,1
my x=yx −1 = f,2
R,x , 2n+m
R,y .
modo
Exque:
fy
MR,y
Ey fy 2n+my −1
γf,4 =
1
−2n+mx +1
γf,5 =
1
−2n+my +1
γf,1 =
0,5
n+mx −0,5
γf,2 =
0,5
n+my −0,5
γf,3 =
0,5
mx +my
γf,4 =
0,5
−n+mx +0,5
γf,5 =
0,5
−n+my +0,5
γf,3 =
γf,3 =
1
2mx +2my
1
mx +my
a ρ2
ρa
Fh
2F ρh
4n
Fh
. 2 h n =ρhρa h = ρh
a13 ρ≤h2 γ1 =
8 ρh
= 44n 3 =
ρa3F h = 2Fρa
F ;h mx =F ah3 = 2F
2f
3f
=
.
a
f
a
ρa
f
γ1
= 8 3 8 f=
; mx = N
4 3 =M
n= 2 = N
Fh
2F
a3E
a f ME,x
f E
ρa f
γE,x
a f
1
f
2
ME,y
ME,y
= 8 , mx =
=
, my =
=
.
N
Af
M
E
f
M
Ey fy
R
y
R,x
x
y
R,y
1
expresión
en la que hemos usado el valor
.
n=
1
El segundo corresponderá
1 ≤1 γ2 a= la compro1 =
bación de 1resistencia.
+ γ41 ) para g1 en la expresión preceden≤ γ2 = Si suponemos
=n + mxque
.n(1 obtenido
n
+
m
n(1tensión
+ γ41 )
x una
te. Si establecemos
la base es capaz de soportar
a3 ρ h
ρa3ahora la forma
Fh
ρh
2F ρh
4n
ρa2 h de inteFh
1racción
≤ γ1 =lineal2 de
= forma
. ingenua
=
; mx = a3 = 8 3 = 4 3 =
n = tendríamos
máxima f, podemos usar ahora la comproFh
2F
a f
f
ρa f
γ1
a2 f
f
8
como criterio de seguridad:
bación clásica que combina linealmente las
pérdidas de resistencia derivadas de tener
1
1
1 ≤ γ2 =
=
.
que soportar simultáneamente axil y mon + mx
n(1 + γ41 )
mento. Dicha expresión se usa sin dificulInformes de la Construcción, Vol. 62, 518, 33-42, abril-junio 2010. ISSN: 0020-0883. eISSN: 1988-3234. doi: 10.3989/ic.08.045
39
J. Cervera
mento estabilizante que cabe obtener para
una resistencia dada en el terreno de apoyo
sería el de media sección del apoyo completamente comprimida, y, por tanto, con
brazo mitad respecto al considerado en
la comprobación clásica. Para otras áreas
comprimidas, tanto si son mayores como si
son menores, el momento estabilizante re«
„
«
sultará siempre menor que dicho máximo.
1
1
1,
1
≤
γ
3 = mı́n1
1 ≤ γ3 = mı́n
, x − 1 −2n + mx +Al
1 aproximar el coeficiente de seguridad
2n + mx2n
−+
1m
−2n + mx + 1
mediante una sola expresión para todos los
casos resulta un factor de 2 en menor efio lo que es lo mismo,
cacia para el caso límite en que no hay casi
„
«
„
carga,
ni por lo tanto momento de vuel1 “ «1
”
1
1
1
≤
γ
≤
3
1
1
“
”
1
≤
γ
≤
3
1
≤
γ
=
mı́n
,
4
1
3
1 ≤ γ3 = mı́n
,
co. Una visión en detalle de la superficie
21+
1 γ −2n
2n + mx − 1 −2n
n + mx − 1 −2n + mx + 1
n 2++mγn4x1 +−
n 1
de fluencia en las proximidades del punto
1
1“
”
1
≤
γ
≤
de carga nula comparada con la superficie
3
”4
1 ≤ γ3 ≤ “
1
1 γ + n
aproximada por los planos del poliedro gen −2 +n γ41−2
++
1
n
1
1
nerado a partir de los casos de rotura con”
1 ≤ γ3 ≤ “
”
1 ≤ γ3 ≤ “
4
1
4
1
siderados —los situados entre la separación
−
n
2
+
finalmente
comparar
las
prescrip−
n 2 + γPodemos
γ1
n
n
1
por tracción y el vuelco con hundimiento
γ
≥
1
1
ciones
de
dichos
criterios
de
seguridad.
Los
1
1 γ1 ≥ 1
de media sección, ver figura 9— aclara la
“ las versiones
”
1 ≤ γ3 ≤ por
” establecidos
requisitos
1 ≤ γ3 ≤ “
1
4
1
4
11
n—comprobación
≤
n
−2
+
+
diferencia entre ambos valores: la forma
n −2 +n
+
4
clásicas
de
vuelco,
y
re≤
γ1
n
γ1
n 4 1+
γ1
1 + γcombinada
exacta corresponde a la llegada a dicho
sistencia
a hundimiento y vuel1
punto de la rama de una parábola, que pasa
co— son:
por los puntos que representan ambos caγ
≥
1
1
γ1 ≥ 1
sos, frente a una recta para la versión pro1 1
1
2 1
1
n 1≤1
1
1 4 1− 1 ; 1 2≥puesta
n≤
aquí. La pendiente
de la rama de la
n
≤
;
≥
2
+
4 4
4
4
1
2
n≤
1≥+2 γ+1n − ;γ1 ≥n1 +n ;1n+≤γ1 ; n ≤
1 + γ1
1
+
4 2+
1 ;γ −
2
γ1es doble a la pendienγ1
n n
γ1parábola
en γel1 origen
2 + γ1 − n 1n n
1+
1 1
1 aporta
4
1te4 de la 4recta. La expresión clásica frente
El tercer criterio
1las
n ≤1 aquí; 4propuesto
≥4−2
1 ;
n≤
++ ;γ12 +
≥ na ; vuelco
;2 γ≥1 ≥
2; γ1 ≥ 2
usar como aproximación
γ1supone
4−2 +
1 γ +≥n−2n+
condiciones
siguientes:
γ1
n
γ1
−2 + γ1 + n 1n
a dicha rama parabólica la recta tangente
1 2
1
1 1
2
1
4
1
1
1 1
1 4
en1el+ origen,
lo que 2está en contra
; n≤
≥2+
n≤
;
− n ;≤ ≥ 14+ 1;; n ≤≥ 2 + 2 − a ;ella ≥
n seguridad.
n
γLa
1 + γaquí
1 expresión
γ1
n n2 + γ1 −γ1n n 1 + γγ1 de
2 + γ41 − n1 n
propuesta
1
1
usa,
secante, segura, aun14
1
4 en1vez, la recta
4
1
1
1
4
; 2≥
; γ1 ≥ 2
n≤
;
≥ −2 + n+≤ ; 2 ≥ 4 ; γ11; ≥ 2≥ −2 +que +
para los casos de
γ1 más
n conservadora
γ1
γ1
n−2 + γγ1 1+ n n
−2 + γ41 + n1 n
casi ni carga ni vuelco.
Como se ve, el criterio que acabamos de esLa primera de las dos comprobaciones obtablecer aporta por sí solo dos expresiones
tenidas con el criterio aquí propuesto estasemejantes a las ya obtenidas mediante los
blece un límite a la carga que puede suponer
dos criterios anteriores. Se trata de expresioel peso del bloque en relación con la carga
nes cuya confiabilidad es mayor.
centrada que puede soportar el apoyo. La
expresión para ese límite es de mismo tipo
Si empezamos por la segunda de ellas, la
al obtenido mediante un razonamiento cládiferencia contra la clásica expresión de essico y un diagrama de interacción lineal, y
tabilidad contra el vuelco deriva de que, al
permite valores superiores a dicha relación,
no poderse considerar el apoyo en la arista
si bien ahora, dado que no hay confusión
exterior como si fuese infinitamente rígido y
posible en cómo establecer las resistencias
resistente, el grado de seguridad que aporta
máximas en carga y en carga excéntrica, la
la expresión clásica es diferente, en contra
expresión resulta completamente satisfacde la seguridad. La expresión alternativa que
toria. El error en la expresión inicial deriva
se presenta aquí refleja que el mayor moprecisamente de haber considerado normal
y momento máximos como independientes
al construir la recta de interacción, cuando
en realidad el momento máximo está ligado a un normal mitad del máximo.
En contraste empleamos ahora el criterio
que acabamos de establecer, para el apoyo
sin resistencia en tracción, y con tensiones
de compresión limitadas al valor f, tendremos como tercer criterio de resistencia el
siguiente, considerando sólo los dos planos
de interacción entre el esfuerzo axial y el
momento en una dirección:
„
4. CONCLUSIONES
9. Dos criterios de vuelco.
40
9
Se ha propuesto un criterio de seguridad
que considera condiciones de rotura no
necesariamente isótropas, y no necesariamente centradas respecto del punto de carga o esfuerzo nulo.
Informes de la Construcción, Vol. 62, 518, 33-42, abril-junio 2010. ISSN: 0020-0883. eISSN: 1988-3234. doi: 10.3989/ic.08.045
Un criterio robusto para la medida del margen –coeficiente– de seguridad
A robust approach for measuring the margin –coefficient– of security
Se ha comprobado que dicho criterio resulta consistente con los habituales en los casos en que las condiciones de colapso son
simétricas respecto de la situación de carga
o esfuerzo nulo.
Se ha comprobado que dicho criterio puede aplicarse con eficacia y gran facilidad
tanto al análisis de la resistencia de secciones de materiales perfectamente plásticos y
con simetría en el comportamiento en tracciones y compresiones, como al análisis de
la resistencia de secciones de materiales sin
resistencia a la tracción.
En el caso de materiales plásticos y simétricos se ha comprobado que la aplicación
de dicho criterio —que resulta en este caso
idéntico al habitual— a secciones doblemente simétricas demuestra que en la comprobación de estados de flexocompresión
esviada basta comprobar la resistencia para
la interacción separada del esfuerzo axial
con el momento sea en una o en otra de las
direcciones, y la interacción de ambos momentos conjuntamente pero sin interacción
del esfuerzo axial, es decir, considerando
sólo todas las interacciones entre dichos
esfuerzos tomados de dos en dos.
Se ha comprobado, finalmente, que dicho
criterio permite unificar en un solo modelo criterios de comprobación considerados hasta ahora independientes, como es
el caso de las condiciones de seguridad al
vuelco de un prisma apoyado en una base
de resistencia dada.
ΣANEJO
= Ω L(σ)dΩ
5. 1: BREVES CONSIDERACIONES
RTÉCNICAS
R
aT · L(b)dΩ = Ω LT (a) · bdΩ
Ω
La unificación entre los criterios históricaR
mente
de estabilidad y de reF (Σ) diferenciados
= Ω A(f (σ))dΩ
sistencia puede
interpretarse
con facilidad
R
si σ(Σ)
obtenemos
las comprobaciones de esta= Ω L(σ)dΩ
bilidad como límite de series de comprobaR Tde resistencia
ciones
ε̇ · σdΩ = Ė T ·en
Σ las que la resistencia Ω
a tracción de las fábricas tiende a cero.
R
∂F
Puede asimismo
= ΛE justificarse el empleo de
una ∂Σ
función F(S) para expresar la condición
deRrotura
en casos en que S represenσx (z)dA
N =
te valoresA agregados representativos de un
R
comportamiento
de sección —o pieza o
M = A zσx (z)dA
estructura—. Para ello bastará
» –
» –
N
1
•σ
que
definida
(z); Σ =empleado
; L tenga
=
;
= el
σxmaterial
M
x
una función de plastificación f(s) válida
para las tensiones de punto s —cuyas co» –
» –
rrespondientes
deformaciones ˆse denotan
˜ �
�
E e—
= función εpara
= �la+que
xc =
x
con
sea 1correcta
c
c la
condición de ortogonalidad en la situación
límite:
∂f
= λε
∂σ
• que la caracterización del equilibrio para
el comportamiento agregado pueda hacerse
a través de parámetros de esfuerzo —o incluso de carga— S determinables a partir
de los s mediante expresiones lineales del
R
tipo Σ = Ω L(σ)dΩ, siendo L (·) un operador
lineal,R tal vez diferencial,
R sobre s.
aT · L(b)dΩ = Ω LT (a) · bdΩ
Ω
• que la caracterización cinemática del
R agregado se haga mediante
comportamiento
F (Σ) = Ω A(f
(σ))dΩ
parámetros cinemáticos E tales que las deR
formaciones
σ(Σ) = e Ωpuedan
L(σ)dΩdeducirse de ellos a
través de Rla expresión s = LT (E) donde LT (·)
= T Ω L(σ)dΩ
Roperador
es el Σ
adjunto de L(·), es decir:
ε̇ · σdΩ = Ė T · Σ
Ω
R
R
R
T
a · L(b)dΩ = Ω LT (a) · bdΩ
Σ = ΩΩL(σ)dΩ
R T ∂F = RΛE R
aF (Σ)
·∂Σ
L(b)dΩ
=
LT (a)pueda
· bdΩ construir• Ωque
la =
función
F(S)
A(fΩ(σ))dΩ
R
Ω
R
Σ =expresión
L(σ)dΩ del tipo:
se N
mediante
alguna
Ω
=R A σRx (z)dA
L(σ)dΩ
A constante
F (Σ) σ(Σ)
= Ω=
A(f (σ))dΩ
R , siendo
R
T
R Ω
aT debe
· L(b)dΩ
= ΩL
en el M
dominio,
para
lo Ωque
definirse
al- (a) · bdΩ
=
zσ
(z)dA
R
x
R T A
σ(Σ)forma
= ε̇ Ω ·L(σ)dΩ
guna
para
(s) —lo que
σdΩ la
= relación
Ė T · Σ S
Ω
R
» de
– pseudoinversa,
–
equivaldría a algún Ftipo
(Σ)
=
A(f»(σ))dΩ
Ω
R T
1
T
R Nla inversa
peroε̇σ
no·=
necesariamente
matemá(z);
Σ
=
;
L
=
;
σ
σdΩ
=
Ė
·
Σ
x
R
∂F
Ω
ML(σ)dΩ
x , ya
Ω
= ΛE Σ =σ(Σ)
tica, de la relación:
= Ω L(σ)dΩ
∂Σ
R
señalada antes— R T
∂F
a · L(b)dΩ = Ω LT»(a)
»R –
– · bdΩ
ΩR
T
T ˜
==ΛE
ˆ
σ
(z)dA
N
x
ε̇
·
σdΩ
=
Ė
·Σ�
�
R Ω
∂Σ
E = Ay Σtercera
εΩ L(σ)dΩ
=condiciones
� +R xc = 1aseguran
x
=
La segunda
cR
c
R
(Σ) = Ω A(f (σ))dΩ
= A zσ
que
cambio
representación
N =elM
RdexF(z)dA
R de TcualesRA σx (z)dA
∂F
T
· L(b)dΩ
=
L (a) · bdΩ
quiera
y cinemáticas
Σ = Rcondiciones
L(σ)dΩ
R= ΛE
R Ω a estáticas
Ω
Ω R

∂Σ
»
–
» –
σ(Σ)
=
L(σ)dΩ
Σ
=
L(σ)dΩ
R
s,MRe =aΣ sus
transformadas
S,
E
zσ
(z)dA
Ω se producen
Ω
=
L(σ)dΩ
∂f
A Ωx
N
1
R
R=
Rλε;los
Σ = ΣΩ =
L(σ)dΩ
T
Ten
(z);
L
=
; seσ
=
σ
a
·
L(b)dΩ
=
respetando
la
invariancia
trabajos
x
R
L
(a)
·
bdΩ
R
F
A(f
(σ))dΩ
σ
(z)dA
N
=
Ω R
x
T (Σ)R =
∂σ
Ω
R
M
x
T
Ω
A
T aR · L(b)dΩ
T · bdΩ
» =ε̇–T ·=σdΩ
»=
–
T L
(a)
R
a
Ė
·
Σ
gún la expresión:
Ω· L(b)dΩ
L
(a)
·
bdΩ
Ω
T
Ω
Ω
R Ω R = 1 LT (a) · bdΩ
· L(b)dΩ
R Ω=a N
(z);
=zσxΩ(z)dA
;
σF=(Σ)
σx =
σ(Σ)
=M ;Ω=L
L(σ)dΩ
A(f
(σ))dΩ
»Ω–Σ
» –
A
RM
xˆ
R
˜ �
TodasFellas
aseguran
para
F
el
cumplimiento
F
(Σ)
=
A(f
(σ))dΩ
�
R
∂F
(Σ)
=
A(f
(σ))dΩ
Ω
E
= R FRΩ(Σ)
�=
+ortogonalidad
xc
= 1 »x –
ΛE
» –
=ε =Ωde
A(f
(σ))dΩ
de σ(Σ)
la »
condición
básica
ε̇RT ∂Σ
· σdΩ =
Ė T · Σ » –Nenc
–= cΩ L(σ)dΩ
1
R=
Ω
ˆ
˜
σ(Σ)
L(σ)dΩ
la situación
de flujo
plástico,
expresada
Σ = � por: ; L =
;
σR=R σx (z);
�
Ω
M
x
E R= σ(Σ) = σ(Σ)
ε L(σ)dΩ
=NΩ=
�=
+ ΩxcL(σ)dΩ
=
1
x
σx (z)dA c
c
T
T
A
ε̇ · σdΩ
Ė · Σ T
R T=∂F
Ω R
∂f
RĖΣ
TΛE
=
σdΩ
=
R ·∂Σ
» zσ
–· ΣT
» –
ε̇T Ω· ε̇σdΩ
=
λε
TMĖ= · =
Ω
ˆ
˜ �
ε̇
·
σdΩ
·Σ
A=
∂σ
� Ėx (z)dA
Ω
= estas condiciones
ε = � + xc = 1 x
RE de
∂F
Un ejemplo
conocido
c
c
= ΛE
σx (z)dA
= =A λε
∂FN ∂f
» –
» –
=
ΛE
es el ∂Σ
de∂F
una=sección
de
fábrica
plastificando
∂σ
N
1
∂F
ΛE
Σ=
; L=
;
σ R= σyx (z);
R ∂Σnormales
∂Σ
por tensiones
capacidad
M
= =AΛE
zσxsin
(z)dA
M en
x
N = Aσ
R∂Σ
x (z)dA
R
tracción para
alguna
de∂f
esfuerσRxcombinación
(z)dA
N R=N A=σxA(z)dA
–∂σ = λε» –
N
= A σ»x (z)dA
zosMnormales
y» momentos
–
» –
= A zσ
(z)dA
R
x
1
R
� Σ .=En Neste; L
flectores
caso
zσ
(z)dA
x(z);
= = ˆ1; x˜ �
σRx=
M =M A=σ
zσ=
(z)dA
A
xE
ε
=
�
+
xc
x
M = »A zσ
c
–cx (z)dA»M–
tenemos:
N» –» – 1 » – » –
σ = σx (z); Σ = » – ; LN=» – ; 1 » – » –
MN
;=xL 1= ; ˆ; 1 ˜ �
σx (z);
Σ=
σ =σσx=(z);
�Σ = ; L N
x
=
;xcL =
= 1 x
;
σE==σx (z);MΣ M
ε = �∂f
+x
M =» λε
c
c
» –
– x
∂σ
ˆ
˜ �
� » –» –
» –
»
–
E=
ε = � + xc = 1 ˆ x ˆ ˜ ˜ � » –
�
c � � » –
� +=xc 1= x1c ˆx
E =E = c ε� = ε� =
+ xc
c˜ �
∂f� + xc = c1 x
ε=
cE =
=
λε
c
c
y, definiendo f (s) como el negativo
de la
∂σ
menor diferencia entre
∂f la tensión atribuída
= λε
al punto y la máxima
o la
∂σ ∂fen∂fcompresión
∂fλε
=
λε=
∂σ
tensión nula en tracción,
estableciendo
F
= λε (S)
∂σ
∂σf (s) en tomediante la integral simple de
dos los puntos de la sección, e interpolando,
para obtener una descripción definida de
S (s), las condiciones de solicitación que no
alcancen la rotura como intermedios entre el
estado de compresión centrada mitad de la
máxima y el estado de rotura en la dirección
del alejamiento de los esfuerzos existentes.
Informes de la Construcción, Vol. 62, 518, 33-42, abril-junio 2010. ISSN: 0020-0883. eISSN: 1988-3234. doi: 10.3989/ic.08.045
41
J. Cervera
La última cuestión a considerar responde a
la métrica del espacio en que se representa la función de rotura: es evidente que en
espacios cuyos diferentes ejes corresponden a agregados, las magnitudes o escalas
de cada dimensión pueden no ser comparables en absoluto, lo que hace que medir
en direcciones oblicuas a dichos ejes pueda carecer totalmente de sentido. En estos
espacios, las unidades elegidas deben responder a criterios de incertidumbre, es decir, deben asegurar que una esfera de radio
dado represente en cada dirección una incertidumbre similar en los valores de las
magnitudes representadas. Esto nos remite a la necesidad de validar las escalas
sobre las que se aplica el procedimiento
descrito mediante criterios probabilísticos
que aseguren dispersiones similares para
todas las magnitudes.
En defecto de mayor precisión, la vía empleada aquí responde al procedimiento
habitual de formular los valores de estado
para cada eje en proporción al valor de la
resistencia máxima en dicho eje sin interacción del resto. Para considerar avances en
esta dirección puede resultar útil (4).
REFERENCIAS
(1) D’Ayala, D.F. and Tomasoni, E.: “The structural behaviour of masonry vaults: Limit state analysis with
finite friction”. Structural Analysis of Historic Construction, pages 3 – 19, 2008.
(2) Augusti, G.; Baratta, A. and Casciati, F.: “Probabilistic Methods in Structural Engineering”. Chappman and Hall, London, New York, 1984.
(3) Livesley, R.K.: “Limit analysis of structures formed from rigid blocks”. International Journal for Numerical Methods in Engineering, 12:1853–1871, 1978.
(4) Marti, K. “Limit load and shakedown analysis of plastic structures under stochastic uncertainty”.
Computer Methods in Applied Mechanics and Engineering, 198-1:42 – 51, 2008.
(5) Nielsen, M.P. “Limit analysis and concrete plasticity”. CRC Press, Boca Raton, Florida, 1998. 2ª edición.
***
42
Informes de la Construcción, Vol. 62, 518, 33-42, abril-junio 2010. ISSN: 0020-0883. eISSN: 1988-3234. doi: 10.3989/ic.08.045