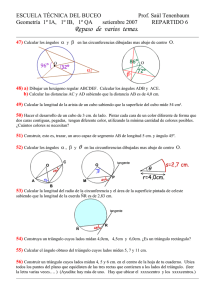
Un ángulo es la región del plano comprendida entre dos

Liceo Bicentenario de Valparaíso
Departamento de Matemática
Profesora Lisette Ugarte Rojas
APUNTES GEOMETRÍA
ÁNGULOS:
Un ángulo es la región del plano comprendida entre dos semirrectas con origen común. A las semirrectas se las llama lados y al origen
común vértice.
Ángulos Adyacentes Complementarios:
Los ángulos adyacentes son ángulos contiguos, que tienen el vértice y un lado común, y suman
90°.
Ángulos Adyacentes Suplementarios:
Dos ángulos adyacentes son ángulos contiguos, que tienen el vértice y un lado común, y los otros
dos lados son semirrectas opuestas. Los ángulos suman 180°.
Ángulos opuestos por el vértice:
Son los ángulos que teniendo el vértice común, los lados de uno son prolongación de los lados del
otro. Los ángulos opuestos por el vértice son iguales.
RECTAS
Rectas paralelas:
Se dice que dos rectas son paralelas cuando no tienen ningún punto en común y siempre están
separadas a la misma distancia, o cuando son coincidentes
Rectas secantes
Se dice que dos rectas son secantes cuando se cortan en un punto.
Rectas perpendiculares:
Se dice que dos rectas son perpendiculares cuando al intersecarse forman cuatro ángulos iguales.
TRIÁNGULOS
Un triángulo es un polígono de tres lados. Sus elementos primarios son los vértices, lados, ángulos interiores y ángulos exteriores
Clasificación de triángulos según la medida de sus lados
Clasificación de triángulos según la medida de sus ángulos
El triángulo equilátero es aquel que tiene todos sus lados de la
misma medida.
El triángulo isósceles es aquel que tiene sólo dos lados de igual
medida.
El triángulo escaleno es aquel que tiene todos sus lados de
distinta medida.
El triángulo acutángulo es aquel que tiene todos sus ángulos agudos.
El triángulo rectángulo es aquel que tiene un ángulo recto.
El triángulo obtusángulo es aquel que tiene un ángulo obtuso.
Elementos secundarios
Altura:
Las alturas de un triángulo son segmentos perpendiculares a los lados del triángulo y que unen
estos con su vértice opuesto (representan la distancia más corta entre el vértice y el lado opuesto).
Se designan con la letra h. Las tres alturas o sus prolongaciones se cortan en un punto llamado
ortocentro (H).
Tips: en un triángulo isósceles la altura dimidia el lado.
Bisectriz:
Las bisectrices son elementos secundarios de un triángulo. Estas dividen cada ángulo interior del
triángulo en dos ángulos de igual medida.
En un triángulo se pueden trazar tres bisectrices correspondientes a sus ángulos interiores. Estas se
intersecan en un punto llamado incentro (I).
Simetrales:
Las simetrales de un triángulo son rectas perpendiculares a los lados del triángulo las cuales pasan
por el punto medio de estos. Se intersecan en un punto llamado circuncentro (C), centro de la
circunferencia circunscrita al triángulo.
Transversal de gravedad:
Las transversales de gravedad son segmentos que unen los puntos medios de cada lado con su
vértice opuesto. Se cortan en un punto llamado centro de gravedad o baricentro (G), que
corresponde al punto de equilibrio del triángulo
Medianas:
Son los segmentos que unen directamente los puntos medios de dos lados del triángulo. La
mediana tiene una longitud igual a la mitad del lado paralelo. Al trazar las tres medianas de un
triángulo, éste queda dividido en cuatro triángulos congruentes.
TEOREMA DE PITÁGORAS
Teorema de Pitágoras: En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a
la suma de los cuadrados de los catetos.
c2 =
a2 + b 2
ÁREA Y PERÍMETRO
Perímetro: Perímetro de un polígono es la suma de todos sus lados, es su contorno.
Área: Es la medida de la superficie de una figura; es decir, la medida de su región interior.
Triángulo
Perímetro
P=a+b+c
Área
A=
Cuadrado:
Perímetro
P=4a
Área
A = a2
Rectángulo:
Perímetro
P = 2 • (b + h)
Área
A=b•h
Rombo:
Perímetro
P=4l
Área
A=
Romboide:
Perímetro
P = 2 • (a + b)
Área
A=b•h
Trapecio:
Perímetro
P=B+b+a+c
Área
A=
Polígono regular:
Perímetro
P=n•l
Área
A=
n = número de lados