71. Una bobina de alambre de 820 vueltas y 24.0Ω de resistencia

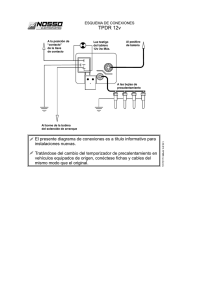
71. Una bobina de alambre de 820 vueltas y 24.0Ω de
resistencia se coloca sobre la parte superior de
un solenoide de 7.0cm de largo y 12500 vueltas,
como en la figura. Tanto la bobina como el
solenoide tienen áreas de sección transversal de
1.0x10-4m2. a) ¿Cuánto tarda la corriente del
solenoide en alcanzar 63.2 por ciento de su valor
máximo? Determine b) la fem inversa promedio
producida por la autoinductancia del solenoide
durante este intervalo, c) la tasa promedio de
cambio en el flujo magnético a través de la bobina
durante este intervalo y d) la magnitud de la
corriente inducida promedio de la bobina.
820 vueltas
24Ω
14Ω
60V
+
12500
vueltas
-
s
DESARROLLO
a) El circuito primario (contiene una batería y un
solenoide) es un circuito RL.
R = 14Ω
L = µ 0N2A
l
L = (4πx10-7T.m/A)(12500)2 (10-4 m2)
0.07m
L = 0.28H
El tiempo de la corriente para alcanzar 63.2% de
su máximo es la constante de tiempo τ
32. INDUTANCIA
τ = L
R
τ = 0.28H
14Ω
τ = 0.02s
b) la fem inversa promedio
<ε> = -L ∆I
∆t
I = 0.63Imax
<ε> = -L (I-0)
t
I = 0.63
60V
14Ω
<εε > = -37.8V
<ε> = -(0.28H) 2.7 A
0.02s
c) B = µ 0nI
B = µ0
N I
l
B = (4πx10-7T.m/A) 12500
0.07m
φ = BA
2.7A
φ = (0.606T)(10-4 m2)
∆φ = 6.06x10-5Tm2
∆t
0.02s
I = 2.7A
B = 0.606T
φ = 6.06x10-5Tm2
∆φ = 3.03x10-3V
∆t
d) El valor de cambio de flujo en la bobina de 820
vueltas es igual que en el solenoide. Por lo
tanto, la magnitud de corriente inducida por la
bobina es:
<ε> = N ∆φ
∆t
<ε> = (820)(3.03x10-3V)
<I> = <ε>
R
<I> = 2.48 V
24Ω
32. INDUTANCIA
<ε> = 2.48V
<I> = 0.104A