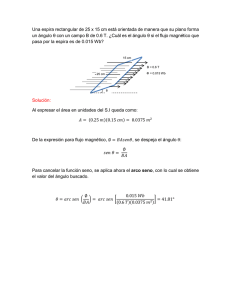
2 División

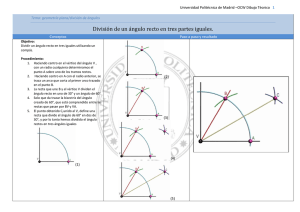
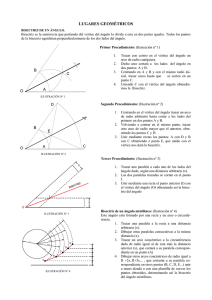
DIVISIÓN DE UN ÁNGULO EN PARTES IGUALES.
B
1
2
Ángulo menor de 180º. (Ilustración nº 1).
1. Prolongar el lado OA una medida igual a su magnitud, obteniendo el punto C, este nuevo segmento AC
nos determina un ángulo llano.
2. Trazar arcos con centros en A y C y radio igual al
segmento AC, que determinan el punto N.
3
4
O
C
5
E
A
3. Unimos el punto B del arco con el punto N mediante
una recta que cortará al segmento AC en el punto E
4. Dividir el segmento AE en tantas partes iguales como se quiera dividir el ángulo, trazar semirrectas de
origen N y que pasen por las divisiones anteriores.
5. Estas semirrectas cortarán al arco del ángulo en diferentes puntos, uniendo estos con el vértice del ángulo quedará dividido este en parte iguales.
Ángulo mayor de 180º. (Ilustración nº 2).
N
1. Efectuar las mismas operaciones realizadas en el
método anterior, en los pasos 1º y 2º.
ILUSTRACIÓN Nº 1
2. Trazar una cuerda al arco del ángulo uniendo los
puntos A y B y hallarle la mediatriz.
3. La mediatriz anterior cortará al arco AB en el punto
D, uniendo este punto con el vértice N mediante una
recta esta cortará al segmento AC en el punto E.
D
5. Llevar la distancia AQ sucesivamente sobre el arco
para dividirlo y unir dichas divisiones con el vértice
O del ángulo, dividiendo este en partes iguales.
2
3
4. Dividir el segmento AE en tantas parte iguales como
queramos dividir el ángulo y unir la segunda división con el punto N mediante una recta, hasta cortar
al arco en Q.
1
4
E
C
Q
5
2 División
O
B
N
ILUSTRACIÓN Nº 2
A