Práctica 2 Propiedades de los sistemas dinámicos

Práctica 2
Propiedades de los sistemas dinámicos
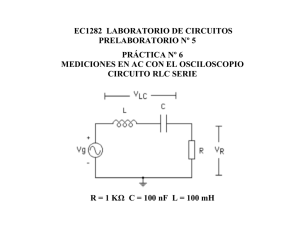
Apartado 1 – Respuesta de un circuito RLC.
El objetivo de esta práctica es realizar un modelo en Simulink de un sistema dinámico, en particular de un circuito
RLC. Este modelo se utilizará para realizar diferentes simulaciones.
a) Realizar un modelo Simulink de el circuito RLC mostrado en la figura 1. Las ecuaciones que definen el comportamiento de una resistencia, una bobina y un condensador son las siguientes:
vr = ir R
l
vl = di
dt L
dvc
ic = dt C
dónde {vr , ir }, {vl , il } y {vc , ic } son la caı́da de tensión y la intensidad que circulan a través de la resistencia, la bobina
y el condensador respectivamente. La entrada del sistema dinámico es la señal V in. La salida del sistema dinámico es
la señal V out (caı́da de tensión en el condensador).
R
L
+
+
Vin
C
Vout
Figure 1: Circuito RLC.
b) Representar la caracterı́stica estática del sistema para V in ∈ [0, 10] [p1].
Utilizar los siguientes parámetros:
V out0 = 4 − DN I(3)
il 0 = 0
t0 = 0
2
3
R = [0.15 + 0.35
10 DN I(2)] DN I(1) 10
1
3
L = DN I(1) 10
C = DN I(1)10−3
Caracterizar la respuesta del sistema en torno a V in = 3 [p2] y V in = 5 [p3]. Utilizar una entrada en escalón de
amplitud 1.
c) Representar la caracterı́stica estática del sistema para V in ∈ [0, 10] [p4].
Utilizar los siguientes parámetros:
V out0 = 4 − DN I(3)
il 0 = 0
t0 = 0
2
3
R = [1 + 0.5
10 DN I(2)] DN I(1) 10
L = DN1I(1) 103
C = DN I(1)10−3
Caracterizar la respuesta del sistema en torno a V in = 3 [p5] y V in = 5 [p6]. Utilizar una entrada en escalón de
amplitud 1.
1
Apartado 2 – Estudio de un sistema mediante simulación.
Dado el sistema no lineal incluido en el archivo “sistema.mdl”, se pide:
a) Hallar experimentalmente (sin utilizar expresiones analı́ticas) la caracterı́stica estática del sistema, utilizando un
rango de valores en la entrada entre 0 y 10 [p7].
b) Estudiar la respuesta temporal del sistema en torno a los siguientes puntos de operación: U=3 [p8], U=7 [p9]y
U=0 [p10]. Utilizar una entrada en escalón de amplitud 1.
Apartado 3 – Cuestiones
C1) ¿Afectan los valores de R, L y C a la caracterı́stica estática de un circuito RLC?
C2) ¿Afectan los valores de R, L y C a la respuesta transitoria de un circuito RLC? ¿Cómo afecta cada uno de los
parámetros? Realizar diferentes simulaciones para responder a esta pregunta.
C3) ¿Afectan los valores de R, L y C a la respuesta transitoria de un circuito RLC?
C4) ¿Afecta el punto de trabajo a la respuesta transitoria de un circuito RLC?
C5) ¿Afecta el punto de trabajo a la respuesta transitoria del sistema descrito por el modelo “sistema.mdl”?
Apartado 4 – Instrucciones para entregar el módulo usando el Servidor de Docencia.
Los resultados se entregarán usando Goodle GMC. Se podrá acceder a Goodle durante toda la semana que dure
cada práctica. La entrega de la práctica a través del servidor consiste en rellenar el formulario de texto siguiendo las
siguientes instrucciones:
• Cada respuesta correspondiente a una cuestión de trabajo en el centro de cálculo tiene asignado un nombre. En
el enunciado de la práctica se indica con una etiqueta entre corchetes cada respuesta que hay que entregar.
• Para las respuestas p1, p4 y p7 hay que definir una matriz de dos filas y 10 columnas. En la primera fila se
almacena el valor de la entrada y el la segunda fila el valor correspondiente de la salida en régimen permanente.
Si el sistema se hace inestable el valor en régimen permanente es Inf.
Ejemplo:
p1 = [1 2 3 4 5 6 7 8 9 10; 0.3 0.6 0.8 1.4 1.6 4.5 7.8 10.2 Inf Inf];
• Para el resto de respuestas hay que definir un vector con la siguiente estructura:
p1 = [es L K ts tr tp te Mp]
El componente es indica si el sistema es estable (es = 1) o inestable (es = 0).
El resto de componentes indican el retraso L, la ganancia K, el tiempo de subida ts, el tiempo de levantamiento
tr, el tiempo de pico tp, el tiempo de establecimiento te y el sobrepaso Mp (en tanto por uno).
Si la respuesta es sobreamortiguada tr, tp, y Mp valen 0.
Si la respuesta es subamortiguada ts vale 0.
Ejemplo:
p2 = [1 0 1 3 0 0 0 0];
p3 = [1 0 1 0 1.2 2.4 5 0.4];
Entrega
La entrega consiste en una memoria de la práctica en un fichero pdf y la entrega de resultados. La memoria debe
contener:
• Imagen de los modelos de Simulink utilizados.
• Figura con las caracterı́stica estáticas y las respuestas transitorias estudiadas.
• Respuesta a las cuestiones.
2