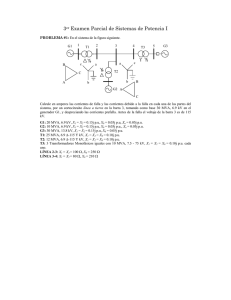
Un transformador de 60 MVA alimenta mediante una línea larga dos

Circuitos Magnéticos y Transformadores
Problema 4.8
Un transformador de 60 MVA alimenta mediante una línea larga dos transformadores,
uno de 30 MVA y otro de 25 MVA.
Los datos de los transformadores son los siguientes:
TRANSFORMADOR DE 60 MVA: 132/45 kV, grupo de conexión Yyd, impedancia de
cortocircuito porcentual 11%. Pérdidas en el cobre a plena carga 248 kW. Pérdidas en el
hierro 45 kW
TRANSFORMADOR DE 30 MVA: 45/15 kV, conexión Yd, impedancia de
cortocircuito porcentual 10%. Pérdidas en el cobre a plena carga 105 kW
TRANSFORMADOR DE 25 MVA: 45/15 kV, conexión Dy, impedancia de
cortocircuito porcentual 9%. Pérdidas en el cobre a plena carga 92 kW
Línea: Impedancia de la línea: 0,5 /km. Longitud 4 km. Se considera inductiva pura
En un momento determinado el transformador de 30 MVA funciona al 60% de carga
con factor de potencia 0,85 inductivo y el transformador de 25MVA funciona al 45% de
carga con un factor de potencia 0,9 inductivo 1. La tensión en la red de 132 kV oscila a
lo largo del día, y en el instante de tiempo considerado la tensión de dicha red es 140
kV.
Se pide:
1) Calcular la tensión en bornas del transformador de 25 MVA
2) Factor de potencia que presenta el transformador de 60 MVA a la red de
alimentación
3) En el supuesto caso de que el transformador de 30 MVA esté en vacío y que la
red de 132 kV2 tenga una potencia de cortocircuito de 7.200 MVA calcular la
corriente de cortocircuito en caso de un cortocircuito en bornas del
transformador de 25 MVA
4) Rendimiento del transformador de 60 MVA.
1
Aunque no es estrictamente cierto, admítase que el factor de potencia indicado es respecto de la tensión
de alimentación a la red de 132 kV (esto es 140 kV)
2
La red de tensión nominal 132 kV, si bien en el instante de tiempo considerado la tensión vale 140 kV
Juan Carlos Burgos
Universidad Carlos III de Madrid
1
Circuitos Magnéticos y Transformadores
Problema 4.8
SOLUCIÓN:
Trafo T1: 60 MVA
 U 2 11·132 2
Z ccY  cc L 
 31,94
100S N 100·60
I1N 
RccY
SN

60·10 6
 262,43 A
3132·103
3U1N
P
 cc2  1,2
3I N
2
2
X ccY  Z ccY
 RccY
 31,92
Trafo T2: 30 MVA
 U 2 10·452
Z ccY  cc L 
 6,75
100S N 100·30
I1N 
RccY
SN

30·10 6
 384,9 A
3·45·103
3U1N
P
 cc2  0,236
3I N
2
2
X ccY  Z ccY
 RccY
 6,75
Pasamos la impedancia al lado de 132 kV
2
 132 
R'ccY  RccY rt  0,236
  2,03
 45 
X 'ccY  X ccY rt 2  58,08
2
Trafo T3: 25 MVA
 U2
9·452
Z ccY  cc L 
 7,29
100S N 100·25
I1N 
RccY
SN

25·10 6
 320,75 A
3·45·103
3U1N
P
 cc2  0,298
3I N
2
2
X ccY  Z ccY
 RccY
 7,28
Pasamos la impedancia al lado de 132 kV
2
 132 
R'ccY  RccY rt  0,298
  2,56
 45 
X 'ccY  X ccY rt 2  62,64
2
Juan Carlos Burgos
Universidad Carlos III de Madrid
2
Circuitos Magnéticos y Transformadores
Problema 4.8
Línea

 132 
X 'Línea  
4km  17,21
 0,5
km
 45 
2
Carga transformadores
I T 2  kT 2 I NT 2  0,6·384,9  230,94 A
I T 3  kT 3 I NT 3  0,45·320,75  144,34 A
La intensidad que circula por el transformador T1 (de 60 MVA) es la suma de la que
entrega al transformador T2 (de 30 MVA) y la que entrega al transformador T3 (de 25
MVA)
I T 1  I T 2  I T 3  78,73  31,79  49,21  25,84
I T 1  I T 2  I T 3  111,21  j 62,92  127,77  29,50
Apartado 2: Factor de potencia
cos   cos(29,50)  0,87 ind
Apartado 1: Tensión en bornas del trafo T3
La corriente que circula por el transformador T1 es diferente a la que circula por el
transformador T3, por eso haremos el apartado en dos partes: Primero obtendremos la
tensión en el lado de AT del trafo de 30 MVA y luego la tensión en el lado de BT del
mismo trafo.
Tensión en el lado de AT de los trafos T2 y T3
U ATfnT 3  U1 fn  ( Z ccT 1  Z 'Línea ) IT 1 
140·103
 (1,2  j31,92  j17,21)·127,77  29,50
3
U ATfnT 3  77.792V  3,97
Tensión en el lado de BT del trafo T3
U 'BTfnT 3  U ATfnT 3  ZccT 3 IT 3  77792  3,97  62,7387,66·49,21  25,84
U 'BTfnT 3  76.579V  6,08
U 'BTLineaT3  76.579· 3  132.638V
 15000 
U BTLineaT3  132.638·
  15.073 V
 132000 
Apartado 3: Corriente de cortocircuito
En primer lugar se ha de calcular la impedancia de la red, que se admite inductiva pura
Juan Carlos Burgos
Universidad Carlos III de Madrid
3
Circuitos Magnéticos y Transformadores
Scc  3U1NL I cc  3U1NL
U1Nfn
Z Re d

Problema 4.8
U12NL
Z Re d
Por tanto
Z Re d 
U12NL 1322

 2,42 
Scc
7200
La corriente de cortocircuito pedida es
I cc 
( Z Re d
140000
U1Nfn
3

 Z ccT 1  Z L  Z ccT 3 ) j 2,42  1,2  j 31,92  j17,21  2,56  j 62,64
140000
140000
3
3
I cc 

 707,48  88,1º
3,76  j114,19 114,2588,1º
Apartado 4: Rendimiento del transformador de 60 MVA.

P2
P2  PFe  Pcu
Tensión en bornas del secundario del trafo de 60 MVA
140·103
U 'BTfnT1  U1 fn  Z ccT 1IT 1 
 31,9487,85·127,77  29,50
3
U 'BTfnT1  78.765V  2,53
P2  3·78.765·127,77·cos(2,53  29,50)  26.907.918 W
De forma más sencilla, hubiéramos podido obtener P 2 de la forma siguiente:
P2  Pcu  3·140.000·127,77·cos(29,50)  26.965.864 W
P2  26.965.864  Pcu  26.965.864  3·1,2·127,772
P2  26.965.864  58.771  26.907.093 W
La diferencia entre los dos cálculos es debida al redondeo de operaciones.

P2
26907918

 99,62 %
P2  PFe  Pcu 26965864  45000
Juan Carlos Burgos
Universidad Carlos III de Madrid
4