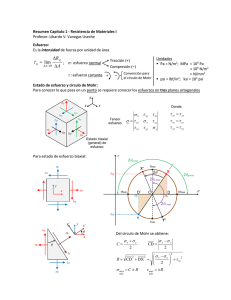
Ejercicios de Circulo de Mohr

Ejercicios de Circulo de Mohr
Procedimientos y convenciones:
En plano físico:
-
-
Graficar estado tensional del punto en un elemento cuadrado (tensiones
normales y de corte) según convención de signos (eje horizontal y vertical
siguiendo el orden menor a mayor)
Las tensiones de tracción son positivas y de compresión negativas
Sentido positivo de ángulos desde eje menor a mayor (ej: x2 a x3)
La dirección de máxima tensión (sin corte en el plano) será cercana a la indicada
por la tensiones de corte, la cual será atraída por tensiones normales de tracción
y alejada por tensiones de compresión (utilizar esta estimación a priori para
verificar resultado)
En círculo de Mohr:
-
-
Ejes de tensiones normales y de corte
Graficar el primer punto (punto 0, con su valor de tensión normal y de corte)
Graficar el (punto P, con su valor de tensión normal y para la tensión de corte
cambiar el signo)
La dirección en el círculo de Mohr desde punto 0 a punto P define la dirección
del eje correspondiente al punto P en el plano físico (ej: si el punto 0
corresponde a σ11 y el punto P corresponde a σ33 , entonces la dirección 0P
corresponde al eje x 3 en el plano físico)
Encontrar valores de tensión media (centro de círculo) y radio, luego de tensión
normal máxima y mínima, de corte máxima
El valor del ángulo desde el polo es la mitad de ángulo desde centro de círculo
(por geometría)
Sentido de ángulos es al revés del plano real (si en circulo de Mohr es horario en
plano real será antihorario)
En plano físico:
-
-
Trazar la dirección de tensión máxima (partir desde el eje de referencia y tener
en cuenta sentido opuesto a circulo de Mohr) y verificar que concuerde con la
dirección estimada a priori
El plano físico de rotura es perpendicular a la dirección de falla que se determinó
mediante el círculo de Mohr (ej: criterio de Mohr-Coulomb).
Ejemplo 1:
0
0 0

σij = 0 −10 40 
0 40 20 
Eje x1 es principal porque no tiene
tensiones de corte
σ + σ33 −10 + 20
σm = 22
=
=5
2
2
 2.40 
1
ϕmax = a tan 
 = −34.72º
2
 20 − ( −10 ) 
(Signo negativo por convención)
2
R = σ 232 + ( σ 22 − σ m ) = 40 2 + ( −10 − 5 )
2

0
  0 


ν max =  −sen ( ϕmax )  =  0.569 
= 42.72  cos ( ϕ )   0.822 
max 



σmax = σ m + R = 42.72 + 5 = 47.72
Verificación:
σνν = σijν i ν j = −10x0.5692 + 2x40x0.569x0.822 + 20x0.8222 = 47.72
El valor de la tensión normal para el plano definido por el versor ν max corresponde al
calculado con el círculo de Morh
1 
0 
0   0 




σν = σijν i t j = 0  0  + ( −10x0.569 + 40x0.822 ) 1  + ( 40x0.569 + 20x0.822 ) 0  =  27.18
 0 
0 
1  39.22 
σν = σν1 2 + σν2 2 + σν2 2 = 42.72
σνs =
2
σν − σνν 2 = 0
El valor de la tensión de corte para el plano definido por el versor ν max es nulo
Ejemplo 2:
 30 −5 0 
σij =  −5 10
0 
 0 0 −20 
Eje x 3 es principal porque no tiene tensiones de corte
σ + σ22 30 + 10
σm = 11
=
= 20
2
2
2
2
R = σ12 2 + ( σ11 − σ m ) = 52 + ( 30 − 20 ) = 11.18
σmax = σ m + R = 20 + 11.18 = 31.18
1
1
20 − 10  
( 90 + α ) =  90 + a tan 
  = 76.71º (Signo positivo por convención)
2
2
 5 
 −sen ( ϕmax )   −0.9732 


=  cos ( ϕmax )  =  0.2298 

  0 
0
ϕmax =
ν max
Ejemplo 3:
 −15 0 −10 
σij =  0 25 0 
 −10 0 −35 
Eje x 2 es principal porque no tiene tensiones de corte
σ + σ33 −15 − 35
σm = 11
=
= −25
2
2
2
R = σ132 + ( σ11 − σ m ) =
2
( −10 ) + ( −15 − ( −25 ) )
2
= 14.14
σmax = σ m + R = −25 + 14.14 = −10.86
ϕmax =
ν σmax
1
1
35 − 25  
( 90 + α ) =  90 + a tan 
  = 67.5º (Signo positivo por convención)
2
2
 10  
 − sin ( ϕmax )   −0.924 

 

=
0
= 0 
 cos ( ϕmax )   0.383 
Ejercicios:
-
Verificar que la dirección definida por el versor ν max de una tensión normal
igual al círculo de Mohr.
Calcular el tensor de tensiones rotando los ejes x1 y x 3 el ángulo calculado y
verificar que no aparezcan tensiones de corte en el tensor de tensiones (ejes
principales)