Transmisión Digital Paso Banda Transmisión Digital Paso Banda

Tr ansmisión Digital Paso Banda
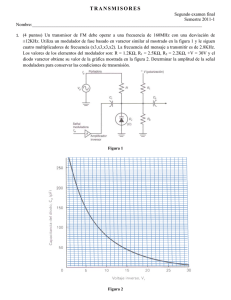
PRÁCTICA 9
(2 sesiones)
Laboratorio de Señales y Comunicaciones
3er curso, Ingeniería de Telecomunicación
Javier Ramos, Fernando Díaz de María y David Luengo García
1. Objetivos
Simular un sistema de comunicaciones sencillo en el que únicamente se consideren las
diferentes técnicas de modulación paso banda. En concreto, se pretenden revisar los
siguientes aspectos:
1. Los diversos esquemas de modulación paso banda binarios (BASK, BPSK y
BFSK) y sus mecanismos de generación.
2. La estructura de los receptores óptimos (coherentes) y la importancia de una
correcta recuperación de la fase (sincronismo).
3. Las diferentes estructuras de los receptores subóptimos.
2. Contenido teórico
2.1. Sistema de comunicaciones digitales paso banda
El esquema de un sistema de comunicaciones paso banda es el mismo que el de
un sistema en banda base: los bits que se desean transmitir se usan para modificar algún
parámetro de una forma de onda adecuada con las características del canal (una sinusoide habitualmente), esta señal modulada se transmite a través del canal, que puede
introducir distorsión (dando lugar a ISI) y ruido (modelado normalmente como blanco,
aditivo y Gaussiano), y por último el receptor óptimo estima los bits transmitidos
mediante un filtro adaptado, un muestreador, y un detector de umbral.
El modulador es el elemento central del sistema, y el que se va a estudiar en esta
práctica. En general las señales transmitidas van a ser de la forma
xc (t ) = A(t ) cos(" c t + ! (t )) ,
de modo que existen tres parámetros que se pueden modificar para transmitir la información deseada: amplitud, fase y frecuencia. En función de cuál de estos parámetros de
la señal portadora, xc(t), contenga la información transmitida, se tienen las distintas
técnicas de modulación. Si la información se envía en la amplitud se tiene un modulador
del tipo ASK (Amplitude Shift Keying), si se transmite en la fase se habla de PSK
(Phase Shift Keying), si se codifica en la frecuencia el esquema se denomina FSK
(Frequency Shift Keying), y por último cuando se combina una modulación de amplitud
y fase se conoce como APK (Amplitude Phase Keying).
La manera más habitual de expresar una señal de comunicaciones digitales paso
banda es mediante la combinación de una serie de funciones base ortonormales:
N
L
x(t ) = !! ai [n]#i (t " nT ) ,
n =0 i =1
donde T es el periodo de símbolo, φi(t) representa a cada una de las L funciones base, y
ai[n] es la amplitud que toma la función base i-ésima durante el intervalo n-ésimo en
función del símbolo que se desee transmitir. Nótese que esta expresión es simplemente
una generalización de la mostrada en la práctica anterior para las señales PAM en banda
base, para las cuales L = 1 (es decir, sólo existía una función base, el pulso base). Las
dos funciones base más habituales son el coseno y el seno,
"1 (t ) =
2
cos(! c t ) ,
T
"2 (t ) =
2
sin(! c t ) .
T
De hecho, como se muestra a continuación, todos los sistemas propuestos
anteriormente, con excepción del FSK, se pueden expresar usando estas dos únicas
funciones base:
N
x(t ) = ! (a1 [n]#1 (t " nT ) + a2 [n]#2 (t " nT ) ).
(1)
n =0
2.1.1. M-ASK
La técnica de modulación digital paso banda más sencilla es la M-ASK. En este
esquema la información se envía seleccionando una amplitud diferente para cada uno de
los M posibles símbolos, de modo que las posibles formas de onda son
2 Ei
cos(! c t ),
T
si (t ) =
con 0 ! t ! T , y 1 ! i ! M . Está claro que en esta ocasión sólo se emplea una función
base, φ1(t), y su amplitud, a1 [n]!
{ E ,K,
1
}
E M , depende directamente del símbolo a
transmitir. Para el caso binario por ejemplo, se toman habitualmente E1=0 y E2= E s ,
de modo que
N
x(t ) = E s ! (s[n]" 1)#1 (t " nT ) .
n =0
Este esquema, que transmite un fragmento de señal cuando se desea enviar un uno, y
nada cuando se desea enviar un cero, también se conoce como OOK (On-Off Keying).
2.1.2. M-PSK
Para el esquema de modulación M-PSK se envía una de las M formas de onda
siguientes:
si (t ) =
2Es
2'i #
&
cos$ ( c t +
!,
T
M "
%
con 0 ! t ! T , y 1 ! i ! M . Utilizando las relaciones trigonométricas estas formas de
onda se pueden reescribir como
( 2"i %
( 2"i %
si (t ) = E s cos&
#!1 (t ) ) E s sin &
#!2 (t ) ,
'M $
'M $
de modo que resulta evidente que las señales M-PSK se pueden expresar mediante la
ecuación (1), con unos coeficientes
& 2' s[n]#
a1 [n]= E s cos$
!,
% M "
& 2( s[n]#
a2 [n]= ' E s sin $
!,
% M "
donde s[n] indica el símbolo que se desea transmitir de entre los M posibles
( 1 ! s[n]! M ). El caso binario (2-PSK o BPSK) presenta la particularidad de que
a1[n]=±1 y a2[n]=0, y en consecuencia la señal transmitida se puede expresar como:
N
s [n ]
x(t ) = E s ! (" 1) #1 (t " nT ) .
n =0
2.1.3. M-FSK
El último esquema de modulación paso banda que se va a considerar es M-FSK.
En esta técnica de modulación cada símbolo se transmite usando una portadora con una
frecuencia distinta. En consecuencia, existen M funciones base diferentes (una para
cada símbolo a transmitir) y la señal transmitida es:
N
x(t ) = E s ! # s [n ](t " nT ) ,
n =0
donde s[n] indica el símbolo a transmitir, 1 ! s[n]! M , y las funciones base son:
"i (t ) =
2
cos(!i t ).
T
2.3. Transmisión por el canal y recepción de las señales
La señal generada por el modulador se va a transmitir a través de un canal
compuesto por dos elementos: un sistema lineal y ruido aditivo blanco Gaussiano
(AWGN). El esquema del sistema de comunicaciones digitales paso banda es idéntico al
de banda base (véase la Figura 1). El sistema lineal en esta práctica va a ser
simplemente un filtro paso banda, que va a simular la limitación en ancho de banda de
cualquier canal real. El ruido se suele caracterizar mediante su densidad espectral de
potencia (DEP) que, al ser blanco, es constante e igual a No/2 para cualquier frecuencia.
Nuevamente la potencia de ruido en el receptor dependerá de su ancho de banda (¡¡no
del ancho de banda del canal!!), que en un receptor implementado de manera discreta en
Matlab es la mitad de la frecuencia de muestreo, igual que en la práctica 8.
Figura 1: Esquema simple de un sistema de comunicaciones digitales.
El receptor óptimo para cualquier esquema de modulación está formado por los
mismos tres elementos que para la transmisión en banda base: un filtro adaptado, un
muestreador y un detector de umbral. El filtro adaptado es el primer bloque del
receptor, y su objetivo es maximizar la relación señal a ruido a su salida cada T
segundos. En este caso, puesto que se transmite usando L funciones base ortonormales,
va a ser necesario disponer de L filtros adaptados: uno asociado a la forma de onda de
cada una de ellas, hi (t ) = "i (T ! t ) . A continuación el muestreador se limita simplemente a quedarse con una muestra por símbolo a la salida del filtro adaptado (igual que
en banda base), ya que no son necesarias más muestras para el proceso de detección. El
esquema del filtro adaptado más el muestreador se representa en la Figura 2. Por último,
el detector decide si el bit enviado ha sido un 0 o un 1 en función de un umbral.
Figura 2: Filtro adaptado a φ(t) y muestreador.
Los receptores óptimos que siguen la estructura descrita anteriormente se suelen
denominar coherentes, ya que requieren la estima de la fase de la señal recibida. Para
casi todos los esquemas de comunicaciones paso banda también se pueden desarrollar
receptores no coherentes, que no requieren estimar la fase de la señal recibida. Aunque
estos receptores presentan un peor rendimiento (típicamente son necesarios 3 dB
adicionales de Eb/No para obtener la misma probabilidad de error) su implementación
suele ser mucho más sencilla que la de los coherentes. La estructura de estos receptores
depende en gran medida de la técnica de modulación empleada, de modo que su
esquema se discutirá a lo largo de la práctica cuando sea necesario.
3. Cuestionario previo
3.1. Dada la secuencia binaria b = {1, 0, 0, 1, 1, 0, 0, 0, 1, 1}, dibuje la forma de onda
generada por cada una de las siguientes técnicas de modulación paso banda:
a) BASK.
b) BPSK.
c) BFSK.
d) QPSK.
3.2. Obtenga la expresión de la densidad espectral de potencia (DEP) de una señal
BASK, BPSK y BFSK utilizando como base la DEP de una señal PAM en banda
base obtenida en la práctica anterior, y el diagrama de bloques de los distintos
moduladores mostrado en las Figuras 3, 4 y 5.
3.3. Deduzca las fórmulas para la probabilidad de error de cada uno de los esquemas
de modulacion de la cuestión 3.1 (puede hacerlo a partir de sus constelaciones
viendo la distancia entre símbolos para cada uno de ellos), y rellene la Tabla 1.
Eb/No
BASK
BPSK
QPSK
BFSK
0
2
4
6
8
10
Tabla 1: Probabilidad de error (teórica) para diferentes técnicas de modulación.
4. Transmisión y recepción paso banda
Al igual que en la práctica 8, en esta práctica es necesario inicializar una serie de
variables globales mediante la ejecución del programa start antes de la evaluación del
resto de los programas. El programa start solamente necesita ejecutarse una vez al
comienzo de la sesión (asegúrese de que dispone de la versión adecuada). Las
principales variables inicializadas por esta función son:
1. La tasa binaria, BINARY_DATA_RATE = 1000.
2. El factor de muestreo, SAMPLING_CONSTANT = 100.
3. La frecuencia de muestreo:
SAMPLING_FREQ = BINARY_DATA_RATE · SAMPLING_CONSTANT.
Características de las diferentes técnicas de transmisión paso banda
Ejercicio 4.1. La técnica de modulación paso banda más sencilla posiblemente sea la
BASK, en la que para los unos se envía un fragmento de una sinusoide con una
amplitud A=1, y para los ceros no se envía señal (este esquema también se conoce como
On-Off Keying, OOK). El esquema básico de un modulador BASK es el siguiente:
t
t
101001
Codificador
NRZ unipolar
sin( 2! f c t )
Figura 3: Diagrama de bloques de un modulador BASK “unipolar”.
Nótese que primero se codifica la secuencia de bits con un codificador NRZ
unipolar, y a continuación se multiplica por la portadora (en este caso un seno). En este
ejercicio se le pide que implemente un modulador BASK mediante el uso de las
funciones wave_gen, ya vista en prácticas anteriores, mixer(x,y), que simula el
comportamiento de un mezclador perfecto, proporcionando a su salida el producto
muestra a muestra de los vectores x e y, y osc(fc,N), que genera N muestras de una sinusoide de la frecuencia deseada, fc. Compruebe el correcto funcionamiento del modulador
generando un vector con 10 bits aleatorios, modulándolos (con fc=8 KHz) y visualizando la salida del codificador NRZ y de la señal modulada paso banda. ¿Cuáles son la
energía y la potencia media por bit de las señales transmitidas?
Ejercicio 4.2. Utilizando la función psd(x,frec_range) visualice la densidad espectral de
potencia (DEP) de la señal modulada (genere 1000 bits en esta ocasión). El parámetro
frec_range es un vector de dimensión 1 × 2 cuyos elementos definen la frecuencia
inicial y final de presentación de la DEP respectivamente. En caso de no pasarle el
parámetro frec_range, la función psd(x) presenta la PSD entre 0 y la mitad de la
frecuencia de muestreo. Visualice la densidad espectral de potencia entre 0 y 50KHz
primero, amplíe la zona entre 0 y 20KHz, y luego vea el detalle entre 5 y 11KHz.
Compare este espectro con el de la señal unipolar NRZ, y anote las características más
significativas de la DEP de la señal modulada: ancho de banda (entre los dos primeros
ceros), nivel del lóbulo principal y del primer lóbulo secundario, y posición de los ceros.
Ejercicio 4.3. Se puede generar una señal BPSK de manera similar a la señal BASK,
cambiando simplemente el codificador NRZ unipolar por otro polar. La estructura del
modulador y las señales generadas se muestran en la Figura 4.
t
101001
t
Codificador
NRZ polar
sin( 2! f c t )
Figura 4: Diagrama de bloques de un modulador BPSK.
Repita los ejercicios 4.1 y 4.2 para un modulador BPSK: genere 10 bits
aleatorios y compare las formas de onda de señal NRZ polar codificada y la señal
BPSK, a continuación, calcule la DEP de la señal BPSK (usando 1000 bits), compárela
con la de la señal NRZ, y anote sus principales características (de la señal BPSK).
Calcule de nuevo la potencia y la energía media por bit de la señal transmitida.
Ejercicio 4.4. Por último, una señal BFSK se puede generar también con la ayuda de un
codificador NRZ polar más un oscilador controlado por tensión (VCO). El esquema de
un modulador BFSK y las señales generadas se muestra en la Figura 5.
t
101001
Codificador
NRZ polar
t
VCO
k Hz/V
Figura 5: Diagrama de bloques de un modulador BFSK.
Para implementar el VCO en Matlab, se ha desarrollado la función vco(xbb),
donde xbb es la señal en banda base proporcionada por el codificador NRZ. Repita el
ejercicio 4.3 para el modulador FSK. Es decir, programe el modulador FSK y estudie la
señal generada tanto en el dominio como en el de la frecuencia (DEP), anotando sus
principales características y comparándolas con las de la codificación NRZ polar. A la
vista de los resultados, ¿cuál debe ser la separación mínima entre la frecuencia
correspondiente al cero y al uno? ¿cuáles son la energía y la potencia media por bit de la
señal FSK transmitida?
Recepción coherente (óptima)
Ejercicio 4.5. En la Figura 6 se muestra el diagrama de bloques de un demodulador
coherente para BASK y BPSK (es decir, esquemas de transmisión que utilizan una
única función base).
r(t)
Filtro Adap.
sin (2! f t )
Figura 6: Diagrama de bloques de un receptor coherente de BASK o BPSK.
En este ejercicio se le pide que implemente este receptor. Para ello, primero
codifique las funciones matched2(‘tipo_de_codigo’) y muestras2(ym,instant_muest),
que son una generalización de las de la práctica anterior en las que se lee la variable
global SAMPLING_CONSTANT para averiguar el factor de sobremuestreo en lugar de
asumir que este es 10 (para poder usar una variable global dentro de una función
primero es necesario declararla con global variable). El resto de funciones necesarias
(osc, mixer y detect) ya se encuentran disponibles de esta práctica o la anterior. Los dos
únicos parámetros que faltan por estimar son instant_muest para la función muest2 y
umbral para la función detect. Ambos se pueden estimar mediante el diagrama de ojo a
la salida del filtro adaptado. Para comprobar el correcto funcionamiento del receptor,
use 1000 bits aleatorios y compruebe que la probabilidad de error de recepción es cero.
Nota: Es recomendable desarrollar los receptores de BASK y BPSK en dos funciones
(por ejemplo rx_bask y rx_bpsk) para poder usarlos en los ejercicios 4.7.
Ejercicio 4.6. Utilizando las mismas funciones que en el apartado anterior construya un
receptor de BFSK (usando la función rx_bfsk por ejemplo). Note que en este caso son
necesarios dos filtros adaptados, uno por cada una de las dos frecuencias transmitidas, y
dos muestreadores. ¿Cómo construiría el detector utilizando la función detect de la que
dispone y cuál sería el umbral de detección? Para comprobar el correcto funcionamiento
del receptor, use 1000 bits aleatorios y compruebe que la probabilidad de error de
recepción es cero.
Ejercicio 4.7. La mayor dificultad en la realización de receptores coherentes es la
sincronización de la portadora. Para que la demodulación sea óptima, la fase y
frecuencia de la sinusoide generada en el receptor tienen que ser idénticas a la fase y
frecuencia de la señal recibida. Pequeños errores en la estimación de la fase y/o la
frecuencia conllevan grandes degradaciones de las prestaciones del sistema de comunicaciones. En este ejercicio se va a simular un error de sincronismo en un receptor
coherente y se van a estudiar sus efectos.
Para ello genere 10000 bits aleatorios, codifíquelos usando el modulador BASK, y pase
la señal resultante por un canal de comunicaciones de amplitud unidad, ancho de banda
20 KHz, y potencia de ruido 5 W. Modifique el programa del receptor para incluir un
error de sincronización fijo (la fase del oscilador del receptor se puede modificar
mediante el tercer parámetro de la función osc), y compruebe como aumenta la
probabilidad de error de bit en el sistema completo conforme se incrementa el desfase
entre la portadora y el oscilador local del receptor. Repita el cálculo para los sistemas
BPSK y BFSK y rellene la Tabla 3 (página siguiente). ¿Qué probabilidad de error se
obtiene cuando el error de fase es de 90 º? ¿Es lo que esperaba obtener? Razone su
respuesta.
Nota: Nuevamente tiene que tener en cuenta el retardo introducido por el canal y
compensarlo del modo descrito en el ejercicio 4.8 para obtener los resultados esperados
(es decir, que la menor probabilidad de error se de cuando el error de fase sea nulo).
Error de fase
Pe (BASK)
Pe (BPSK)
Pe (BFSK)
(grados)
0
5
10
20
30
50
70
90
Tabla 3: Probabilidad de error en función del error de fase.
Recepción no coherente (subóptima)
Ejercicio 4.8. Un posible receptor no coherente para un sistema de modulación BASK
consiste en un simple detector de envolvente (es decir, un detector de la presencia o no
de señal) seguido de un muestreador y un detector de umbral, como se muestra en la
Figura 7.
y(t)
Detector
de
Envolvente
z(t)
Figura 7: Diagrama de bloques de un receptor no coherente de BASK.
La única función nueva que resulta necesaria para construir este receptor es
envelope(entrada, frec_corte), que simula el detector de envolvente con una frecuencia
de corte frec_corte. En esta ocasión, como el primer nulo del espectro de la señal
demodulada esta en 1 KHz (Rb), utilice una frecuencia de corte de 1 KHz. Además, se
deben calcular de nuevo el instante de muestreo óptimo y el valor del umbral a partir del
diagrama de ojo a la salida del detector de envolvente (utilice el segundo ojo), de
manera similar a como se hizo en el ejercicio 4.5. En este ejercicio se le pide que
desarrolle una función que implemente dicho receptor no coherente (por ejemplo
b_est=rx_bask_envolv(x)), que calcule su probabilidad de error para valores de Eb/No
entre 10 y 24 dB (con paso de 2 dB), y que lo compare con los resultados de la primera
columna de la Tabla 2. Intente evaluar el incremento en Eb/No necesario para obtener la
misma probabilidad de error que el receptor coherente.
Nota: A la hora de calcular la probabilidad de error debe tener en cuenta que algunos de
los últimos bits de información pueden no haberse llegado a simular por el truncamiento
que efectúa la función envelope, de modo que hay que descartarlos para evitar errores.