Proyectos 1.- Definir un predicado “aplanadora” que permita

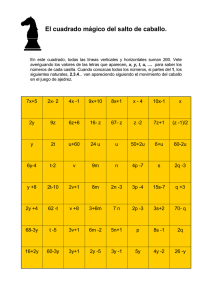
Proyectos
1.- Definir un predicado “aplanadora” que permita aplanar una lista con listas de tal forma
que la nueva lista generada no contenga sublistas, únicamente elementos, es decir,
conteniendo todos los elementos que originalmente están contenidos en la lista original.
Ejemplo.
 aplanadora([a, [b, c], [[d], [], e]], X).
X = [a, b, c, d, e]
Nota: Existen al menos 6 formas diferentes de programar este predicado.
2.- El problema del caballo (Figura 1) es un antiguo problema matemático en el que se pide
que, teniendo una cuadrícula de 8 x 8 casillas y un caballo de ajedrez colocado en una
posición cualquiera ( x, y ), el caballo pase por todas las casillas y una sola vez.
Lo que resulta en n2-1 movimientos.
Figura 1. Problema del caballo (recorrido total del tablero)
3.- Desarrollar un programa en prolog que dadas las definiciones de al menos 10 figuras
similares a las mostradas en la siguiente figura pueda resolver el algoritmo siguiente:
A debe ser el inverso de B. Eso implica que debemos calcular el inverso de C. Si el inverso
de C está en la lista de respuestas, hemos encontrado la respuesta. En caso contrario,
volvemos al paso 2 para encontrar otra solución.
Figura 2. Ejemplos de figuras inversas
4.- Construya un programa prolog para armar el rompecabezas cuyas fichas se muestran en
la figura 3. Defina una estructura para la representación de las piezas de tal forma que
permita “rotar” y “empalmar” adecuadamente cada una de las piezas.
Figura 3. Piezas del rompecabezas a resolver
Nota: Se deben resolver 2 ejercicios de los 4 propuestos hasta aquí, para que pueda ser
válido como proyecto final del curso.
Otros proyectos pueden ser los siguientes:
1.- Programar el algoritmo A* en prolog, definido en la antología del curso página 10
2.- Programar el juego reversi/othello descrito en la antología del curso.