Tema 4: Fuentes y generadores

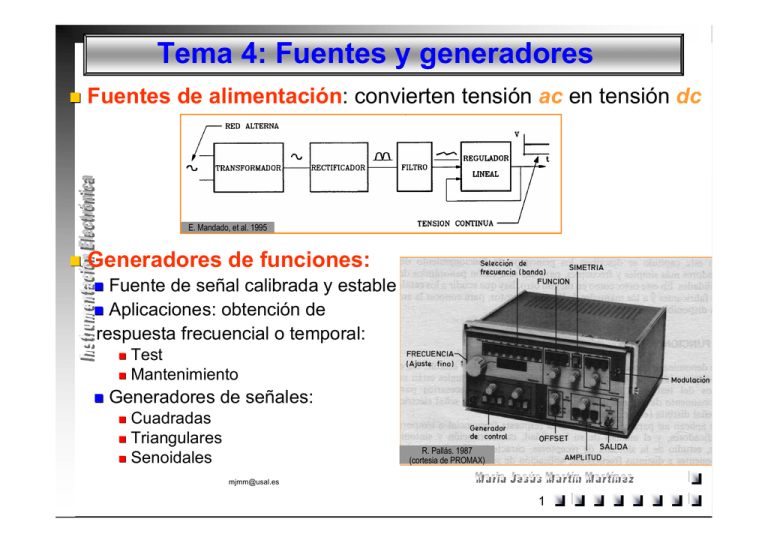
Tema 4: Fuentes y generadores

Fuentes de alimentación: convierten tensión ac en tensión dc
E. Mandado, et al. 1995

Generadores de funciones:
Fuente de señal calibrada y estable
 Aplicaciones: obtención de
respuesta frecuencial o temporal:

Test
 Mantenimiento


Generadores de señales:
Cuadradas
 Triangulares
 Senoidales

R. Pallás. 1987
(cortesia de PROMAX)
[email protected]
1
Tema 4: Fuentes de alimentación
Fuente de alimentación: circuito que convierte la tensión
alterna (red industrial) en una tensión prácticamente continua


Características y utilidad:
Casi todos los circuitos electrónicos necesitan una fuente de alimentación
continua.
 En sistemas portátiles (poca potencia)
batería

Bloques constituyentes: a grandes rasgos la fuente de alimentación
consta de tres bloques
fuente de alimentación regulada o
estabilizada

Transformador

Rectificador

Bloque de filtrado

Bloque estabilizador
Entrada
(alterna)
Regulador

Rectificador
Rectificador:
Transformador

Filtro
Salida
(continua
D. Pardo, et al. 1999
[email protected]
2
Tema 4: Rectificación (transformador)
Bloque de Rectificación: formador por un transformador y un
elemento rectificador

Transformador:
Adecua la tensión alterna a valores apropiados a la tensión de continua que
se desea obtener al final de la fuente de alimentación:


Aumenta o reduce la tensión de forma adecuada para nuestros propósitos
Primario
Secundario
Esta formado, básicamente por dos
arrollamientos:




Primario: nº de espiras n1
Secundario: nº de espiras n2
Dependiendo de n1, n2
La potencia es la misma, no
se amplifica ni se reduce como
en divisores de tensión)

[email protected]
Vo ≶ Vi
c.a.
V0
Vi
V=Vmáxsen
D. Pardo, et al. 1999
3
Tema 4: Rectificación

Rectificador:
Transforma en unidireccional la tensión bidireccional (o alterna)
 Es válido como rectificador cualquier elemento que :



R= ∞) al paso de la corriente en un sentido
Presente una resistencia muy pequeña ((ideal
R= 0) ) en el sentido opuesto
Presente una gran resistencia (ideal
Dispositivo electrónico que cumple estos requerimientos: diodo (unión p-n)

Característica del diodo

Si V
>0 
I  0 (R=0):
cortocircuito

Si V
Diodo
Característica del Diodo
ID
V
<0  I=0 (R=∞):
circuito abierto
[email protected]
V>0
ID
V<0
ID=0
VD
V
D. Pardo, et al. 1999
4
Tema 4: Rectificación

Rectificador:

Circuito rectificador más sencillo (denominado rectificador de media onda)
 Las formas de onda de tensiones en el circuito:
 La señal en la carga RL (V0) es unidireccional
pero resulta muy deficiente como tensión continua
para alimentar circuitos electrónicos
D. Pardo, et al. 1999
Diodo
V
Primario Secundario
Vmáx
Rectificador
t
de
media onda
c.a.
V
RL
V0
V0
Vmáx
t
V=Vmáxsen
[email protected]
5
Tema 4: Rectificación

Circuito rectificador de onda completa (transformador de toma intermedia)

Constituido por dos rectificadores de media onda conectados:

Un diodo conduce en un semiciclo

El otro diodo durante el otro semiciclo de la señal del secundario del transformador

La tensión de salida V0, puede observarse en la figura

La potencia entregada a la RL es mayor que en el de media onda

La tensión en RL es "más" continua
V
Rectificador
de
V
RL
V0
Vmáx
D. Pardo, et al. 1999
t
c.a.
onda completa
V0
V
Vmáx
t
V=Vmáxsent
[email protected]
6
Tema 4: Rectificación

Circuito rectificador de onda completa : PUENTE DE DIODOS
Transformador sin toma intermedia
 Necesita cuatro diodos

V
D. Pardo, et al. 1999
Vmáx
Rectificador
de
onda completa
t
c.a.
V
V0
V0
RL
Vmáx
t

Tensiones en la carga (RL) y en el secundario del transformador
D. Pardo, et al. 1999

Las corrientes en cada semiciclo:;



Vin > 0
V0= + Vin
Vin < 0
V0 = - Vin
V
V
V0
No perdemos potencia
[email protected]
V0
RL
RL
7
Tema 4: Rectificación

Rectificadores de Precisión: de media onda

Utilizan únicamente los diodos en circuitos que incluyen además AO
R
Rectificador de precisión:
AO + 2 diodos
de media onda
Vi
R
RL
R= 5.6 K
Tensiones en la entrada y en la
carga (RL)

RL= 5.6 K
D. Pardo, et al. 1999
V
Vmáx
D. Pardo, et al. 1999

t
V0
Las corrientes en cada semiciclo:
Vi >0
V0= 0 tensión
nula en el semiciclo positivo

(elimina problemas V)
V0
Vi <0
V0 = - Vin: en el
semiciclo negativo es un
inversor

Vmáx
t
[email protected]
8
Tema 4: Rectificación

Rectificadores de Precisión: de onda completa
Se basa en el anterior
utilizando una etapa inversora de modo que la
tensión realimenta y también realice la rectificación de la parte positiva de Vi

R
Rectificador de precisión:
AO + 2 diodos
de onda completa

Vi
R
R
Tensiones Vi y V0
V0
R/2
V
D. Pardo, et al. 1999
R
D. Pardo, et al. 1999
Vmáx
t

V0
Vmáx
[email protected]
Las corrientes en cada semiciclo:;

Vi > 0
V0= + Vin

Vi < 0
V0 = - Vin:
t
9
Tema 4: Filtrado

Filtrado:


Circuito cuya impedancia varía con la frecuencia de la señal que se le aplica.
Los filtros más sencillos están constituidos por un C o una L:
IL
IC
a.c. Rectificador
C
ZT 

1
1
jC 
RL
RL
VL
L
a.c. Rectificador
RL
VL
ZT  RL  jL
D. Pardo, et al. 1999
Para realizar una fuente de alimentación nos interesan los filtros pasa-baja
obtención de una señal de continua (Z baja para =0 )
 La asociación de L en serie con C en paralelo es también un filtro pasa-baja
[email protected]
10
Tema 4: Filtrado

Rectificación (media onda) + Filtrado:

CASO CONDENSADOR: Diodo actúa como un interruptor
 Si RL es elevada, entonces el condensador se carga y no se vuelve a descargar
Voltaje de continua (dc) perfecto

Como RL no es  entonces el condensador se carga en el semiciclo positivo y se
descarga poco a poco en el semiciclo negativo
D. Pardo, et al. 1999
Transformador
Rectificador
Filtro
V0,i
Punto de corte
i
i
c.a.
Punto umbral
RL
Vi
C
V0
V0
Vi
V=Vmáxsent
t1
 t2

[email protected]
11

Tema 4: Filtrado

Rectificación (onda
completa) + Filtrado:
(
La forma de onda es "más continua" que la del rectificador de media onda con
el mismo tipo de filtro.

Podemos observar la componente alterna linealizada de la tensión anterior,
sobre la que podría calcularse su valor eficaz para determinar el "rizado" de la
fuente de alimentación.

V
Vr
Vr/2
Vm
T1 T2
[email protected]
T/2
VCC
t
D. Pardo, et al. 1999
12
Tema 4: Regulación
Bloque de Regulación: una fuente de alimentación sólo con
rectificación y filtrado no es suficientemente buena

La tensión dc salida (V0) no es constante conforme varía la carga (RL)
 La tensión dc salida (V0) varía directamente con la entrada alterna (Vi)
 La tensión dc de salida varía con la temperatura

Para solventar estos tres inconvenientes y para reducir, además, la tensión
de rizado
bloque regulador en las fuentes de alimentación.


Puesto que V0 depende de :

La tensión no regulada

La corriente de salida

La temperatura
V0 
V0  SV Vi  R0 iL  ST T
SV 
Factor de estabilidad
[email protected]
 V0
V
V
Vi  0 iL  0 T
 Vi
 iL
T
V0
Vi
iL 0
T 0
Ro 
Resistencia de salida
V0
i L
Vi 0
T 0
ST 
V0
T Vi 0
Coeficiente de Tª
13
iL  0
Tema 4: Regulación

Bloque de Regulación:
Para obtener una regulación efectiva
menor posibles
SV, R0 y ST deben ser lo


Más constante será la tensión que suministra a la salida
Para cada circuito regulador que se a estudie a continuación deben determinarse
estos coeficientes


Ejemplos de reguladores:
D. Pardo, et al. 1999
R0
R0
RV
Vi
Vi
RL
iL
Regulador Serie
V0
RV
RL
Regulador paralelo
[email protected]
14
V0
Tema 4: Generadores de funciones

Generadores de funciones:
Fuentes de señal calibrada y estable
 Generadores de señales temporales:


Senoidales: sus parámetros son :
E. Mandado, et al. 1995
Frecuencia
 Amplitud de oscilación


Mandado, et al. 1995
Rectangulares: adoptan dos valores de tensión E.diferentes
Ondas cuadradas : t1= t2
 Impulsos de ondas rectangulares


E. Mandado, et al. 1995
Triangulares: pueden ser simétricas
Simétricas: pendiente ascendente = descendente
 No simétricas; pueden llegar a una rampa
de subida de 90º (diente de sierra)

[email protected]
15
Tema 4: Osciladores lineales
Osciladores lineales: circuito electrónico cuya función es producir una
onda de salida senoidal sin aplicar excitación de entrada:


Si conseguimos
Iguales en módulo
 Fases diferentes

v f  v s
via
Entrada
A
vs
vf

v0  Avf
Amplificador
 A 1
A
vf
 A 1
Salida
v0
Bloque de
realimentación
Podríamos eliminar vS y la señal
de salida se mantendría sin entrada

vf   v0
Amplificador
 A  180º
A(f), B(f)
frecuencia a la cuál se
produce la oscilación
aparece una señal sinusoidal
oscilación
[email protected]
D. Pardo, et al. 1999
Salida
v0
Bloque de
realimentación


Condición de
16
D. Pardo, et al. 1999
Tema 4: Osciladores lineales

Oscilador de puente de Wien: genera señal senoidal
Un circuito oscilante que utiliza un puente
equilibrado como red de realimentación

3
Z1
C
R1
R
Elemento activo
Ampl. Operacional
Ganancia muy elevada: GV
Resistencia de salida: R0 =0
Resistencia de entrada Ri = 
1
2

vi
R
G
R2
Z2
v0
C
4
D. Pardo, et al. 1999

Para encontrar la ganancia del lazo:


 G
Se rompe el lazo de realimentación en el punto 3
Se aplica una tensión externa V’0 entre terminales 3 y 4
v 0  Gv i
v
v
  G  0'  'i G
v0 v0
[email protected]
vi  v   v 
vi v   v 
  ' 
v0
v 0'
17
Tema 4: Osciladores lineales

Oscilador de puente de Wien: genera señal senoidal (continuación)

v0  G v   v 
v0  v 
Z  Z2
v0  v 1
Z2

3
C
R1  R2
R2
Z1 

Z2 
R1
Z1
1
R
R2
2
 RC  j
C
v0
R
Z2
R 1  j RC 
1   2R 2 C 2
vi
G
C
4
D. Pardo, et al. 1999
Condición
de oscilación: en la que se cumple que Z1 y Z2 tienen el mismo
desfase para una frecuencia 0=1/RC : fijada por R, C
Z1  R (1  j )
R
Z 2  1  j 
2
R1  R2 Z1  Z 2

R2
Z2
R1  2R2
[email protected]
18
Tema 4: Osciladores lineales
Oscilador de puente de Wien: genera señal senoidal (continuación II)
 Circuito a montar en el laboratorio
3

C



C= 10 nF
R1= 10 K
 R2= 5 K

Z1
Utilizar los siguientes valores
R= 5.6 K
R1
1
R
R2
2
0=1/RC
v0
R
Z2
C
0=2  f0
f0=2842 Hz
Oscilación
vi
G
4
D. Pardo, et al. 1999
R1  2R2
10 k
10 K
Utilizar un potenciómetro
o resistencia variable
[email protected]
19
Tema 4: Osciladores lineales

Oscilador de puente de Wien: genera señal senoidal (continuación III)
3
R2 muy baja: disminuye vC
V
VCC
t
R1
Z1
Realimentación
positiva:
NO OSCILA
1
R
vi
R2
2
v0
G
R
Z2
C
-VCC
4
T
D. Pardo, et al. 1999
R2 muy elevada: aumenta v-
V
V
VCC
t
-VCC
f0=861 Hz
Oscilación R2 =R1/2
T
Realimentación
negativa:
el circuito
oscila con
v0 en
saturación
VCC
t
-VCC
T
[email protected]
20
Tema 4: Osciladores lineales

Circuito generador de onda cuadrada

La realimentación positiva siempre
sigue a la salida:
v+= v0

I
R2
R1  R2
R
 En la salida el AO da los valores
de saturación:
+VCC, -VCC
Si v0=+VCC
v+=  VCC
La corriente I tiende a cargar el condensador C
v+= -  VCC
 Si v0=-VCC
La corriente I tiende a descargar el condensador C
vi
v0
G
R1
C

R2
D. Pardo, et al. 1999
Dependiendo de la carga y descarga del condensador C: la corriente I circula
en uno u otro sentido
se genera una onda cuadrada

[email protected]
21
Tema 4: Osciladores lineales

Circuito generador de onda cuadrada (continuación )
V0
I
VCC
R

t
1
R2

R1  R2 2
vi
-VCC
T
v0
G
R1
C
v+
R2
 VCC
t
En
- VCC
el laboratorio
D. Pardo, et al. 1999
R1=R2=10K
 R= 10 K
 C= 10 nF

 VCC
vt
- VCC
[email protected]

El periodo de la oscilación:

R 
T  2 RC ln1  2 2 
R1 

f0=4500 Hz
22

Agradecimientos


Daniel Pardo Collantes. Departamento de Física Aplicada.
Universidad de Salamanca.
Figuras cortesía de:




PROMAX. www.promax.es.
R. Pallás, Instrumentación Electrónica. Marcombo, 1987.
E. Mandado, P. Mariño y A. Lago, Instrumentación
Electrónica. Marcombo. 1995.
Pardo Collantes, Daniel; Bailón Vega, Luís A., Universidad
de Valladolid. Secretariado de Publicaciones e Intercambio
Editorial.1999.
[email protected]
23