Objetivos 1. Variable Aleatoria y Función de Probabilidad

M. Iniesta
Grado en Ciencia y Tecnología de los Alimentos
Universidad de Murcia
Tema 4:
Variables aleatorias discretas
Objetivos
Dominar el uso de las funciones asociadas a una variable aleatoria discreta para
calcular probabilidades.
Conocer el signicado y saber calcular la esperanza y la varianza de una variable
aleatoria discreta.
Reconocer y aplicar modelos de probabilidad discretos
1.
Variable Aleatoria y Función de Probabilidad
Lo que pretendemos en este tema es transformar el problema de la asignación de
probabilidades a otro consistente en el empleo de ciertas funciones reales de variable
real, de forma que la probabilidad de cierto suceso aleatorio vendrá dada por el cálculo
de ciertos valores de dichas funciones.
1.1. Denición de Variable aleatoria
Sea Ω el espacio muestral asociado a un fenómeno aleatorio. Una variable aleatoria
es una función
X:Ω→R
que asocia a cada suceso elemental un número real. El conjunto X(Ω) = X se le llamará
espacio muestral de la variable aleatoria X y es el conjunto de todos los valores
posibles de X .
Diremos que una variable aleatoria es discreta si su espacio muestral es un conjunto
discreto, es decir, un conjunto nito o bien un conjunto innito pero numerable. Si el
espacio muestral de la variable es innito no numerable, como el conjunto de puntos de
un intervalo real, diremos que la variable aleatoria es continua. En este tema trataremos
con variables aleatorias discretas.
Ejemplo 1.1 Si lanzamos una moneda al aire dos veces y
obtenidas X transforma
X = {0, 1, 2}.
el espacio muestral original
X es el número de caras
Ω = {(c, c), (x, c), (c, x), (x, x)} en
1.2. Función de Probabilidad
La función puntual de probabilidad va a asignar probabilidad a cada punto del espacio
muestral de X .
Tema 4
Página: 1
M. Iniesta
Grado en Ciencia y Tecnología de los Alimentos
Universidad de Murcia
Si X es una variable aleatoria discreta, la Función
simplemente la Función de Probabilidad es la función
Puntual de Probabilidad
o
p : R → [0, 1]
que asigna probabilidades a cada uno de los puntos muestrales de X . Es decir,
p(x) =
P (X = x), si x ∈ X ;
0,
si x ∈
/ X.
es decir
De la denición se derivan las siguientes propiedades de la función de probabilidad:
1. Se dene la Función de Distribución de la variable X como F (x) = y∈X ,y≤x p(y) =
F (x). La función F (x), en este caso, acumula la probabilidad asociada al punto
muestral x a la de los puntos muestrales menores que x.
P
2.
P
x∈X
p(x) = 1
3. Si I ⊆ R, P (X ∈ I) =
Ejemplo 1.2 Si
probabilidad es
P
x∈I,x∈X
p(x)
X =número de caras al tirar dos veces una moneda,

 1/4, si x = {0, 2};
1/2, si x = 1;
p(x) =

0,
si x ∈
/ {0, 1, 2}.
su función de
y su función de distribución es

0



1/4,
F (x) =
3/4,



1,
si
si
si
si
x < 0;
x ∈ [0, 1);
x ∈ [1, 2);
x ≥ 2.
1.3. Actividades
Estudiar si las funciones siguientes pueden ser funciones puntuales de probabilidad
1. p(x) =
1
si x = 0, 1, 2, 3, 4 y p(x) = 0 en el resto
5
2. p(x) = k si x = −10, −9, ..., 9, 10 y p(x) = 0 en el resto
3. p(x) =
2.
2x + 1
si x = 1, 2, 3, 4 y p(x) = 0 en el resto
24
Esperanza y Varianza de una variable aleatoria discreta
Con estos parámetros, que denimos a continuación, pretendemos describir una variable aleatoria respecto a sus características de centralización y dispersión.
Tema 4
Página: 2
M. Iniesta
Grado en Ciencia y Tecnología de los Alimentos
Universidad de Murcia
2.1. Esperanza Matemática o Media Teórica
La Esperanza o Media Teórica de una v.a. E(X) indica un valor teórico al que
tendería el valor medio de n realizaciones de X , cuando n tiende a innito. Para aclarar
esto supongamos que X es nuestra ganancia cuando jugamos a un juego de lotería en
el que podemos ganar un millón de euros con cierta probabilidad o perder lo invertido
en el billete. En una realización concreta ganaremos o perderemos y la esperanza de X
sería el valor al que tendería el valor medio de mi ganancia cuando juego un número
grande de veces.
Se dene mediante la siguiente expresión:
E(X) =
X
xp(x)
x∈X
Ejemplo 2.1 Supongamos que en un juego ganamos 10 euros si al tirar un dado sacamos
un cinco o un seis, ganamos 5 si sale un 2 o un 3 o un 4 y perdemos 25 si sale un 1. Si
llamamos
X
a la ganancia obtenida en una jugada, la función de probabilidad de
 2
,


 63
,
6
p(x) =
1
,


 6
0,
cuya esperanza vale:
si
si
si
si
X
es
x = 10;
x = 5;
x = −25;
x∈
/ {10, 5, −25}.
3
1
10
2
E(X) = 10 + 5 − 25 =
6
6
6
6
que sería el valor medio de nuestras ganancias a largo plazo (en un gran número de
jugadas).
Ejemplo 2.2 La esperanza de la variable del ejemplo (1.1) vale
1
1
1
E(X) = 0. + 1. + 2. = 1
4
2
4
esto signica que en un gran número de experiencias, el valor medio del número de caras
tendería a 1.
2.2. Varianza y Desviación Típica
La varianza de una variable aleatoria X , que representaremos por V (X), y la Desviación Típica, D(X), indicarán el grado de dispersión de los valores de la variable respecto
a la esperanza matemática.
La Desviación Típica será la raíz cuadrada positiva de la
p
varianza, D(X) = V (X) y tiene la ventaja que se expresa en la misma unidad que la
propia variable. Variables con desviación típica pequeña indicará que hay alta probabilidad de observar valores próximos a la esperanza matemática o media teórica E(X). Si
denotamos E(X) mediante µ y V (X) mediante σ 2 Denimos
V (X) = σ 2 = E((X − µ)2 ) = E(X 2 ) − µ2
y podemos calcularla mediante la siguiente expresión:
V (X) = σ 2 =
X
x∈X
Tema 4
x2 p(x) − µ2 =
X
x∈X
x2 p(x) − (
X
xp(x))2
x∈X
Página: 3
M. Iniesta
Grado en Ciencia y Tecnología de los Alimentos
Universidad de Murcia
Ejemplo 2.3 La varianza de la variable del ejemplo (1.1) es
1
1
1
1
σ 2 = 02 + 12 + 22 − 12 =
4
2
4
2
y su desviación típica es
1
D(X) = σ = √
2
2.3. Actividades
Calcular la esperanza y la varianza en los casos en donde sea posible de las actividades
de la sección 1.3.
3.
Modelos de probabilidad discretos
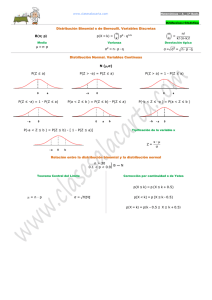
3.1. El modelo de Bernoulli
Consideremos un experimento con únicamente dos resultados posibles, o puede suceder A (que llamaremos éxito ) o bien A y supongamos que la probabilidad de Éxito es
conocida, es decir, P (A) = p (con 0 ≤ p ≤ 1 ).
Cuando realizamos un experimento en las condiciones anteriores diremos que hemos
realizado una Prueba de Bernoulli.
Si llamamos
X=número de éxitos obtenidos en una prueba de Bernoulli
su espacio muestral es X = {0, 1} y la función puntual de probabilidad de X tiene la
siguiente expresión

si X = 1;
 p,
q = (1 − p), si X = 0;
p(x) = P (X = x) =

0,
en otro caso.
o lo que es igual
p(x) = P (X = x) =
px (1 − p)1−x , si x ∈ X = {0, 1};
0,
en otro caso.
Podemos, para este modelo, fácilmente calcular su esperanza y su varianza: que son
E(X) = 1p + 0(1 − p) = p
V (V ) = 12 p + 02 (1 − p) − p2 = p(1 − p)
Si la variable X tiene una distribución de probabilidad como la del modelo de Bernoulli con P (A) = p, lo indicaremos poniendo
X ∼ B(p)
Tema 4
Página: 4
M. Iniesta
Grado en Ciencia y Tecnología de los Alimentos
Universidad de Murcia
3.2. Modelo Binomial
Imaginemos un experimento como el anterior, con dos resultados posibles A y A y
P (A) = p conocido, pero que lo repetimos n veces en idénticas condiciones. Sea ahora
X=número de éxitos en n pruebas de Bernoulli idénticas e independientes
El espacio muestral de la variable es X = {0, 1, ...., n} y la función puntual de probabilidad es:
n x
p (1 − p)n−x , si x ∈ X = {0, 1, ..., n};
x
p(x) =
0,
si x ∈
/ X.
En este caso la esperanza y la varianza valen:
E(X) = np
V (X) = np(1 − p)
Si la variable X tiene una distribución de probabilidad como la del modelo Binomial
de parámetros n =número de pruebas y P (A) = p, lo indicaremos poniendo
X ∼ B(n, p)
3.2.1.
Actividades
1. Aporta cinco situaciones experimentales en donde la v.a. X siga una distribución
Binomial.
2. Demuestra que la función puntual de probabilidad anteriormente denida cumple
los requisitos necesarios.
3.3. Modelo Hipergeométrico
Supongamos una urna con N bolas de dos tipos, por ejemplo N1 blancas y N2 =
N − N1 negras, y supongamos que denimos la v.a.
X =número
miento.
de bolas blancas obtenidas en una muestra de tamaño n con reemplaza-
Puesto que las distintas extracciones son independientes y la probabilidad de
obtener bola blanca es igual en cada extracción (P (A) = NN1 ) la variable anterior sigue
una distribución Binomial, es decir X ∼ B(n, NN1 ).
Pero vamos a suponer ahora que de dicha población se extraen n bolas sin reemplazamiento. El modelo ya no es binomial puesto que las distintas extracciones ni son
independientes ni tienen la misma probabilidad de éxito.
Si la población consta de N objetos, con N1 objetos de la clase A y N2 objetos de la
clase A (N1 + N2 = N ), denimos ahora la variable
X=número de objetos de la clase A en una muestra de tamaño n extraída sin reemplazamiento
Tema 4
Página: 5
M. Iniesta
Grado en Ciencia y Tecnología de los Alimentos
Universidad de Murcia
el espacio muestral es X = {máx{0, n−(N −N1 )}, ....., mı́n{N1 , n}} y su función puntual
de probabilidad es
(
p(x) =
−N1
)
(Nx1 )(Nn−x
, si máx{0, n − (N − N1 )} ≤ x ≤ mı́n{N1 , n};
N
(n)
0,
en otro caso.
En este caso la esperanza y la varianza valen:
E(X) = n NN1
V (X) = n NN1 (1 −
N1 N −n
)
N N −1
Si la variable X tiene una distribución de probabilidad como la del modelo hipergeométrico lo indicaremos poniendo
X ∼ H(N, N1 , n)
donde N es tamaño de la población, n es el tamaño de la muestra y N1 es el número de
objetos de la clase A en la población.
Además es posible demostrar que si N es muy grande y n es pequeño frente a N , las
probabilidades hipergeométricas valen aproximadamente las probabilidades binomiales;
haciendo p = NN1 ,
H(N, N1 , n) → B(n,
es decir
lı́m
N →∞
N1
x
N1
) si N → ∞,
N
N −N1
n−x
N
n
p=
N1
N
n x
=
p (1 − p)n−x
x
Lo anterior supone que cuando se dan esas circunstancias en problemas de extracción
de muestras (N grande y n pequeño), podemos suponer reemplazamiento porque los
resultados van a ser muy parecidos y es más cómodo trabajar en este caso.
3.3.1.
Actividades
1. Dene cinco situaciones experimentales que se asocien al modelo hipergeométrico,
expresando en cada caso cuál es el espacio muestral.
2. Si una urna contiene 95 bolas blancas y 5 negras y elegimos al azar 3 sin reemplazamiento, calcula la probabilidad de obtener 2 bolas blancas y 1 negra.
3. Calcula una aproximación de la probabilidad anterior, mediante la aproximación
de la distribución hipergeométrica a la distribución binomial.
Tema 4
Página: 6
M. Iniesta
Grado en Ciencia y Tecnología de los Alimentos
Universidad de Murcia
3.4. Modelo de Poisson
Supongamos que conocemos el número medio de veces que ocurre el suceso A en una
unidad de soporte continuo (tiempo, espacio, volumen, longitud, supercie,....) y que
vamos a denotar mediante λ. Decimos que la variable
X =número
de veces que ocurre A en un intervalo unidad
cuyo espacio muestral es X = {0, 1, 2, ...}, sigue una distribución de Poisson (también
llamada Ley de los Sucesos Raros) de parámetro λ si su función de probabilidad está
dada por:
−λ λx
e x! , si x ∈ X = {0, 1, 2, ....};
p(x) =
0,
en otro caso.
En este caso:
E(X) = λ
V (X) = λ
Si X es una variable cuya distribución de probabilidad es como la del modelo de Poisson,
lo indicaremos poniendo
X ∼ P(λ)
donde λ = E(X) es el número medio de veces que ocurre A en un intervalo unidad.
Además las probabilidades Binomiales cuando n es grande y p es pequeño se aproximan a las probabilidades de Poisson, haciendo λ = np. Es decir,
n x
λx
p (1 − p)n−x → e−λ ,
x!
x
si n → ∞,
λ = np
Lo anterior signica que podemos aproximar probabilidades binomiales mediante
probabilidades de Poisson cuando n sea sucientemente grande y p pequeño.
Ejemplo 3.1 En un núcleo urbano de
n = 100000
personas la probabilidad de infección
p = 0.00002, el número X =Número de infectados sigue
X ∼ B(100000, 0.00002) que podemos aproximar a un modelo de
parámetro λ = np = 2. La probabilidad exacta, según el modelo Binomial, de
de cada una de ellas es
un modelo Binomial
Poisson de
que en un determinado momento haya más de un infectado es
P (X > 1) = 1 − P (X = 0) − P (X = 1) = 1 − 0.1353326 − 0.2706706 = 0.5939969
Mientras que aproximando la misma probabilidad por el modelo de Poisson se obtiene
P (X > 1) = 1 − P (X = 0) − P (X = 1) = 1 − 0.1353353 − 0.2706706 = 0.5939942
(Todas las probabilidades anteriores se calcularon mediante R)
Tema 4
Página: 7
M. Iniesta
Grado en Ciencia y Tecnología de los Alimentos
3.4.1.
Universidad de Murcia
Actividades
1. Denir cinco situaciones experimentales que se ajusten a un modelo de Poisson.
Establecer el parámetro λ en cada caso.
2. Denir cinco situaciones experimentales que se ajusten a un modelo de Binomial
pero con aproximación razonablemente buena al modelo de Poisson. Establecer en
cada caso los correspondientes parámetros.
4.
Bibliografía
1. Tema 2, sección 2 del texto Estadística para Ciencias Agropecuarias. Autor: Di
Riezo, J. A.
2. Tema 2 del texto Probabilidad y Estadística
Delgado de la Torre. Editorial Delta.
para Ciencias e Ingenierías.
Rosario
3. Tema 2, secciones 2.3 y 2.4 y Tema 4, secciones 4.1, 4.2, 4.3 y 4.4 del texto Estadística para ingenieros y cientícos. William Navidi. Editorial McGraw-Hill.
Tema 4
Página: 8