Esfuerzo de tensión y compresión

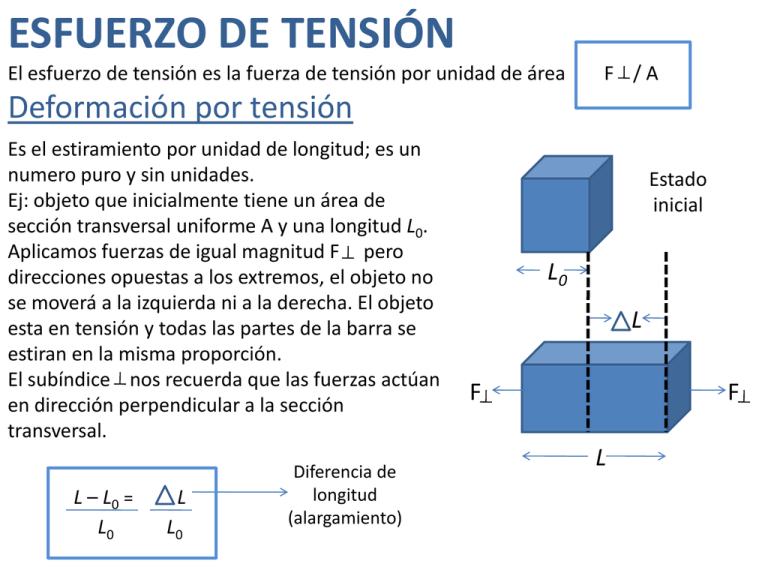
ESFUERZO DE TENSIÓN
El esfuerzo de tensión es la fuerza de tensión por unidad de área
F /A
Deformación por tensión
Es el estiramiento por unidad de longitud; es un
numero puro y sin unidades.
Ej: objeto que inicialmente tiene un área de
sección transversal uniforme A y una longitud L0.
Aplicamos fuerzas de igual magnitud F pero
direcciones opuestas a los extremos, el objeto no
se moverá a la izquierda ni a la derecha. El objeto
esta en tensión y todas las partes de la barra se
estiran en la misma proporción.
El subíndice nos recuerda que las fuerzas actúan
en dirección perpendicular a la sección
transversal.
L – L0 =
L0
L
L0
Diferencia de
longitud
(alargamiento)
Estado
inicial
L0
L
F
F
L
Modulo de Young
Se observa experimentalmente que si el esfuerzo de tensión es lo bastante pequeño, el esfuerzo
y la deformación son proporcionales. Se le denomina módulo de Young al módulo de elasticidad
correspondiente.
Y =
Esfuerzo de tensión
= F / A = F . Lo
Deformación por tensión
L / LO
A. L
Un material con un valor grande de Y no se estira mucho; se requiere un esfuerzo grande para
una deformación dada.
Módulo de elasticidad aproximados
Material
Módulo de Young Y (Pa)
Módulo de Volumen B (Pa) Módulo de corte S (Pa)
Aluminio
7.0 x 1010
7.5 x 1010
2.5 x 1010
Latón
9.0 x 1010
6.0 x 1010
3.5 x 1010
Cobre
11 x 1010
14 x 1010
4.4 x 1010
Vidrio óptico
6.0 x 1010
5.0 x 1010
2.5 x 1010
Hierro
21 x 1010
16 x 1010
7.7 x 1010
Plomo
1.6 x 1010
4.1 x 1010
0.6 x 1010
Níquel
21 x 1010
17 x 1010
7.8 x 1010
Acero
20 x 1010
16 x 1010
7.5 x 1010
La ley de Hooke y la ecuación del modulo de Young
son válidas también para la compresión si el
esfuerzo no es muy grande. El módulo de Young de
muchos materiales tiene el mismo valor para
esfuerzos de tensión y compresión, materiales
como hormigón y concreto son una excepción.
Estado
inicial
L0
L
Deformación por compresión
Si las fuerzas en los extremos de una barra empujan en
lugar de tirar, la barra esta en compresión y el esfuerzo
es un esfuerzo de compresión.
Se define del mismo modo que la deformación por
tensión pero,
L tiene la dirección opuesta.
F
F
L
En muchas situaciones, los cuerpos experimentan
esfuerzos de tensión y compresión al mismo tiempo. Ej:
una viga horizontal apoyada en sus extremos se pandea
por su propio peso. La parte superior de la viga esta en
compresión y la inferior en tensión.
Compresión
Tensión
Ejercicio
Un cable de acero de 2.0m de longitud tiene un área transversal de 0.30 cm2 .
El cable se cuelga por un extremo de una estructura de soporte y después un torno de
550kg se cuelga del extremo inferior del cable.
Determine el esfuerzo, la deformación y el alargamiento.
Esfuerzo = F
Deformación =
Alargamiento =
/A
L
L0
Esfuerzo
Y ( en el acero: 20 x 1010 Pa)
L = Deformación . L0
= (550kg) (9.8 m/s2) = 1.8 x 108 Pa
Esfuerzo = F
A
Deformación =
Alargamiento =
L0
3.0 x 10-5
L = Esfuerzo = 1.8 x 108 Pa = 9.0 x 10-4
Y
20 x 1010 Pa
L = Deformación . L0 = (9.0 x 10-4 ) (2.0m) = 0.0018m = 1.8 mm