SUMA EN BCD

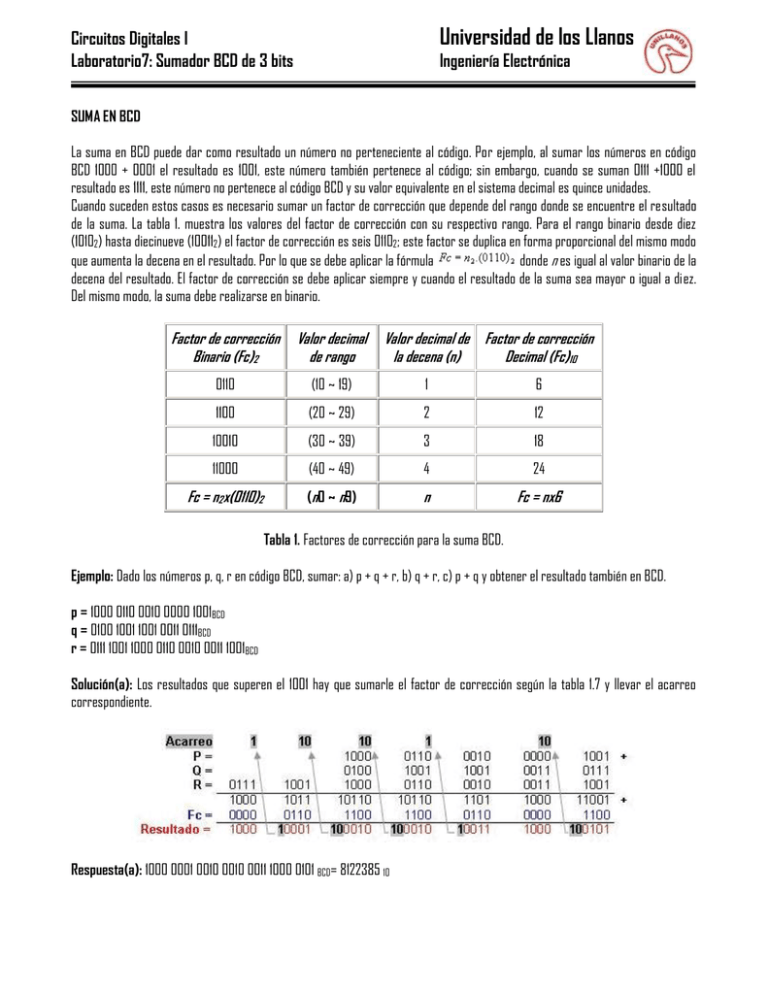
Universidad de los Llanos
Circuitos Digitales I
Laboratorio7: Sumador BCD de 3 bits
Ingeniería Electrónica
SUMA EN BCD
La suma en BCD puede dar como resultado un número no perteneciente al código. Por ejemplo, al sumar los números en código
BCD 1000 + 0001 el resultado es 1001, este número también pertenece al código; sin embargo, cuando se suman 0111 +1000 el
resultado es 1111, este número no pertenece al código BCD y su valor equivalente en el sistema decimal es quince unidades.
Cuando suceden estos casos es necesario sumar un factor de corrección que depende del rango donde se encuentre el resultado
de la suma. La tabla 1. muestra los valores del factor de corrección con su respectivo rango. Para el rango binario desde diez
(10102) hasta diecinueve (100112) el factor de corrección es seis 01102; este factor se duplica en forma proporcional del mismo modo
que aumenta la decena en el resultado. Por lo que se debe aplicar la fórmula
donde n es igual al valor binario de la
decena del resultado. El factor de corrección se debe aplicar siempre y cuando el resultado de la suma sea mayor o igual a diez.
Del mismo modo, la suma debe realizarse en binario.
Factor de corrección
Binario (Fc)2
Valor decimal
de rango
Valor decimal de Factor de corrección
la decena (n)
Decimal (Fc)10
0110
(10 ~ 19)
1
6
1100
(20 ~ 29)
2
12
10010
(30 ~ 39)
3
18
11000
(40 ~ 49)
4
24
Fc = n2 x(0110)2
(n0 ~ n9)
n
Fc = nx6
Tabla 1. Factores de corrección para la suma BCD.
Ejemplo: Dado los números p, q, r en código BCD, sumar: a) p + q + r, b) q + r, c) p + q y obtener el resultado también en BCD.
p = 1000 0110 0010 0000 1001BCD
q = 0100 1001 1001 0011 0111BCD
r = 0111 1001 1000 0110 0010 0011 1001BCD
Solución(a): Los resultados que superen el 1001 hay que sumarle el factor de corrección según la tabla 1.7 y llevar el acarreo
correspondiente.
Respuesta(a): 1000 0001 0010 0010 0011 1000 0101 BCD= 8122385 10
Circuitos Digitales I
Laboratorio7: Sumador BCD de 3 bits
Universidad de los Llanos
Ingeniería Electrónica
MATERIALES







C.I’s 74LS83 o 74LS283 y 74LS47
Dipsiwtch.
Resistencias
Fuente.
Multimetro.
3 displays 7 segmentos
Protoboard y cable.
PROCEDIMIENTO
1.
Se propone diseñar un circuito para la suma de dos números binarios codificados en BCD (X y Y) de 3 bits y su posterior
visualización. sobre 3 displays de siete segmentos. Las entradas para el numero X serán los bits X11X10X9X8 X7X6X5X4 X3X2X1X0 y
para el numero Y serán los bits Y11Y10Y9Y8 Y7Y6Y5Y4 Y3Y2Y1Y0 y para la salida S serán los bits S11SS0S9S8 S7S6S5S4 S3S2S1S0. (por
ejemplo para sumar 182 + 044 = 226 la entradas para X serán 0001 1000 0010 y para Y serán 0000 0100 0100, obteniendo en
la salida S: 0010 0010 0110). Para visualizar el resultado se utilizarán 3 displays 7 segmentos. Activar los segmentos
adecuados en función del número BCD que se quiera representar es una simple función combinacional que ya esta
implementada con el circuito 7447.
2. solucione los literales b) y c) del ejemplo planteado anteriormente indicando el resultado en BCD y en base 10.
3. Investigue acerca de la conversión decimal fraccionario – BCD y la conversión BCD fraccionario – Decimal.