Distribuciones normales.

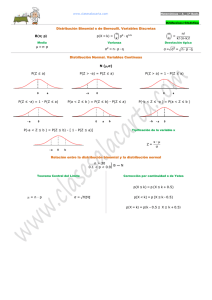
Distribuciones normales.
Cálculo Numérico y Estadística. Grado en Química. U. de Alcalá. Curso 2014-2015.
F. San Segundo.
Función de densidad de la familia de distribuciones normales.
Empezamos recordando un hallazgo fundamental que hemos hecho al nal de la primera parte
de este capítulo. Si tenemos una binomial B(n, p) con n grande (n > 30) y p moderado, de
manera que
μ = n ⋅ p , σ = √−
n−⋅−p−−
⋅−
q,
entonces la curva que aproxima a la binomial es la
grá ca de la función normal:
x−μ
1
− 12 ( σ )
fμ,σ (x) =
−− e
σ√2π
2
Se trata de una familia de curvas, que cambian con los valores de μ y σ:
·
μ indica la posición del máximo de la campana.
·
σ controla la anchura de la campana.
2/15
La distribución normal en GeoGebra.
Una de las mejores maneras de explorar esta familia de curvas normales es usando GeoGebra.
Concretamente, con estos comandos:
mu = Deslizador[-5, 5, 0.05, 0, 200]
sigma = Deslizador[0, 2, 0.05, 0, 200]
sigma = 1
Normal[mu, sigma, x]
RazónEjes[20,3]
Obtendrás un resultado como este:
Puedes descargar un chero con estos comandos en este enlace Más adelante veremos otras
formas de trabajar con las curvas normales en Geogebra y R (ver Tutorial05).
3/15
Regla 68 - 95 - 99.
Esta propiedad, que se cumple para todas las curvas normales señala la conexión que existe
entre todas las funciones de esa familia:
Si X es una variable normal de tipo N(μ, σ) entonces se cumplen estas
aproximaciones (las probabilidades con tres cifras signi cativas):
⎧ P (μ − σ < X < μ + σ) ≈ 0.683,
⎨ P (μ − 2σ < X < μ + 2σ) ≈ 0.955
⎩
P (μ − 3σ < X < μ + 3σ) ≈ 0.997
En resumen, si tenemos una colección de datos con distribución normal, es bastante raro
encontrar un valor que se diferencie de la media en más de una desviación típica (ocurre
menos del 5% de las veces) y es más raro aún encontrar un valor a más de tres desviaciones
típicas de la media (sucede con menos del 1% de los valores).
4/15
Tipi cación.
La razón última por la que ocurre lo anterior es porque todas las variables normales están
relacionadas mediante un cambio de escala. Concretamente:
Si X
∼ N(μ, σ), entonces la variable que se obtiene mediante:
X−μ
Z=
σ
es una variable normal estándar N(0, 1) , que en Estadística siempre
llamamos Z .
Este cambio de escala para obtener el valor de Z a partir del de X se llama tipi cación.
· La regla 68 - 95 - 99, combinada con la tipi cación, nos dice que si al tipi car un valor de una
distribución normal obtenemos un resultado mayor que
considerarse raro.
2 en valor absoluto, el valor puede
· Gracias a ideas como estas y a la omnipresencia de distribuciones normales en la
naturaleza, podemos considerar a Z como una especie de escala universal probabilidad (o de
rareza).
5/15
Ejemplo.
Los resultados de una Marathon dependen de otros factores, aparte del rendimiento de los
atletas: el per l de la prueba, el viento, la humedad del aire, etc. Si quieres comparar los
resultados de dos atletas en dos pruebas, una forma de hacerlo es tipi cando. Por ejemplo,
supongamos que en la Marathon 1 los corredores obtuvieron un tiempo medio de
μ1 = 4.68
horas con una desviación típica de σ1 = 1.01 horas, mientras que en la Marathon 2 el tiempo
medio fue μ2 = 4.43 con una desviación típica σ2 = 1.12 . Dos amigos participaron cada
uno en una de estas dos pruebas y quieren saber quién de ellos lo hizo mejor. El que participo
en la primera prueba obtuvo un tiempo X1
tiempo de X2 = 3.75 .
= 3.91 , mientras que el de la segunda obtuvo un
Suponiendo que los tiempos de los corredores en cada Marathon son
X1 ∼ N(4.68, 1.01)
X2 ∼ N(4.43, 1.12)
y tipi cando,
3.91 − 4.68
≈ −0.762,
1.01
3.75 − 4.43
≈ −0.607,
1.12
Así que, teniendo en cuenta las diferencias entre ambas pruebas, en realidad hizo mejor
carrera el primero de ellos, a pesar de que su tiempo total fue mayor.
6/15
Suma de variables normales independientes.
Ya sabemos que si X1 y X2 son dos variables aleatorias independientes, entonces
μX1 +X2 = μX1 + μX2
y también
2
2 + σ2
σX
=
σ
+
X
X
X2
1
2
1
Pero en el caso de las variables normales, la forma también se conserva: la suma, además, es
también una normal.
Si X1 ∼ N(μ1 , σ1 ) y X2 ∼ N(μ2 , σ2 ), son variables normales
independientes, su suma es de nuevo una variable normal de tipo:
−−−−−−
N(μ1 + μ2 , √σ12 + σ22 ).
Este resultado se generaliza a la suma de
resultado una normal de tipo
k variables normales independientes, que dan como
−−
−−−−−−−−−
2
N(μ1 + ⋯ + μk , √σ1 + ⋯ + σk2 ).
7/15
Problema directo de probabilidad en las distribuciones normales.
La tipi cación hace especialmente importantes los problemas relacionados con la distribución
Z ∼ N(0, 1) . Al trabajar con Z nos vamos a encontrar a menudo con dos tipos de preguntas
concretas. En los que vamos a llamar problemas directos de probabilidad los datos que
tenemos son intervalos de valores de Z , y lo que se quiere averiguar es la probabilidad de que
Z
pertenezca a uno de esos intervalos. Por ejemplo, dados los valores
a, b,
calcular la
probabilidad
P (a < Z < b)
También pueden ser problemas con intervalos no acotados como P (Z
> 3) =??
8/15
Problema inverso de probabilidad en las distribuciones normales.
En cambio, en un problema inverso de probabilidad el dato es la probabilidad, y lo que
queremos averiguar es el valor de Z que de ne un cierto intervalo cuya probabilidad coincide
con la que nos han dado.
Se entiende mejor con un ejemplo. Dada una probabilidad
el que se cumple P (Z
> a) = 0.25? En una
P = 0.25 , ¿cuál es el valor a para
gura:
Problemas directos e inversos en distribuciones normales cualesquiera.
Aunque los hemos descrito en el caso de Z , estos dos tipos de problemas se extienden de
forma natural a otras distribuciones normales. Y como veremos más adelante, también a otras
distribuciones no normales.
9/15
Las distribuciones normales en R. Funciones pnorm, qnorm.
Es importante recordar que R usa siempre por defecto la cola izquierda de las distribuciones
y que, si no se indican media y varianza, R asume que estamos usando Z ∼ N(0, 1) .
· pnorm sirve para resolver problemas directos de probabilidad. Por ejemplo, si
X ∼ N(12, 0.6) y queremos resolver el problema P (X < 13) =?? usaríamos:
pnorm(13, mean = 12, sd = 0.6)
## [1] 0.9522096
X ∼ N(12, 0.6) y queremos
averiguar cuál es el valor k para el que se cumple P (X ≤ K) = 0.9522096 usaríamos
· qnorm sirve para los problemas inversos de probabilidad. Si
qnorm(0.9522096, mean = 12, sd = 0.6)
## [1] 13
Más detalles en la Sección 5 del Tutorial 5.
10/15
Función rnorm.
La función rnorm genera valores aleatorios de una distribución normal y por lo tanto es
extremadamente útil para hacer simulaciones y experimentos.
Por ejemplo, podemos generar
1000
valores de una normal
N(23, 4)
y dibujar su
histograma con este comando:
hist(rnorm(1000, mean = 23, sd = 4), breaks=15, col="orange")
Hay también una función dnorm que sirve para dibujar curvas normales y que vamos a usar
poco o nada en este curso.
11/15
Problemas directos e inversos con normales en GeoGebra.
En GeoGebra disponemos de una forma muy visual de afrontar los dos tipos de problemas,
usando la Calculadora de Probabilidades
Además, disponemos de los comandos Normal y NormalInversa para usar directamente en
la Línea de Entrada o en la Vista Simbólica. Para más detalles nos remitimos a la Sección 4.1 del
Tutorial04.
12/15
Advertencia: no todas las distribuciones son normales.
Hemos visto que las distribuciones binomiales con n grande y p moderado se aproximan
mediante distribuciones normales. Este hecho, junto con la composición celular de muchos
seres vivos y la composición atómica de la materia, permite entender porque muchos
fenómenos naturales parecen comportarse, a escala macroscópica, como si siguieran una
distribución normal.
No obstante, también hay muchos otros fenómenos naturales, asimismo a escala
macroscópica, que no se pueden describir adecuadamente mediante las distribuciones
normales. Debe tenerse siempre en cuenta que las distribuciones normales son muy
simétricas. Y hay muchos casos en los que nos encontraremos con datos que son
inherentemente asimétricos, con sesgos muy de nidos, como en la gura de abajo. Existen
otras distribuciones estadísticas adecuadas para estas situaciones (más detalles en el libro).
13/15
Teorema Central del Límite: la normal para aproximar la binomial.
Recuerda que hemos llegado a las distribuciones normales tratando de aproximar los valores
de binomiales con n grande y p moderado.
Sea X
∼ B(n, p) y sea
μ = n ⋅ p, σ = √−
n−⋅−p−−
⋅−
q
Entonces, siempre que se cumpla
n ⋅ p > 5, n ⋅ q > 5
(si no, la aproximación no es muy
buena),
P (k1 ≤ X ≤ k2 ),
P (k1 − 0.5 ≤ Y ≤ k2 + 0.5) .
· para calcular
P (X = k), la
P (k − 0.5 ≤ Y ≤ k + 0.5) .
· Para
calcular
la aproximación por la normal que usamos es
aproximación
por
la
normal
que
usamos
es
· Para calcular P (X
≤ k), la aproximación por la normal que usamos es P (Y ≤ k + 0.5).
Del mismo modo, para P (X ≥ k), la aproximación por la normal que usamos es
P (Y ≥ k − 0.5)
Puedes ver en el libro (Sección 5.6.2) por que hacemos esos ajustes de 0.5 unidades.
14/15
Ejemplo.
Dada una binomial X
∼ B(320, 0.25) , para calcular la probabilidad
P (70 ≤ X ≤ 90)
−−−−−−−−−−−−−
−−
usamos la normal Y ∼ N(320 ⋅ 0.25, √320 ⋅ 0.25 ⋅ 0.75 ) = N(80, √60 )
y calculamos
P (70 − 0.5 ≤ Y ≤ 90 + 0.5) = P (69.5 ≤ Y ≤ 90.5)
En R esto se obtiene con
pnorm(90.5, mean = 80, sd = sqrt(60)) - pnorm(69.5, mean = 80, sd = sqrt(60))
## [1] 0.8247558
El cálculo directo con la binomial es:
sum(dbinom(70:90, size = 320, prob = 0.25))
## [1] 0.8250121
Así que hemos obtenido cuatro cifras decimales signi cativas, que no está nada mal.
15/15