Tema 1 B Valores Medios

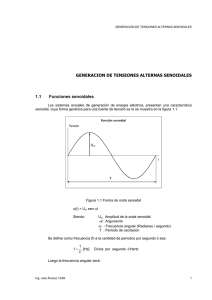
Tema 1 B
Valores Medios - Eficaces
Prof. A. Roldán Aranda
1º Ing. Informática
Repaso de Señales Periódicas
Señales periódicas
v(t)
T
Se cumple:
v(t) = v(t+T)
T = periodo [seg.]
f = 1/T = frecuencia [Hz=s-1]
Definiciones con Señales Periódicas I
Ø Valor medio:
T
1
v = ∫ v (t ) ⋅ dt
T 0
A este valor también se le llama componente de continua
Ejemplo:
v(t)
10
A+
1
2
3
4
5
t(ms)
1
v =
3 ⋅ 10 −3
3⋅10
2⋅10

⋅  ∫ 10 ⋅ dt + ∫ − 20 ⋅ dt  = 0
2⋅10 − 3
 0

−3
−3
A-20
Se dice que una señal es de alterna cuando su
valor medio es nulo
Definiciones con Señales Periódicas II
Ø Valor eficaz:
T
1 2
=
v (t ) ⋅ dt
∫
T 0
Vefi
En inglés: rms (root-mean-square)
Ejemplo:
v(t)
10
1
2
3
4
5
t(ms)
Vefi =
1
4 ⋅ 10 −3
4⋅10
2⋅10 2

2
 ∫ 10 ⋅ dt + ∫ (− 10 ) ⋅ dt  = 10
 0

2⋅10 − 3
−3
−3
-10
Es el valor más comúnmente empleado en circuitos con señales senoidales
Definiciones con Señales Periódicas II
Ø Valor eficaz o RMS de una señal AC es el valor de tensión DC necesaria a aplicar
a una carga resistiva para que produzca la misma disipación de energía que si
Conectásemos es misma carga resistiva a la señal AC en cuestión.
En
el caso de una corriente alterna sinusoidal (como lo es, con
bastanteaproximación, la de la red eléctrica) con una amplitud máxima o de
pico Imax, el valor eficaz Ief es
En el caso de una señal triangular con una amplitud máxima Amax, el valor eficaz
Aef es
Señales Sinusoidades I
Señales periódicas: señales senoidales
v(t) = A·sen(ω·t)
A = amplitud (o valor de pico)
A
2·A = valor pico a pico
ω = frecuencia angular
t
ω ⋅T = 2π
T
è ω=
2π
T
ω = 2π ⋅ f
Valor eficaz de una señal senoidal:
T
Vefi
1
2
2
(ω ⋅ t ) ⋅ dt =
A
sen
=
⋅
T ∫0
1
2π
ω ⋅t = θ
2π
∫A
2
⋅ sen (θ ) ⋅ dθ =
2
0
sen 2 (θ ) =
1 A2
A
⋅
⋅ 2π =
2π 2
2
1 − cos(2 ⋅ θ )
2
Vefi =
A
2
Señales Sinusoidades II
Definición de desfase en señales senoidales:
v1
v2
v1(t) = V1·sen(ω·t)
t
v2(t) = V2·sen(ω·t-ϕ)
v2 está retrasada un ángulo ϕ respecto a v1