Capítulo 4 - prof.usb.ve.

Capítulo 4:
4.1
Estimadores Paramétricos y Estimadores de Estado
de la Máquina de Inducción.
Introducción
En el capítulo anterior se han presentado y discutido varios modelos en
régimen permanente y transitorio de la máquina de inducción. Para utilizar estos
modelos es necesaria la determinación de sus parámetros respectivos. Una vez
que los parámetros son conocidos, el modelo puede evaluar el comportamiento
físico de las diferentes variables de estado de la máquina, dentro del grado de
aproximación permitido por las hipótesis simplificadoras iniciales.
La estimación de estado se utiliza frecuentemente en los sistemas de control
automático, para determinar variables difíciles de medir o para reducir las
incertidumbres y los errores introducidos por los dispositivos de medición. En las
máquinas de inducción resulta de gran interés determinar el par eléctrico, así como
la magnitud y dirección de la amplitud del flujo resultante en el entrehierro. El
conocimiento de estas variables simplifican las acciones de control sobre las
fuentes de alimentación de la máquina, y aceleran el seguimiento de las consignas.
Puede resultar estraño incluir en el mismo tema los procesos de estimación
paramétrica con los métodos de estimación de estado, pero es necesario destacar
que el éxito de estos últimos, depende fundamentalmente de la precisión de los
primeros. La relación existente entre estas técnicas es tan estrecha que resulta
lógico tratar el problema en su conjunto. Los accionamientos de las máquinas de
inducción deben integrar de forma armoniosa estos conceptos, si pretenden
competir con los accionamientos clásicos, o con las nuevas ideas.
Tal vez el problema más simple de la estimación de los parámetros del
modelo de la máquina de inducción consiste en desarrollar algoritmos
automáticos, que determinen con cierta precisión los parámetros del circuito
equivalente clásico. Este problema se viene estudiando desde hace mucho tiempo,
y en la actualidad el desarrollo de las herramientas de cálculo personales permiten
su solución rápida y precisa. Sin embargo, las técnicas simples que se empleaban
en el pasado, pueden tener en muchos casos un ámbito de aplicación muy
importante todavía. Las técnicas aproximadas basadas en simplificaciones del
circuito equivalente o del diagrama de círculo de la máquina de inducción, son
-1-
suficientes para ciertas aplicaciones, o pueden servir de punto de arranque a
métodos numéricos más elaborados.
Los modelos dinámicos de la máquina de inducción dependen de los
mismos parámetros que el circuito equivalente clásico. Esto hace pensar con cierta
lógica en la posibilidad de utilizar las mismas técnicas de estimación paramétrica
que se emplean en el circuito equivalente para determinar los parámetros de los
modelos transitorios. Sin embargo, los modelos dinámicos están orientados a otro
tipo de aplicaciones. En estas aplicaciones los parámetros no pueden considerarse
estáticos o inmutables. Cuando la variación dinámica de los parámetros con las
condiciones de operación de la máquina son importantes, es necesario utilizar
técnicas de estimación mucho más rápidas y refinadas. Las técnicas modernas de
medición y adquisición de datos en tiempo real hacen posible nuevos métodos de
medida. En algunos casos es necesario realizar una adaptación permanente de los
parámetros del modelo a medida que el proceso transcurre y las condiciones de
operación cambian. Se han desarrollado varios métodos aplicables a la solución de
este importante problema [6,27,46,47,61]. Recientemente algunos autores han
aplicado las técnicas de estimación para resolver el problema [17,41,58,71]. En este
trabajo se presentan algunas ideas originales, que pueden simplificar y acelerar los
métodos propuestos anteriormente.
Tanto la estimación de estado como la estimación paramétrica utilizan las
técnicas básicas de la optimización matemática de funciones [9,23,65]. Cuando las
funciones que se desean optimizar no son lineales, el problema se complica
notablemente [23]. Los métodos numéricos de optimización ofrecen en muchos
casos alternativas satisfactorias para abordar este problema, pero cuando el
tiempo de solución es una variable crítica, intentar la formulación mediante
funciones lineales es una alternativa más deseable. En este capítulo se comparan y
discuten los diferentes métodos propuestos, con la intención de presentar
lineamientos concretos sobre el ámbito y alcance de aplicación de cada uno.
-2-
4.2
Estimación de los parámetros del circuito equivalente clásico de la máquina
de inducción por métodos convencionales aproximados.
El circuito equivalente clásico de la máquina de inducción con rotor
bobinado está definido por seis parámetros o elementos circuitales, tres resistencias
que modelan las pérdidas en el cobre de los conductores y en el material
magnético, y tres reactancias que representan los flujos de dispersión y de
magnetización de la máquina. Para modelar máquinas de inducción con rotores
de jaula de ardilla con barras profundas o doble jaula, son necesarios ocho o más
parámetros circuitales [49,52].
El circuito equivalente clásico de la máquina de inducción es semejante al de
un transformador con carga resistiva variable. Por esta razón, la metodología
utilizada en la determinación de los parámetros del circuito equivalente del
transformador se puede aplicar con ciertas variaciones a la estimación aproximada
de los parámetros del circuito equivalente de la máquina de inducción.
Las diferencias fundamentales entre los transformadores y las máquinas de
inducción son dos: por un lado la posibilidad de movimiento relativo entre la
pieza del estator y la del rotor, y por otro la presencia del entrehierro necesario
para permitir este movimiento. En los transformadores convencionales, la
corriente de magnetización es muy pequeña en comparación con la corriente
nominal, por esta razón se puede despreciar esta rama del circuito equivalente,
cuando se desea identificar el valor de las reactancias de dispersión. En la
máquina de inducción esta hipótesis o aproximación es más difícil de sostener
porque el entrehierro hace necesario un mayor consumo de fuerza magnetomotriz
para forzar la circulación del flujo magnético.
Es frecuente que en los
transformadores se tenga asceso a los terminales primarios y secundarios de las
bobinas. Sin embargo, en la mayoría de las máquinas de inducción el acceso a los
circuitos rotóricos no es posible, al menos en condiciones normales.
Para identificar los parámetros del circuito equivalente de un
transformador, se realizan los ensayos normalizados de vacío y cortocircuito
[52,66,73]. El primero con la finalidad de obtener la reactancia y resistencia de
magnetización, y el segundo para determinar las reactancias de dispersión y
resistencias de los conductores. La separación de la resistencia del circuito
-3-
primario y del circuito secundario se pueden realizar midiendo la caída de tensión
al inyectar una corriente continua determinada en una de las dos bobinas. La
separación entre las reactancias de dispersión primaria y secundaria se obtiene
repartiendo proporcionalmente a la reactancia de dispersión total, la reluctancia
del camino magnético en cada bobina. En los transformadores cuyos circuitos
primarios y secundarios tienen la misma potencia aparente, las bobinas ocupan
prácticamente el mismo volumen. En el sistema adimensional de unidades sistema en por unidad -, las dos reactancias de dispersión del modelo T del
transformador son aproximadamente iguales. En valores físicos, la razón entre
estas reactancias es igual al cuadrado de la relación de vueltas del transformador.
En la máquina de inducción la situación es diferente, debido a que las ranuras y los
caminos magnéticos de las bobinas del estator y del rotor pueden ser diferentes.
A pesar de las diferencias existentes entre los modelos clásicos del
transformador y de la máquina de inducción, la primera aproximación en el
problema de la estimación paramétrica consiste en utilizar exactamente las mismas
hipótesis empleadas para los transformadores. Según esta idea, se realizan los
ensayos de vacío y rotor bloqueado de la máquina de inducción para obtener una
estimación paramétrica aproximada del modelo. El ensayo de rotor bloqueado es
equivalente a la prueba de cortocircuito de un transformador. Además de estos
dos ensayos puede ser conveniente o necesaria la realización de ensayos
adicionales en carga.
En el ensayo de vacío se hace girar el rotor de la máquina a una velocidad
angular que sea prácticamente igual a la velocidad sincrónica, de preferencia
mediante un accionamiento externo. De esta forma el deslizamiento entre la
velocidad angular del campo magnético rotatorio del estator y la velocidad angular
mecánica del rotor es nulo. En estas condiciones la fuerza electromotriz inducida
en los conductores del rotor es cero y no circula corriente por estos circuitos. La
máquina se alimenta a frecuencia y tensión nominal en el estator y se miden con la
mayor precisión posible las corrientes por las fases, tensiones de línea y potencia
activa de entrada. Como el circuito es fuertemente inductivo es conveniente
utilizar vatímetros especiales para medir bajos factores de potencia durante el
ensayo. Estos instrumentos son vatímetros normales que producen una deflexión
de la aguja unas cinco veces mayor que la de un vatímetro convencional similar. Si
se utilizan instrumentos digitales, esta precaución no es necesaria. En la figura 4.1
-4-
se presenta el diagrama esquemático del equipamiento requerido para la
realización de este ensayo.
R
+
+ W1 -
Ia
IR
x y z
V
IS
VVW
M.I.
3φ
W
+ W2 +
M.C.C
Va
Ic
T
RPM
U
VUV
S
+
IT
-
Fig. 4.1 Montaje experimental para el ensayo de vacío con accionamiento externo
del eje de la máquina
La tensión en la rama de magnetización es aproximadamente igual a la
tensión de alimentación, debido a que las corrientes de magnetización no producen
una caída significativa en la rama serie del modelo, aun cuando está comprendida
entre una tercera parte y la mitad de la corriente nominal. Con esta simplificación,
la resistencia y reactancia de magnetización se calculan de la siguiente forma:
S0 = 3 V 0 I0
4.1
P 0 = P1 + P 2
4.2
Q 0 = S02 − P02
4.3
Rm ≈
Xm ≈
V 02
V 02
P0
4.4
Q0
4.5
El ensayo de rotor bloqueado consiste en trabar el rotor de la máquina de
inducción. Cuando el rotor está detenido, el deslizamiento es unitario. El circuito
equivalente en estas condiciones de operación es semejante al de un transformador
-5-
en la condición de cortocircuito. En la identificación de los parámetros del circuito
equivalente del transformador se puede despreciar la rama de magnetización,
porque la corriente de cortocircuito es mucho mayor que la corriente de
magnetización. La tensión de la rama de magnetización se deprime prácticamente
a la mitad de la tensión de vacío y esto reduce aún más la corriente que circula por
ella durante el ensayo. En el transformador, la influencia de la rama de
magnetización durante la prueba es prácticamente despreciable.
En la máquina de inducción la corriente de rotor bloqueado puede alcanzar
entre tres y seis veces la corriente nominal. La corriente de vacío está comprendida
entre la tercera parte y la mitad de la corriente nominal. Durante la prueba de
rotor bloqueado la tensión de la rama de magnetización se deprime más o menos a
la mitad, y por esta razón la corriente de la máquina durante este ensayo puede
alcanzar a ser entre seis y dieciocho veces mayor que la corriente de
magnetización. Desde un punto de vista práctico es posible despreciar esta rama
en la estimación de los parámetros. Sin embargo la aproximación no es tan precisa
como cuando se aplica en el ensayo de cortocircuito de un transformador [73].
El esquema de medida es similar al ilustrado en la figura 4.1, pero en lugar
de hacer girar la máquina de inducción a velocidad sincrónica, es necesario
bloquear mecánicamente el rotor. Como el circuito equivalente en este ensayo
también es muy inductivo, deben utilizarse vatímetros de bajo factor de potencia
para mejorar la precisión de la medida, o instrumentos digitales que eliminan este
inconveniente. En la práctica, el ensayo de rotor bloqueado no se realiza a valores
nominales de tensión para evitar el calentamiento excesivo debido al incremento
de las pérdidas con el cuadrado de la corriente, que además se ve afectado
adicionalmente por la falta de ventilación en las máquinas cuyo ventilador se
encuentra acoplado directamente al eje mecánico. De cualquier forma, es necesario
utilizar una tensión suficientemente grande como para que el circuito magnético
esté operando en la zona lineal.
Aun cuando el ensayo a rotor bloqueado se realice con cierta rapidez, la
resistencia de las bobinas cambia apreciablemente con la temperatura y es
necesario corregir las medidas realizadas por este importante factor. Para este fin,
se miden las resistencias del estator cuando la máquina está a temperatura
ambiente, antes de comenzar el ensayo. Esta medida se realiza inyectando
corriente continua en las bobinas y se mide la caída de tensión correspondiente. La
-6-
corriente inyectada debe ser menor a un décimo de la corriente nominal para que
el calentamiento sea prácticamente despreciable. Posteriormente se efectúa el
ensayo a rotor bloqueado, e inmediatamente después de terminar estas medidas,
se realiza una nueva medida de las resistencias del estator, por el mismo método
descrito anteriormente. Las dos medidas de resistencia, y el conocimiento del
material utilizado en el bobinado de la máquina -normalmente cobre recocido en
frío- permiten deducir la temperatura alcanzada por la máquina durante el ensayo.
Si la máquina está bobinada con cobre recocido en frío, la ecuación que determina
la variación de la resistencia en función de las temperaturas es la siguiente [31]:
RT 1
RT 2
=
234.5 + T1 (°C)
234.5 + T2 (° C)
4.6
Para determinar los parámetros de la rama serie del circuito equivalente de
la máquina de las medidas de potencia, tensión y corriente se utiliza el siguiente
procedimiento:
Scc = 3 V cc I cc
2
4.7
2
Qcc = S cc − P cc
4.8
R T ≈ Re + R r' =
Pcc
X T ≈ X e + X r' =
Qcc
3 Icc2
3 Icc2
4.9
4.10
Las resistencias se pueden corregir desde la temperatura de la prueba, a la
temperatura nominal de operación. Como además se conoce la resistencia del
estator por medición directa, la resistencia del rotor referida al estator se calcula
por diferencia:
R r' ≈ R T − R e ≈
Pcc
Con las medidas realizadas, no es
reactancias de fuga del estator y rotor,
dividirlas por igual en las dos ramas. Sin
caminos de fuga del estator y del rotor
-7-
3I cc2
− Re
4.11
posible obtener una separación de las
la práctica más habitual consiste en
embargo, es necesario recordar que los
son diferentes. Los caminos de fuga
dependen de las formas de las ranuras, y estas puede diferir entre el estator y el
rotor de una misma máquina.
Los ensayos tradicionales de vacío y rotor bloqueado aplicados a la máquina
de inducción no pueden determinar completamente los seis parámetros del
circuito equivalente clásico. Cada uno de estos ensayos puede establecer tan solo
dos ecuaciones independientes. Son necesarios ensayos adicionales para la
determinación precisa de todos los parámetros. La medida directa de la resistencia
de las bobinas del estator elimina una incognita, pero todavía es necesaria una
ecuación adicional. Considerar que las reactancias de dispersión del estator y la
del rotor referida al estator son iguales, proporciona una de las aproximaciones
más generalizadas. Si se requiere mayor exactitud es necesario realizar alguna
prueba adicional tal como el ensayo de la máquina en un punto de operación
cercano al nominal. Como los parámetros de la máquina varían durante la
operación, y dependen de la velocidad del rotor, debido principalmente al efecto
pelicular, el sistema de ecuaciones no lineales que se obtiene de tres ensayos a
diferentes velocidades o deslizamientos, puede no ser compatible. Una solución
puede ser incrementar los parámetros del modelo para representar este fenómeno.
Otra solución consiste en obtener el conjunto de parámetros que minimiza una
cierta función de costo constituida por los errores entre las medidas reales y los
valores calculados por el modelo [23,71,73].
En cualquier caso, es un buen criterio determinar cada parámetro de aquel
ensayo que lo representa o sensibiliza mejor. Los parámetros de la rama de
magnetización son protagonistas durante la prueba de vacío. La reactancia de
dispersión es la limitante fundamental de la corriente durante el ensayo a rotor
bloqueado. La resistencia del rotor es la responsable de la transferencia de
potencia y par electromecánico al eje de la máquina, por esta razón los ensayos en
carga y los datos nominales de placa suministran información valiosa sobre este
importante parámetro.
En ocasiones se dispone de muy poca información sobre una determinada
máquina, incluso puede ser posible que se cuente solamente con los datos de placa.
Para determinar en forma gruesa los parámetros de esta máquina cuando no es
posible realizar ensayos, se procede de la siguiente forma:
-8-
•
Se supone que toda la corriente de magnetización es prácticamente reactiva,
con lo cual se desprecia la resistencia de magnetización. Se considera que
esta corriente debe ser aproximadamente, un tercio de la corriente nominal.
•
La corriente nominal, en módulo y ángulo puede determinarse de los datos
de placa. La diferencia entre las corrientes nominal y la corriente de
magnetización es la corriente que circula por la rama rotórica del circuito
equivalente. Esta corriente tiene que transmitir la potencia al eje mecánico a
través de la resistencia del rotor.
•
La potencia nominal en el eje, la corriente por la rama rotórica y el
deslizamiento nominal determinan directamente la resistencia del rotor
referida al estator.
•
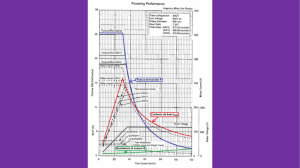
Para determinar aproximadamente la reactancia de dispersión total de la
máquina, se recuerda del lugar geométrico de las corrientes de la máquina
de inducción, que la bisectriz entre dos puntos del diagrama pasa por el
centro del círculo. Como se ha despreciado la resistencia de magnetización,
la dirección de la corriente de magnetización también pasa por el centro del
círculo. La intersección de estas dos líneas es el centro. En la figura 4.2 se
muestra la determinación del diámetro del círculo por este procedimiento.
Recordando que el diámetro del círculo es aproximadamente igual al
cociente entre la tensión aplicada y la reactancia de dispersión total, se
puede determinar fácilmente este parámetro. Finalmente, se pueden hacer
consideraciones sobre el rendimiento de la máquina para obtener una
aproximación a la resistencia del estator.
-9-
Vth
In
Io
Vth /2X th
-j
Fig. 4.2 Obtención de la reactancia de dispersión aproximada a partir de los datos
de placa de la máquina de inducción
4.3
Estimación de los parámetros del circuito equivalente clásico de la máquina
de inducción utilizando técnicas de optimización no lineal.
En la sección anterior se presentó el método aproximado que permite la
determinación de los parámetros del circuito equivalente clásico de la máquina de
inducción. Esta técnica es una adaptación del procedimiento convencional para la
estimación de los parámetros del circuito equivalente del transformador. Con los
ensayos de vacío y rotor bloqueado, se realiza la medida de la impedancia
equivalente de la máquina en dos condiciones de operación, correspondientes a los
deslizamientos cero y uno respectivamente. Además se realiza una medida directa
de la resistencia del estator. Conocida la resistencia del estator, sólo quedan por
determinar cinco parámetros. Cada uno de los ensayos permite establecer dos
ecuaciones, una para la parte real y otra para la parte imaginaria de la impedancia
de entrada. En total, se dispone de cuatro ecuaciones y cinco parámetros
desconocidos.
El problema matemático está indeterminado. La solución obtenida con tan
escasa información, además de utilizar simplificaciones más o menos razonables,
debe considerar una separación artificial de las reactancias de dispersión. Este
- 10 -
problema se puede resolver realizando ensayos adicionales a diferentes
deslizamientos. Con estos ensayos, se obtiene un sistema con un mayor número de
ecuaciones - dos por cada ensayo -. Como los parámetros que se están
determinando son siempre cinco, se tienen más ecuaciones que incógnitas. El
sistema de ecuaciones obtenido está sobre determinado. Las medidas realizadas
en los ensayos incluyen errores de apreciación del observador y precisión en los
instrumentos. Los parámetros de la máquina varían durante la operación,
dependiendo de variables tales como el grado de saturación, la temperatura y el
efecto pelicular entre otras. Además, el modelo es una aproximación en la cual se
realizan varias hipótesis simplificativas, que es válido solamente en un régimen de
operación perfectamente equilibrado. En esta situación, resulta de gran utilidad la
técnica de estimación paramétrica por el método de los mínimos cuadrados [71].
Del circuito equivalente de la máquina de inducción se puede determinar la
impedancia de entrada en función de los parámetros de la máquina, la frecuencia
de alimentación y el deslizamiento del rotor. La función de impedancia de entrada
vista en bornes del estator tiene la siguiente estructura:
Z e ( Re , Lσe , Rr , Lσr , Rm , Lm , s, ω e ) = Zσe + Zσr || Z m = Zσe +
donde:
Z σr Z m
Z σr + Z m
4.12
Zσe = Re + jω e Lσe
4.13
Zσr = Rr + jω e Lσr
4.14
Z m = Rm || jX m =
jω e Lm Rm
Rm + jω e Lm
4.15
Si se utiliza el modelo de impedancia de entrada de la máquina obtenido en
la expresión 4.12, realizando n ensayos independientes con una cierta precisión,
para lo cual se varía la velocidad del rotor o la frecuencia de alimentación, el
problema que se debe resolver para determinar los parámetros del circuito
equivalente clásico de la máquina de inducción consiste en:
Minimizar Ψ:
 Z ( s , ω ) − Z emed i ( si , ω ei )   Z ecali ( si , ω ei ) − Z emed i ( si , ω ei ) 
ψ = ∑  ecali i ei


σ i .Z emed i ( si , ω ei )
σ i .Z emed i ( si , ω ei )
i =1 
 


n
- 11 -
*
4.16
donde:
Z e medi i-ésima impedancia medida en los ensayos.
Z e cali i-ésima impedancia calculada mediante el modelo.
si
ωi
σi
i
n
deslizamiento de la i-ésima medida.
frecuencia de la i-ésima medida.
factor de precisión de la medida i.
número correspondiente a cada medida, y
número total de medidas.
La ecuación 4.16 se puede escribir matricialmente como:
ψ = f T * .f ,
4.17
f T * = [f *1 (x , s 1 , ω e 1 ) f *2 (x , s 2 , ω e 2 ) … f *n (x , s n , ω en )],
4.18
donde:
f i (x ,si , ω ei ) =
Ze cali ( x, si , ω ei ) − Ze med i (x ,si , ω ei )
σ i . Ze med i (x ,si , ω ei )
x T = [R e Lσ e R r
Lσr
,y
Lm ]
Rm
4.19
4.20
Considerando que la ecuación 4.17, no es lineal en el caso general, las
derivadas parciales de la función de costos ψ con respecto a cada una de los
parámetros del vector x del modelo, se calculan de la siguiente forma:
T*
 ∂ f T * ( x) 
 ∂ψ (x) 
 ∂ f (x)   ∂ f (x) 
T*
T
(
)
(
).
.
2
=
G
x
=
f
x
+
f
=
 ∂ x  .f (x) = 2.J (x).f (x) 4.21
 ∂ x 
 ∂ x   ∂ x 




La matriz J(x) definida en la ecuación 4.21 es la matriz Jacobiana del vector de
errores ponderados f(x) . La matriz Jacobiana es de dimensión nxm, donde n es el
número de medidas, y m el número total de variables de estado o parámetros del
modelo.
El incremento de los parámetros que minimiza la función de costos 4.17,
cuando se utiliza el método de optimización de Gauss-Newton [23,65] es de la
siguiente forma:
[
]
−1
∆ x = − J(xk ) . J(x k ) . J(x k ) .f (xk )
T
- 12 -
T
4.22
Y el vector de variables de estado o parámetros del modelo en la iteración k+1 se
calcula como:
x k +1 = x k + ∆ x
4.23
Si en la iteración k , el módulo del vector ∆x es menor que un cierto error ε
especificado inicialmente, el problema converge al mínimo local más cercano de la
función de costos ψ . Este método presenta ciertos problemas de convergencia, en
particular cuando el peso de las segundas derivadas en la matriz Hessiana es
importante. Para garantizar la convergencia del método es recomendable
modificar la ecuación 4.23 de la siguiente forma:
x
k +1
= x + α . ∆x
k
4.24
Sustituyendo la ecuación 4.24, en el vector de errores ponderados f (x k +1 ) se
puede obtener mediante la ecuación 4.17, la función de costos para la iteración
k + 1 , en función de las variables de estado obtenidas en la iteración k , y el
parámetro unidimensional α :
ψ (x k +1 ) = ψ (x k + α . ∆x) = f (x k + α .∆x) .f (xk + α .∆x )= ψ (α )
T
4.25
Para obtener el nuevo vector de corrección α . ∆x , es necesario determinar el
valor del parámetro α que minimiza la función de costos.
Una vez obtenido el valor de las variables de estado que minimizan la
función de costos en la iteración k + 1 , se prosigue el cálculo determinando una
nueva dirección mediante la ecuación 4.22, y un nuevo proceso de búsqueda del
mínimo con la expresión 4.25. Cuando el módulo del vector de dirección es
inferior a la precisión requerida en los cálculos, culmina el proceso de
minimización obteniéndose la mejor estimación de los parámetros del modelo. En
la figura 4.3 se presenta el algoritmo básico de este proceso de estimación
paramétrica.
- 13 -
Lectura de:
- Nº de medidas 'n'
- deslizamiento s i
- frecuencia ωei
- impedancia Zmi
k=0
Cálculo de los valores
iniciales del vector x k
Evaluación de J
k=k+1
no
T
g (x k) = 2 J f
T
H (x k) ≅ 2 J J
-1
∆xk = - H g
k>k
max
si
xk+1 = xk + α ∆xk
si
Fin
no
¿Otra
Solución?
si
¿| ∆x | < ε?
no
Obtención de a que
min. Ψ (x + α ∆x)
búsqueda lineal
Fig. 4.3 Diagrama de flujo del método de minimización de Gauss-Newton
Uno de los inconvenientes que presenta el método de Gauss-Newton
modificado es la necesidad de encontrar un valor inicial para las variables de
estado. La función de costos ψ , puede tener múltiples mínimos locales. La mejor
solución para el modelo es aquella que produce el menor de los mínimos locales.
Los valores de arranque pueden ser generados mediante una estimación inicial de
tipo determinístico que puede ser realizada mediante los métodos tradicionales
simplificados analizados en la sección anterior. De todas formas, el método de
Gauss-Newton requiere de un valor inicial cercano a la solución para garantizar la
convergencia a la solución óptima.
Si se desea asegurar la convergencia del método, es conveniente limitar la
corrección máxima α ∆x k para que ninguno de los parámetros de la máquina
- 14 -
definidos en el vector x k pueda aumentar o disminuir en más de un cincuenta por
ciento en cada paso o iteracción del proceso de optimización. Esto puede reducir
la velocidad del algoritmo, pero asegura que los parámetros han de ser siempre
positivos, y evita las posibles divergencias originadas por la no linealidad del
modelo.
El método de Gauss-Newton es muy eficiente para la determinación de los
parámetros cuando la función de costos se define por mínimos cuadrados. Otros
métodos de optimización no lineal también pueden obtener soluciones con más o
menos dificultad. Como ejemplo, se presenta a continuación el listado de un
algoritmo realizado en el entorno de programación MATLAB versión 3.5. En este
ejemplo se realiza la estimación de los parámetros del modelo de una máquina de
inducción de rotor bobinado. Para validar la herramienta se definen los valores de
las resistencias e inductancias del circuito equivalente. Con estos parámetros se
evalúan las impedancias de entrada de la máquina para las condiciones de la
prueba de vacío, carga y rotor bloqueado. Por el método aproximado descrito en
la sección anterior, se realiza una estimación inicial de los parámetros. Se utiliza
un programa de la librería del entorno denominado ‘fmins’ que utiliza la
modificación al método Simplex de Nelder-Meade [39].
Ejemplo 1: Estimación paramétrica de la máquina de inducción de rotor
bobinado.
%************************************************************
% Estimación de los parámetros de una máquina de inducción
% mediante la técnica de los mínimos cuadrados.
%************************************************************
% programa parámetros.
% Para este ejemplo se utilizó el circuito equivalente para
% determinar la impedancia de entrada para tres deslizamientos
% diferentes: vacío (s=0), carga (s=0.03) y rotor bloqueado (s=1)
% Los parámetros del circuito equivalente de esta máquina son:
%
%
Re = .02 p.u.
Xe = .10 p.u.
%
Rm = 50. p.u.
Xm = 3.0 p.u.
%
Xr = .15 p.u. Rr = .03 p.u.
%
% Los ensayos realizados dieron los siguientes resultados:
%
%
Zmedida(s=0)
= .199350+j3.0892 p.u.
%
Zmedida(s=0.03) = .833740+j.49141 p.u.
%
Zmedida(s=1)
= .047603+j.24296 p.u.
%
Re
= .02 p.u. (Medida directa)
%
% Utilizando el método aproximado se consiguen los siguientes
% valores de arranque.
%
%
Xeo = .12
p.u.
Rmo = 48.0 p.u.
%
Xmo = 3.3
p.u.
Xro =.12
p.u.
%
Rro = .0276 p.u.
- 15 -
%
% Estos valores se cargan en el vector de arranque x0:
%
x0 = [.12 48. 3.3 .0276 .12];
%
% Finalmente se llama a la rutina ’fmins’ que calcula los valores
% de los parámetros x que minimizan la función de costo.
% El error relativo especificado para la convergencia es 0.001
%
x = fmins('costo', x0, 0.001);
%
% En el vector x se han cargado los parámetros óptimos de la
% estimación. La solución es:
%
Refin = 0.02
Xefin = x(1)
Rmfin = x(2)
Xmfin = x(3)
Rrfin = x(4)
Xrfin = x(5)
%
% Fin del cálculo paramétrico.
%************************************************************
function Fi = costo(x)
%************************************************************
%
% Evaluación de la función de costos por mínimos cuadrados.
% Fi = Sumatoria(errores relativos)^2
%
% Deslizamientos correspondientes a los ensayos de vacío,
% carga y rotor bloqueado.
%
s = [1e-10 .03 1.];
%
Re = 0.02; % Medición directa de la resistencia estator
Xe = x(1); % Reactancia de dispersión del estator
Rm = x(2); % Resistencia de magnetización
Xm = x(3); % Reactancia de magnetización
Rr = x(4); % Resistencia del rotor referida al estator
Xr = x(5); % Reactancia dispersión rotor referida al estator
%
% Vector fila de las impedancias de entrada medidas en los
% ensayos.
%
Zmedida = [1.9935e-01-3.0892e+00*i
8.3374e-01-4.9141e-01*i
4.7603e-02-2.4296e-01*i]';
%
% Evaluación de las impedancias calculadas mediante la estimación
% de los parámetros del modelo.
%
Ze = Re+j*Xe;
Zm = (Rm*j*Xm)/(Rm+j*Xm);
Zth = Ze*Zm/(Ze+Zm)+j*Xr;
Ve = 1.00;
Vth = Zm*Ve/(Zm+Ze);
Ir = Vth./(Zth+Rr./s);
Ee = Ir.*(Rr./s+j*Xr);
Im = Ee./Zm;
Ie = Im+Ir;
Zcalculada=Ve./Ie;
% Impedancia estator
% Impedancia magnetización
% Impedancia de Thevenin
% Tensión del estator
% Tensión de Thevenin
% Corriente del rotor referida
% Tensión rama magnetizante
% Corriente de magnetización
% Corriente del estator
% Impedancia de entrada
% calculada
%
% Cálculo del error relativo entre las medidas y el modelo
%
- 16 -
error = (Zmedida-Zcalculada)./Zmedida;
%
% Cálculo de la función de costo por mínimos cuadrados
%
Fi = error*error';
%
% Fin de la función 'costo'
%************************************************************
% Resultados obtenidos al ejecutar el programa ...
%************************************************************
»parámetros
Refin
Xefin
Rmfin
Xmfin
Rrfin
Xrfin
»
= 0.0200
= 0.0999
= 50.0014
= 3.0000
= 0.0300
= 0.1501
En la siguiente tabla se presenta una comparación entre los resultados de los
dos métodos:
Parámetro
Método
Aproximado
Estimación
MATLAB
Exacto
Re
Xe
Rm
Xm
R ’r
X’r
0.0200
0.0200
0.0200
0.1200
0.0999
0.1000
48.000
50.0014
50.000
3.3000
3.0000
3.0000
0.0276
0.0300
0.0300
0.1200
0.1501
0.1500
Si la máquina de inducción posee un rotor de jaula de ardilla de barra
profunda o de doble jaula, es necesario modificar el cálculo de la impedancia de
entrada, e incrementar el número de ensayos linealmente independientes. En la
figura 4.4 se ha representado el modelo circuital de la máquina de inducción con
rotor de doble jaula, este modelo se utiliza también para analizar, en una primera
aproximación, el comportamiento de las máquinas con rotor de jaula de ardilla con
barras profundas [49,52].
- 17 -
Ze
Re
Zr
j Xe
Rm
Z entrada
j Xr 2
j Xr 1
j Xm
Rr 1
s
Rr 2
s
Zm
Fig. 4.4 Modelo de la máquina de inducción con rotor de doble jaula
La impedancia de entrada de una máquina de doble jaula se puede calcular,
a partir del modelo de la Fig. 4.4 como:
Z entrada = Ze +
donde:
Z r ⋅ Zm
Zr + Z m
Z e = R e + jX e
Zm =
jR m ⋅ X m
R m + jX m
Rr1
⋅Z r2
+ jX r1 , y
Z r = Rs
r1
+ Zr 2
s
Z r2 =
Rr 2
s
+ jX r2
4.26
4.27
4.28
4.29
4.30
Para determinar los ocho parámetros de este modelo son necesarios al
menos cuatro ensayos independientes. En estas pruebas las variables de control
pueden ser el deslizamiento y la frecuencia de alimentación. Los valores iniciales
de los parámetros del modelo se obtienen simplificando el circuito equivalente en
cada una de las condiciones de ensayo.
- 18 -
Ejemplo 2: Estimación parcial de los parámetros de la máquina de inducción
de doble jaula
%************************************************************
% Estimación de los parámetros de una máquina de inducción de
% doble jaula mediante la técnica de los mínimos cuadrados.
%************************************************************
%
% Para este ejemplo se utilizó el circuito equivalente para
% determinar la impedancia de entrada para cuatro
% deslizamientosdiferentes: vacío (s=0), carga (s=0.03 y 0.06)
% y rotor bloqueado (s=1)
%
% Los parámetros reales del circuito equivalente de esta máquina
% son:
%
Re = .02; Xe = .10;
Rm = 50.;
Xm = 3.0;
Xr1= .10; Rr1 =.08;
Xr2 = .15; Rr2 = .04;
%
% Los deslizamientos de los cuatro ensayos son:
%
s=[0.001 .03 .06 1.0];
%
% Los cuatro ensayos realizados dieron los siguientes resultados:
%
% Zmedida=[.5218+3.0114*i .7531+.4558*i .4133+.3103*i .0747+.2217*i]
%
% Utilizando el método aproximado se consiguieron los siguientes
% valores de arranque.
%
%
Reo = 0.02
Xeo = .10
Xmo = 3.00
Rmo = 50.
%
Rr1o = 0.08
Xr1o = .12
Rr2o = 0.03
Xr2o= .12
%
% Se puede suponer para simplificar el proceso de estimación que
% los parámetros del estator son conocidos con precisión. Si se
% cargan las estimaciones del resto de los valores en el vector
% de aranque xo:
%
x0=[.09 .12 .03 .12];
%
% Finalmente se llama a la rutina fmins que calcula los valores
% de los parámetros x que minimizan la función de costo.
% El error relativo especificado para la convergencia es 0.001
%
OPTIONS=[0 .001 .001];
x=fmins('costo2',x0,OPTIONS);
%
% Fin del algoritmo de estimación paramétrica
%************************************************************
function Fi = costo2(x)
%************************************************************
%
% Evaluación de la función de costos por mínimos cuadrados.
% Fi = Sumatoria(errores relativos)^2
%
% Deslizamientos correspondientes a los ennsayos de vacío,
% carga y rotor bloqueado.
%
- 19 -
s = [.001 .03 .06 1.];
%
Re =
Xe =
Rm =
Xm =
Rr1=
Xr1=
Rr2=
Xr2=
0.02;
.1 ;
50 ;
3.0 ;
x(1);
x(2);
x(3);
x(4);
%
%
%
%
%
%
%
%
Medición directa de la resistencia estator
Reactancia de dispersión del estator
Resistencia de magnetización
Reactancia de magnetización
Resistencia del rotor1 referida al estator
Reactancia dispersión1 rotor referida al estator
Resistencia del rotor2 referida al estator
Reactancia dispersión2 rotor referida al estator
%
% Vector fila de las impedancias de entrada medidas en los ensayos.
%
Zmedida=[.5218+3.0114*i .7531+.4558*i .4133+.3103*i .0747+.2217*i];
%
% Evaluación de las impedacias calculadas mediante la estimación
% de los parámetros del modelo.
%
Zr2 = Rr2./s+i*Xr2;
Zr1 = (Rr1*Zr2./s)./(Rr1./s+Zr2)+i*Xr1;
Zm
= i*Rm*Xm/(Rm+i*Xm);
Ze
= Re+i*Xe;
Zcal = Ze+(Zr1*Zm)./(Zr1+Zm);
%
% Cálculo del error relativo entre las medidas y el modelo
%
error = (Zmedida-Zcal)./Zmedida;
%
% Cálculo de la función de costo por mínimos cuadrados
%
Fi = error*error';
%
% Fin de la función 'costo2'
%************************************************************
% Resultados optenidos al ejecutar el programa ...
%************************************************************
» La solución es:
Refin
Xefin
Rmfin
Xmfin
Rr1fin
Xr1fin
Rr2fin
Xr2fin
=
=
=
=
=
=
=
=
0.02
.1
50
3.
7.9822e-02
1.0009e-01
4.0036e-02
1.5020e-01
»
En la siguiente tabla se presenta una comparación entre los resultados de los
dos métodos:
Parámetro
Método
Aproximado
Estimación
MATLAB
Exacto
Re
Xe
Rm
Xm
0.0200
0.0200
0.0200
0.1000
0.1000
0.1000
50.000
50.000
50.000
3.0000
3.0000
3.0000
- 20 -
R’r1
X’r1
R’r2
X’r2
0.0900
0.0798
0.0800
0.1200
0.1001
0.1000
0.0300
0.0400
0.0400
0.1200
0.1502
0.1500
En el ejemplo 2, el proceso de estimación paramétrica se puede acelerar
considerablemente si se determinan directamente los parámetros del estator. Estos
parámetros pueden ser obtenidos con mucha precisión de los ensayos de vacío rama de magnetización-, secuencia cero - reactancia de dispersión del estator-, y
resistencia de las bobinas del estator. En este caso no se han realizado ensayos a
varias frecuencias, pero esto permite discernir con mayor precisión entre los
parámetros del rotor.
Aun cuando la técnica de estimación no lineal conduce a un conjunto de
parámetros que reproduce con gran aproximación el comportamiento de la
máquina, los algoritmos de optimización tienen una convergencia relativamente
lenta desde el punto de vista del tiempo de cálculo requerido. Sin embargo,
cuando la estimación inicial no difiere demasiado de los parámetros de solución, el
proceso se acelera notablemente. Esta idea podría ser empleada en un estimador
paramétrico en tiempo real, fuera de línea se pueden determinar los parámetros de
la máquina con gran precisión, y posteriormente se ajustan a medida que estos
varían de acuerdo con las condiciones de operación. De cualquier forma, la
densidad de cálculo necesaria en esta solución, requiere la utilización de
computadores de muy alta velocidad de procesamiento y lenguajes de
programación de alto nivel - Fortran, Pascal, C, Matlab, etc-. El cálculo de la
impedancia de entrada puede ser efectuado en línea, a partir de las medidas de las
tensiones y corrientes instantáneas obtenidas en bornes de la máquina mediante
transductores adecuados y conversores analógico-digitales relativamente rápidos.
- 21 -
4.4
Estimación paramétrica utilizando modelos dinámicos de la máquina de
inducción.
La principal dificultad en la estimación de los parámetros de la máquina de
inducción estriba en la imposibilidad de medir directamente algunas variables
internas. Los modelos de régimen permanente y transitorio definen parámetros,
corrientes y tensiones que no son accesibles directamente. Por esta razón el
método de estimación desarrollado en la sección anterior, determina un
comportamiento no lineal de la impedancia de entrada. Para resolver este
problema es preciso obtener un sistema de ecuaciones lineales como
representación de la máquina de inducción, y eliminar las variables no medibles.
Esta idea no es nueva, y ha sido utilizada por la teoría de control automático para
caracterizar plantas de gran complejidad [6,27,58,71].
El modelo transitorio de la máquina de inducción en coordenadas
arbitrarias desarrollado en el capítulo 3, se puede expresar como:
δ
di δe
' di r
v e = Re i e + L
+ Ler
+ jδ{L'e i δe + L'er i δr }
dt
dt
δ
δ
'
e
v δr = Rr i δr + L'r
3
2
4.31
di δ
di δr
+ L'er e + j (δ − θ){L'r i δr + L'er i δe }
dt
dt
4.32
{(
4.33
)
*
}
Ler ℑm i δe i δr + τ m = J
dθ
+ α fric.θ
dt
Si la velocidad angular mecánica θ = ω m , es constante, y la velocidad
angular de la referencia arbitraria δ , se considera nula por razones de simplicidad,
las ecuaciones diferenciales 4.31 y 4.32, se convierten en una representación lineal
del comportamiento de la máquina de inducción. Además, en general la tensión
del circuito rotórico es nula:
v e = Re i e + L'e pi e + L'er pi r
{
0 = Rr i r + L'r pi r + L'er pi e − jθ L'r i r + L'er i e
4.34
}
4.35
Despejando de la ecuación 4.35, la derivada de la corriente del rotor pi r y
sustituyéndola en la expresión 4.34, se obtiene:
- 22 -
 Rr 
L'er
L'er
pi r =  jθ − '  i r + jθ ' i e − ' pi e
Lr 
Lr
Lr

4.36
2


L'er 
R 

v e = Re + jθ ' i e + Lˆ'e pi e + L'er  jθ − 'r i r


Lr 
Lr 


4.37
' 2
L
Lˆ'e = L'e − er' .
Lr
donde:
Derivando con respecto al tiempo la expresión 4.37, sustituyendo la
derivada de la corriente del rotor pi r , obtenida a partir de la ecuación 4.36, y
remplazando en la misma expresión la corriente del rotor i r , obtenida a partir de la
propia ecuación 4.37, resulta:



L'
R
pv e = Lˆ'e p 2 i e +  Re + Rr 'e − jθLˆ'e  pi e +  jθ − 'r
Lr
Lr




 v e − Re i e

(
)
4.38
[]
4.39
La expresión 4.38, se puede reescribir de la siguiente forma:
[
]
[ ]
[
]
[ ]
pv e − jθv e = k1 p 2 i e − jθ pi e + k 2 pi e − k 3 jθi e − k 4 v e + k 5 i e
donde:
k1 = Lˆ'e ; k 2 = Re + Rr
L'e
R
R
; k 3 = Re ; k4 = 'r ; k5 = Re 'r
'
Lr
Lr
Lr
4.40
En la ecuación 4.39, el miembro de la izquierda de la igualdad no depende
de los parámetros de la máquina, puede ser evaluado directamente de medidas
instantáneas realizadas en bornes de la máquina. En cambio, el miembro a la
derecha de la igualdad, depende de los cinco coeficientes indicados como
k 1 , k2 , k3 , k4 y k 5 , además de las cinco funciones de variables que también pueden
ser medidas directamente. Esta ecuación requiere de un mínimo de tres medidas
linealmente independientes para poder determinar por regresión lineal estos cinco
coeficientes. Para que las ecuaciones correspondientes a cada medida sean
independientes, es necesario utilizar al menos tres puntos de operación con
diferente carga en eje del rotor.
Para determinar los cinco coeficientes de la ecuación 4.39, se construye una
función de costo con la sumatoria de los errores cuadráticos, entre los valores
medidos que son independientes de los parámetros, y los valores calculados
- 23 -
mediante una cierta estimación. Los parámetros que minimizan la función de
costo son la mejor solución posible al problema planteado. La función de costos se
puede representar de la siguiente forma:
t
n
ψ = ∑   f med ( ti , ω m )  −  f cal ( ti , ω m )   ⋅   f med ( ti , ω m )  −  f cal ( ti , ω m ) 

 

i =1
i
i
i
i
4.41
donde:
 f med ( ti , ω m )  =  pv e − jθ v e  = [ hi ]
i 
i 
 i

 f cal ( ti , ω m )  =  p 2 i e − jθ pi e
i 
i
i


pi ei
jθ i ei
v ei
i ei  [ k1
4.42
k2
k3
k4
k5 ] = [ wi ][ k ]
t
4.43
Calculando las derivadas parciales de la función de costo ψ con respecto a
cada uno de los parámetros k , se obtiene:
t
n
ψ = ∑ [ hi ] − [ wi ][ k ] ⋅ [ hi ] − [ wi ][ k ]
4.44
i =1
n
n
n
 ∂ψ 


=
−
−
=
⇒
=
2
h
w
k
0
h
[
]
[
][
]
[
]
[
]
[ wi ][ k ] ⇒
∑
∑
∑
i
i
 i

 ∂ k 
i =1
i =1
i =1
n
n
n

n

∑ [ wi ] [ hi ] = ∑ [ wi ] [ wi ][ k ] ⇒ ∑ [ wi ] [ hi ] = ∑ [ wi ] [ wi ]  [ k ] ⇒
i =1
t
t
i =1
t
t
 i =1
i =1

4.45
−1
 n
  n

t
t
[ k ] = ∑ [ wi ] [ wi ]  ∑ [ wi ] [ hi ]
 i =1
  i =1

Una vez que el vector de los coeficientes [k ] ha sido obtenido mediante la
expresión 4.45, se pueden determinar los parámetros de la máquina de inducción
utilizando las definiciones 4.40:
2
k 2 − k3
1 L'er
; Tr = ;
Re = k3 ; L =
= L'e − k1
'
k4
k4
Lr
'
e
4.46
La técnica de estimación paramétrica por regresión lineal, se puede utilizar
en tiempo real para adaptar los parámetros del modelo, a medida que las
condiciones de operación determinan posibles variaciones de los mismos. La
inductancia mutua estator-rotor L'er , y la inductancia del rotor L'r , no se pueden
- 24 -
obtener independientemente con esta formulación. Algunos autores sugieren la
posibilidad de incluir una ecuación adicional para eliminar este problema
[12,58,68]. Una posibilidad es la de utilizar el criterio de igualdad entre las
inductancias del estator y del rotor de la máquina. Esta idea no es descabellada y
biene siendo utilizada desde hace mucho tiempo para repartir la reactancia de fuga
del modelo en las dos ramas. Además, el modelo en coordenadas de campo
orientado utiliza solamente los parámetros calculados en la expresión 4.46. Esto
significa que el modelo no pierde información dinámica al realizar esta
consideración.
La estimación independiente de cada uno de los parámetros del modelo, se
puede obtener derivando por segunda vez la ecuación del estator 4.38 [58]. Este
procedimiento tiene por desventaja la necesidad de utilizar derivadas de mayor
orden - primero, segundo y tercero -. La derivación introducen ruidos en el
proceso de estimación, especialmente cuando se realiza a variables medidas y
digitalizadas. También tiene como inconveniente que el sistema de ecuaciones
relaciona los coeficientes [k ] con los parámetros del modelo mediante un sistema
no lineal de ecuaciones algebraicas, cuya solución numérica tiene una
convergencia relativamente lenta cuando se compara con la solución directa
obtenida en la expresión 4.46, para el método con primeras y segundas derivadas.
Lógicamente, esto puede ser más rápido desde el punto de vista de cálculos que la
optimización de funciones no lineales, pero de cualquier modo reduce
considerablemente la aplicabilidad del método.
Para ilustrar la técnica se han estimado los parámetros de un motor de
inducción con rotor de jaula de ardilla con los siguientes datos y valores
nominales:
Pn = 100 Hp
Tn = 570 Nm
Iarr. = 594 A
Vn = 460 V
nn = 1719 rpm
Tarr. = 573 Nm
In = 154 A
cos φn = 0.91
ηn = 0.876
p=4
Conexión en estrella
f = 60 Hz
trifásico
Tm = 1114 Nm
Jeje = 5 Kgm2
Las bases escogidas para la representación del modelo y sus parámetros en
el sistema adimensional de unidades, son las siguientes:
- 25 -
SBASE =123 kVA
ωBASE = 188.5 rps
VBASE = 460 V
TBASE = 682 Nm
IBASE = 154 A
tBASE = 2.7e-3 s
Los voltajes y corrientes de las bobinas del estator, y la velocidad angular
mecánica del rotor se midieron en tres condiciones de operación diferentes. El par
de carga fue diferente en cada punto. Los registros numéricos fueron procesados
para determinar las primeras y segundas derivadas de las variables necesarias.
Algunos registros de interés se presentan a continuación:
tiempo [p.u.]
ωm
[p.u.]
0.0000
2250.0
4500.0
0.0000
0.5000
1.0000
v e [p.u.]
0.0000-j1.4142
0.8213-j1.1513
1.3372-j0.4602
pv e [p.u.]
1.4142-j0.0000
1.1513+j0.8213
0.4602+j1.3372
i e [p.u.]
-5.8091-j2.8707
-1.9584-j5.5378
-0.1281-j0.3696
pi e [p.u.]
2.8707-j5.8091
5.5378-j1.9584
0.3696-j0.1281
5.8091+j2.8707
1.9584+j5.5378
0.1281+j0.3696
2
p i e [p.u.].
Cuando se aplica el procedimiento de regresión lineal 4.45, a los tres
registros de valores independientes de la tabla anterior, se obtienen los siguientes
valores de los coeficientes indeterminados [k ], y de los correspondientes
parámetros del modelo dinámico de la máquina de inducción:
k1
k2
k3
k4
k5
0.1952
0.0986
0.0548
0.0121
6.6308 E-4
Re
Le
'
Tr
L'er / L'r
0.0548
3.6200
82.645
3.4248
2
Considerando que las inductancias propias del rotor y del estator son
prácticamente iguales, se obtiene el siguiente conjunto de parámetros:
Re
Le
'
Ler
'
Lr
'
Rr
0.0548
3.6200
3.5210
3.6200
0.0438
Algunos autores [18,27,47] han utilizado las medidas directas de la potencia
activa o reactiva instantánea, para adaptar el valor de la constante de tiempo del
rotor T r , durante la operación de la máquina. Este método se fundamenta en
determinar el valor de la constante de tiempo del rotor que anula el error entre la
- 26 -
potencia medida en bornes del convertidor y aquella que se calcula mediante el
modelo. El esquema de control adaptivo [27], considera que el único parámetro
del modelo que varía durante la operación de la máquina es la resistencia del rotor.
La integral del error de potencia determina un valor proporcional a la variación de
la constante de tiempo del rotor, necesaria para eliminar el propio error.
Esta idea es útil e interesante, aun más cuando el error se establece
utilizando como base la potencia reactiva instantánea de la máquina, debido a que
en este caso se elimina la dependencia funcional con las resistencias de las bobinas
del estator. Combinando esto con los métodos de estimación paramétrica por
regresión lineal de las ecuaciones diferenciales, reducidas a variables medibles, se
obtiene un método novedoso de estimación paramétrica. Este método utiliza la
regresión lineal, las ecuaciones de potencia activa y reactiva instantanea, y las
respectivas medidas en bornes de la máquina, para eliminar la necesidad de
calcular derivadas de orden mayor a uno.
En un convertidor electromecánico con varios puertos eléctricos, la potencia
instantánea de entrada se define como la sumatoria de los productos de las
tensiones y corrientes en cada uno de los puertos. Para la máquina de inducción
trifásica, se tiene:
p (t ) = v a ⋅ i a + v b ⋅ ib + v c ⋅ i c
4.47
Si la conexión no incluye retorno, se debe cumplir alguna de las siguientes
relaciones:
i a + ib + i c = 0
4.48
v a + vb + vc = 0
4.49
La potencia instantanea, calculada a partir de los vectores espaciales de
tensión y corriente se realiza multiplicando el fasor espacial de la tensión v, por el
conjugado del fasor espacial de la corriente i*, esto con la finalidad de mantener la
convención de potencia reactiva inductiva entrando al puerto del convertidor
como positiva:
- 27 -
s = v.i* = p ( t ) + j q(t ) =
2
va + e j 3 vb + e j 3 vc  ⋅


2π
3
4π
= [ va ⋅ ia + vb ⋅ ib + vc ⋅ ic ] + j
2
ia + e j 3 ib + e j 3 ic  =


4π
3
2π
4.50
1
[ia ⋅ vbc + ib ⋅ vca + ic ⋅ vab ]
3
La parte real de la expresión 4.50, corresponde exactamente con la definición
4.47, de la potencia activa instantánea, el término imaginario se puede asociar al
concepto de potencia reactiva instantánea utilizada por la máquina. Para
interpretar físicamente esta definición, se puede recordar la relación que existe
entre la fuerza electromotriz e , y la intensidad de campo eléctrico E por una parte,
y entre la intensidad de campo magnético H y la corriente i por otra. El producto
vectorial de los campos eléctrico E y magnético H se define como vector de
Pointing P [38,40,60]. El vector de Pointing P representa el flujo de potencia por
unidad de área del campo electromagnético. En un punto determinado del
entrehierro de la máquina, el vector de Pointing P tiene dos componentes, una en
la dirección axial que determina el flujo de potencia entre el estator y rotor, y otra
tangencial que mantiene el campo magnético interno. Como la corriente i y la
intensidad del campo magnético H están relacionados a través de la ley de
Ampère, y la fuerza electromotriz e se obtiene integrando la intensidad del campo
eléctrico E, es razonable pensar que la potencia activa instantánea está
estrechamente relacionada con la componente axial del vector de Pointing P, y que
la potencia reactiva instantánea depende de la componente imaginaria de este
mismo vector. Sin embargo, es necesario recordar que la magnitud y fase del
vector de Pointing P, depende de la posición espacial y del tiempo, mientras que
las potencias activas y reactivas instantáneas solamente son funciones temporales.
Esto es debido a que estas potencias son definiciones macroscópicas que tienen
implícita una integración en el espacio, y el vector de Pointing es la densidad de
potencia en un punto determinado del espacio y del tiempo. Para realizar la
analogía completa con la tensión espacial v en lugar de la fuerza electromotriz e , es
necesario incluir los fenómenos no conservativos, es decir las pérdidas óhmicas en
los conductores.
En el sistema de coordenadas arbitrarias δ = 0;δ = 0 , la potencia activa y
reactiva instantánea es:
- 28 -
s ( t ) = v ( t ) .i* ( t ) = p ( t ) + jq ( t ) = ( vδ .e jδ ) . ( iδ .e jδ ) = vδ . ( iδ ) =
*
*
( vdδ + j vqδ ) .( idδ − j iqδ ) = ( vdδ .idδ + vqδ .iqδ ) + j ( vqδ .idδ − vdδ .iqδ )
4.51
La expresión 4.51 es válida para cualquier sistema de coordenadas, pero en
el sistema de coordenadas de campo orientado todas las variables del rotor han
sido eliminadas de la formulación. Reemplazando estas variables aparece el
módulo y dirección de la corriente de magnetización im y δ respectivamente. Aun
cuando estas nuevas variables no son medibles directamente, están referidas al
sistema de coordenadas del estator, lo que simplifica en cierto modo el problema.
Sustituyendo las expresiones 3.90 y 3.91 en 4.51, se obtiene:
diq  ( M er )   di
dim 
p = R i + Lˆ  id d + iq
+
 δ iq im + id

'
dt 
Lr 
dt 
 dt
4.52
 di
di  ( M er )  dim 
q = δ Lˆ'eie2 + Lˆ'e  id q − iq d  +
 δ id im + iq

'
dt 
Lr 
dt 
 dt
4.53
ie2 = id2 + iq2
4.54
2
'
2
e e
'
e
'
2
donde:
Las ecuaciones 4.52 y 4.53, dependen de tres parámetros o combinación de
parámetros del modelo dinámico. También son función de dos tipos diferentes de
variables, unas que se pueden medir directamente en bornes de la máquina, y las
otras que es necesario estimar mediante el propio modelo. Las potencias activas y
reactivas instantáneas, así como la magnitud de la corriente del estator se obtienen
de las mediciones instantáneas de tensiones y corrientes en las bobinas. Las
corrientes id , iq , im y la posición δ así como sus respectivas derivadas tienen que
estimarse del modelo. Para resolver este problema es necesario determinar en
primer lugar la posición instantánea δ (t ) .
La posición angular del vector espacial de la corriente de magnetización
δ (t ) . se puede obtener de la información suministrada por el propio estimador de
estado del sistema de control. Sin embargo esta solución no es satisfactoria, debido
a que existen grados de libertad suficientes en las ecuaciones 4.53 y 4.54, para
obtener un conjunto de parámetros dependientes de este ángulo. Este conjunto de
parámetros cumple con las ecuaciones de potencia instantánea pero puede no
representar el comportamiento dinámico del convertidor. Este razonamiento
- 29 -
sugiere la necesidad de conocer de la información más o menos precisa de algún
parámetro del modelo.
Los métodos de estimación paramétrica que reducen las variables no
medibles por derivación de las ecuaciones originales, necesitan definir una relación
adicional entre las inductancias, para identificar el resto de los parámetros. Una de
las relaciones utilizadas con mayor frecuencia consiste en definir que las
reactancias de fuga del estor y rotor son iguales [6]. Otra posibilidad puede ser
indicar que las bobinas del rotor no tienen fuga, en este caso la dispersión queda
concentrada completamente en los devanados estatóricos. Esta última hipótesis,
más o menos discutible, puede simplicar el proceso de estimación de la dirección
de la referencia de campo orientado. En la figura 4.5 se presenta el circuito
equivalente transitorio de una máquina de inducción en coordenadas primitivas δ = 0; δÝ= 0 -, con la inductancia del rotor L'r , igual a la inductancia mutua estator
rotor M er' .
L'e − M er'
Re
Rr
i re
ie
ve
im
M 'er
jθÝM 'er i m
+
Fig. 4.5 Circuito equivalente transitorio de la máquina de inducción en
coordenadas primitivas sin reactancia de fuga en el rotor
En estas condiciones la corriente de magnetización i m , del circuito
equivalente en coordenadas primitivas, coincide con la corriente de magnetización
utilizada como referencia en el sistema de coordenadas de campo orientado. La
determinación de la dirección de este vector puede realizarse integrando la
ecuación de la malla estatórica:
- 30 -
v e = Re i e + Lˆe
di e
di
+ M er' m ⇒
dt
dt
4.55
t
'
jδ
∫ ( ve − Rei e ) dτ − Lˆei e = M er i m = λme = λmr + j λmi
o
De la expresión 4.55, se obtiene directamente las funciones trigonométricas
de la dirección δ :
t
λm = ∫ ( ve − Reie ) dτ − Lˆeie
r
r
r
4.56
r
o
t
λm = ∫ ( ve − Reieα ) dτ − Lˆeieα
i
4.57
i
o
λm =
cosδ =
(λ ) + (λ )
2
2
mr
4.58
mi
λm
λm
λm
; senδ =
; tan δ =
λm
λm
λm
r
i
4.59
r
i
La derivada de la posición angular de la referencia de campo orientado δ ,
se puede obtener a partir de la expresión 4.55:
di
di
v e = Re i e + Lˆe e + M er' m ⇒
dt
dt
d λm  d λm
 e jδ = ( v + jv ) − R ( i + ji ) − Lˆ  dir
=
+ jδλ
m
r
i
e r
i
e
dt
 dt

 dt


di 
di
λmr  vi − Reii − Lˆe i  − λmi  vr − Reir − Lˆe r
dt 
dt


δ =
2
2
( λmr ) + ( λmi )
+j
dii
dt

⇒

4.60



En estado cuasi-estacionario, la velocidad angular del rotor θ , y la corriente
de magnetización im , son prácticamente constantes. Al introducir estas hipótesis
simplificativas en las ecuaciones de potencia activa y reactiva instantánea 4.52 y
4.53, se obtiene el sistema siguiente:
- 31 -
diq
2
di
ie
id . d + iq .

 p
dt
dt
q = 
diq
did
  
2
 0 δ ie + id . dt − iq . dt

δ id .iq   Re 


  Lˆe 

δ id2   M er' 

4.61
donde:
id  cos δ − senδ  ir 
i  = 
 
 q   senδ cos δ   ii 
 pid  cos δ − senδ   pir   senδ
 pi  = 
   + δ  cos δ

 q   senδ cos δ   pii 
cos δ  ir 
senδ   ii 
4.62
Con un mínimo de dos mediciones linealmente independientes, es posible
determinar los parámetros de la máquina de inducción mediante las técnicas de
regresión lineal. La constante de tiempo del rotor se obtiene directamente
evaluando la ecuación 3.93, en las condiciones de operación cuasi-estáticas:
i
i
1
1
Tr = q ≈ q 4.63
im (δ − θ ) id (δ − θ )
Esta técnica de estimación paramétrica requiere cierta precisión en la
medida de la inductancia de dispersión de la máquina. Este parámetro tiene la
ventaja de ser poco dependiente de la temperatura y de la saturación, por esta
razón es recomendable realizar ensayos de rotor bloqueado o utilizar los datos
nominales de la máquina para su determinación. Los errores en esta evaluación no
interfieren en el comportamiento del modelo en régimen permanente, pero sí en
régimen transitorio.
Un método alterno al propuesto, consiste en considerar al menos dos
instantes durante la operación en régimen permanente pero con velocidad
diferente. La técnica más simple es la que utiliza como uno de estos puntos el
correspondiente a la condición de vacío. En vacío la corriente iq es nula, y toda la
magnitud de la corriente ie , inyectada en el estator de la máquina es igual a la
componente directa id . En la operación de régimen permanente las derivadas de
las corrientes id e iq , son nulas. De esta forma se obtiene de la expresión 4.61, las
siguientes relaciones:
- 32 -
q = δ L'eie2
⇒
(
)
p = Re − δ M er' ie2
L'e =
q
q
=
2
ω eie ω mie2
4.64
R i2 − p
M = ee 2
ω eie
⇒
'
er
Despreciando la resistencia del estator, o utilizando el valor medido
directamente en bornes de la máquina, se pueden estimar con precisión los otros
parámetros. Con una medida realizada en una condición de carga, que mantenga
la misma densidad de flujo en el entrehierro - relación tensión-frecuencia constante
-, se puede obtener la constante de tiempo del rotor de la expresión 4.63. En este
caso la corriente del eje directo coincide con la magnitud de la corriente del estator
de la medida instantánea realizada en la condición de vacío.
El método anterior es muy simple pero tiene un inconveniente importante,
en la mayoría de las aplicaciones prácticas es imposible obtener el punto de
operación en vacio. Incluso cuando esto es posible, las propias pérdidas mecánicas
de la máquina, hacen imposible el empleo de este método. Sin embargo, una
extensión del mismo es posible cuando se consideran dos puntos de operación en
régimen permanente, pero manteniendo la hipótesis de igualdad de flujos en el
entrehierro. Para mantener esta hipótesis es necesario realizar los ensayos en dos
condiciones de operación a diferente velocidad, pero con una relación de tensiónfrecuencia prácticamente constante. Con estas consideraciones se puede obtener
directamente la inductancia Lˆ e a partir de la ecuación 4.53, correspondiente a la
potencia reactiva instantánea inyectada en el estator de la máquina:
2

M er' )
(
2
2
 q1 = δ1 Lˆeie1 + δ1id
L'r
q1 − δ1 Lˆeie21 δ1

⇒
=

Lˆ i 2 δ2
' 2
δ
−
q
2
2 e e2

M er )
2
2 (
q2 = δ2 Lˆeie 2 + δ2id
'
Lr

δ q − δ q
⇒ Lˆe = 1 2 2 2 21
δ δ ( i − i )
1 2
e2
e1
4.65
De las ecuaciones 4.52 y 4.53 se puede encontrar la relación siguiente para el
2
M'
parámetro ( er ) ' :
Lr
(M )
' 2
er
L'r
p − Reie2 )
(
1
= 2 1+
2
δ ie
q − δ Lˆeie2
2
(
- 33 -
)
4.66
El único parámetro desconocido en la expresión 4.66, es la resistencia del estator
R e . Si se desprecia esta resistencia en una condición de operación cercana al punto
de carga nominal de la máquina, o se realiza una medida directa del parámetro, se
puede obtener la relación existente entre el cuadrado de la inductancia mutua
estator-rotor y la inductancia propia del rotor. Este parámetro determina el
coeficiente independiente de la ecuación del par eléctrico.
El procedimiento descrito anteriormente tiene una relación muy estrecha
con el diagrama de círculo del circuito equivalente de la máquina de inducción. Se
debe recordar que es suficiente con la información completa de dos puntos de este
diagrama, para trazar y calibrar todo el diagrama de círculo. Esta situación es
análoga al conocimiento de todos los parámetros del circuito equivalente. El
principal problema de este procedimiento de estimación consiste en la necesidad
de mantener condiciones de régimen permanente antes de proceder a realizar las
medidas correspondientes. Cuando se considera que la variabilidad de los
parámetros de la máquina es mayor en varios órdenes de magnitud con respecto a
las constantes de tiempo eléctricas y mecánicas, el método es de gran interés
práctico. El otro inconveniente en la aplicación de esta técnica reside en la
necesidad de mantener prácticamente constante la corriente de campo durante los
dos ensayos o medidas. Esta limitación no es demasiado rigurosa, debido a que
durante la operación en régimen permanente es aconsejable mantener la mayor
corriente de campo posible para producir el máximo de par eléctrico con las
menores corrientes de armadura. Las fuentes electrónicas actuales son capaces de
realizar este control con mucha sencillez.
La constante de tiempo del rotor T r , se obtiene a partir de la misma
expresión 4.63, pero despejando de las ecuaciones 4.52 y 4.53, la relación entre las
corrientes directa y cuadratura:
Tr =
iq
id
⋅
( p − Reie2 ) ⋅ 1
1
=
(δ − θ)
q − δ Lˆeie2 (δ − θ)
(
)
4.67
A continuación se presentan los resultados obtenidos de la aplicación del
método propuesto de estimación paramétrica basado en la formulación de
potencias activas y reactivas instantáneas:
- 34 -
Aplicando al modelo transitorio de la máquina de inducción en
coordenadas de campo orientado a un sistema de tensiones trifásicas sinusoidales
de frecuencia fundamental, balanceado, y de secuencia positiva, con tres
condiciones de carga diferentes, se obtienen los siguientes registros para el
régimen permanente en el sistema adimensional de unidades:
ωm
ve
ie
im
δ
δÝ
376.9
0.9757
349.6618
1.0
0.9744
0.4614
726.6561
1.0
1130.9
1.0
0.4976
-j0.9301
0.5415
-j0.9566
-0.2372
-j0.4160
0.4624
753.9
1.4913
-j0.8809
1.4991
-j0.8677
1.4913
-j0.8809
0.4789
1179.1497
1.0
Tiempo
[pu]
Utilizando el método de estimación paramétrica propuesto, con los datos
correspondientes a la primera y segunda fila de la tabla anterior, se obtiene los
siguientes resultados:
Parámetro
Re
L'e
Estimación [p.u.]
Exacto [p.u.]
Error ( % )
0.0663
0.0552
-16.74
3.1055
3.6166
16.46
(L ) / L
3.0313
3.4214
12.87
Tr
69.6754
82.4472
18.33
2
'
er
'
r
Si se utilizan los datos correspondientes a la segunda y tercera fila, con lo
cual se incluye el punto de operación en vacío, se obtienen los siguientes
parámetros:
Parámetro
Re
'
Le
Estimación [p.u.]
Exacto [p.u.]
Error ( % )
0.0552
0.0552
0
3.6165
3.6166
0
(L ) / L
3.4210
3.4214
0.01
Tr
84.3895
82.4472
- 2.3
2
'
er
'
r
Se puede observar que el error de la primera estimación es inferior al 18.5%.
Este error se puede reducir a menos del 2.3%, cuando se utiliza la información del
punto de vacío de la máquina de inducción para la estimación de la resistencia e
inductancia de estator. Además, la inclusión del punto de operación en vacío
elimina la necesidad de mantener constante la corriente de magnetización durante
- 35 -
los ensayos. El error de la estimación del primer caso se debe fundamentalmente a
la diferencia existente entre las corrientes de magnetización de los dos puntos de
operación, los controladores vectoriales pueden mantener esta corriente
prácticamente constante y reducir apreciablemente el error de estimación. Los
controladores de velocidad que operan manteniendo constante la relación entre la
tensión y la frecuencia de alimentación de la máquina de inducción, también
mantienen esta corriente prácticamente constante.
La principal ventaja del método de estimación paramétrica propuesto es la
eliminación del cálculo de las derivadas de las variables de estado medibles. Sin
embargo, el procedimiento está restringido a que las medidas se realicen en puntos
de operación correspondientes al régimen permanente. Esta limitación no es
demasiado severa debido a que los parámetros de la máquina cambian lentamente
en comparación con la dinámica del controlador de velocidad. Hay que recordar
que el efecto pelicular tiene escasa importancia en los controladores vectoriales
debido a que operan con deslizamientos cercanos a los valores nominales en todo
el rango de velocidad, y a que el cambio de temperatura en el interior de la
máquina es comparativamente lento. La saturación si hace cambiar más
rápidamente los parámetros.
4.5
Estimación del estado de la máquina de inducción para el control del par, la
velocidad o la posición de accionamientos electromecánicos.
En las secciones anteriores se han revisado y propuesto diversas técnicas
orientadas a la determinación de los parámetros de los circuitos equivalentes de la
máquina de inducción. Algunos de estos procedimientos pueden ser realizados en
tiempo real con las herramientas de cálculo que existen en la actualidad. La
estimación paramétrica en tiempo real tiene por objeto corregir las desviaciones del
modelo, ocasionadas por la variabilidad de los parámetros durante la operación
del convertidor. La variación de los parámetros del modelo durante la operación
impiden la determinación precisa del estado del sistema. Si no se conoce el estado
de las variables del modelo, se complica notablemente las acciones de control
necesarias sobre las fuentes para regular el comportamiento estático y dinámico de
la máquina de inducción.
El objetivo fundamental de la estimación de estado en la máquina de
inducción se centra en la determinación de las variables internas no medibles, que
- 36 -
en definitiva, producen el par eléctrico, y por lo tanto, la velocidad del
accionamiento.
Las transformaciones de coordenadas realizadas sobre las
ecuaciones primitivas de la máquina permiten desacoplar la producción del par
eléctrico en dos variables que pueden ser controladas independientemente. Esta
idea, completamente análoga al principio de funcionamiento y control de las
máquinas de corriente continua con excitación independiente, ofrece alternativas
interesantes para el desarrollo de accionamientos rápidos de la máquina de
inducción. La necesidad de la estimación de estado aparece cuando se calculan las
referencias que deben seguir las fuentes de alimentación controlables. Estas
fuentes deben ser capaces de excitar a la máquina con los valores adecuados para
obtener la salida deseada en cada instante de tiempo.
La alternativa que se ofrece a la necesidad de estimar el estado de las
variables internas y no medibles del convertidor es la introducción de sensores y
complejos dispositivos en el sistema, capaces de medir la dirección y la magnitud
del flujo resultante en el entrehierro o el par eléctrico instantáneo. Las condiciones
de operación reales dificultan, o incluso imposibilitan, la aplicación de este tipo de
equipamientos. Las técnicas de estimación de estado ofrecen una alternativa
menos costosa a este problema, además es totalmente factible su implantación en
condiciones reales de operación, y en sistemas industriales de diversa índole.
La estimación del estado de las variables del modelo equivalente de la
máquina de inducción es un problema directo y determinístico, a diferencia del
problema de la estimación paramétrica, que se plantea la mayoría de las veces
como un problema de regresión u optimización no lineal. En la estimación de
estado se utiliza la información medible o disponible en los ejes eléctricos y
mecánicos de la máquina, para obtener las variables necesarias por el controlador
de par, velocidad o posición del accionamiento electromecánico. Esta información
se obtiene normalmente mediante un proceso de integración de las ecuaciones
diferenciales que definen el modelo de la máquina, considerando que las variables
medidas determinan, o pueden determinar después de cierto procesamiento de las
señales, las condiciones iniciales del problema.
Tal vez el estimador de estado más simple puede estar constituido por el
circuito equivalente clásico. Si se miden las tensiones y corrientes instantáneas en
bornes del estator de la máquina de inducción, se pueden calcular las potencias
activas y reactivas instantáneas. El valor medio de estas variables puede ser
- 37 -
procesado para determinar los valores fasoriales de las corrientes inyectadas en el
estator. Con el fasor de la corriente del estator, se calcula la caída de tensión en la
reactancia de dispersión y en la resistencia de las bobinas. Restando la caída en
esta impedancia de la tensión aplicada en el estator, se obtiene el fasor de la fuerza
electromotriz en la rama de magnetización. Con esta variable se calcula el fasor
correspondiente a la corriente de magnetización. Restando la corriente de
magnetización de la corriente inyectada en el estator, se obtiene la corriente del
rotor referida al estator. Con la corriente del rotor se puede calcular directamente
el par eléctrico en el eje, siempre y cuando se conozca el deslizamiento relativo de
la máquina. Para calcular el deslizamiento relativo es necesario conocer la
frecuencia de las fuentes de alimentación, la velocida del eje mecánico y el número
de pares de polos del convertidor electromecánico. En resumen:
•
Cálculo de las potencias instantáneas y medias:
T

1
 P = p (t ) = ∫ p (τ )dτ = p
 p (t ) = va ia + vb ib + vc ic
T 0


⇒
1

T
q (t ) = 3 ( vbc ia + vca ib + vabic )  Q = q(t ) = 1 q(τ )dτ = q


T ∫0

•
4.68
Cálculo de los fasores de la tensión y corriente del estator:

2
2
ie = iα + iβ =


v = v 2 + v 2 =
α
β
 e

(
3
(
2 ia
3
) (
2
v
2 a
+
2ia +
) +(
2
3
2va +
2 ib
3
)
2
T
⇒ I e = ie (t ) =
v
2 b
)

Q
−1 
φe = tan   = cos

P

−1
Ie = Ie ⋅ e
Q
− j tan −1  
 P
2
1
ie (τ )dτ = ie
T ∫0
T
1
⇒ Ve = ve (t ) = ∫ ve (τ )dτ = ve
T 0
i 

Ie 

3
2 a
= Ie ⋅ e

− j cos−1 


4.69
4.70
3
2 ia
Ie




4.71
Ve = Ve ⋅ e = Ve
j0
•
Fuerza electromotriz de la rama de magnetización:
- 38 -
Ee = Ve − ( Re + jX σ e ) .I e = Ve − Z e .I e ⋅ e
•

X 
 Q 
j  tan −1  σ e  − tan −1   
R
 P  

e


Corriente de la rama de magnetización:
 1
1 
I m = Ee 
−j

Xm 
 Rm
•
4.73
Corriente del rotor referida al estator:
Ir = Ie − Im = Ie ⋅ e
•
4.72
Q
− j tan −1  
P
 1
1 
− Ee 
−j

Xm 
 Rm
4.74
Par eléctrico:
Te =
1
ωe
⋅ ( Ir ) ⋅
2
Rr
Rr
=
⋅ I r ⋅ I*r
s (ω e − ω m )
4.75
La expresión 4.75, determina el par eléctrico de una máquina de inducción
que se encuentra operando en régimen permanente equilibrado, excitada mediante
una fuente de tensión sinusoidal de secuencia positiva. El inconveniente de este
proceso de estimación es la pérdida de precisión durante el régimen dinámico y
desequilibrado. Además, las fuentes de excitación de la máquina no son
necesariamente sinusoidales. Otro problema que presentan estos estimadores para
su aplicación en tiempo real es el retardo de tiempo necesario para realizar la
integración que determina los valores medios o efectivos de las potencias,
tensiones y corrientes instantáneas. Sin embargo, cuando las medidas se realizan
en condiciones de operación equilibradas y de régimen permanente, la necesidad
de este retardo desaparece.
Para obtener un estimador de estado que reproduzca el comportamiento
dinámico de las variables de la máquina, es indispensable utilizar como base el
modelo de la máquina de inducción en ecuaciones diferenciales. Una de las ideas
más utilizadas consiste en utilizar las ecuaciones en coordenadas de campo
orientado para realizar el proceso de estimación del estado de las principales
variables internas del convertidor.
Esto se debe, como ya se mencionó
anteriormente, al desacoplamiento existente entre las variables productoras del par
eléctrico. Los estimadores de estado basados en las ecuaciones de campo
orientado se utilizan para reproducir en laa máquinas de inducción, las técnicas de
- 39 -
control de velocidad, posición o par empleadas en las máquinas de corriente
continua con diferentes esquemas de excitación [7,26,41,71].
El estimador de estado más simple posiblemente es el esquema que utiliza
la corriente del estator como fuente independiente. Si el estator de la máquina de
inducción se alimenta mediante una fuente de corriente independiente, las dos
ecuaciones de tensión correspondientes a este sistema no son necesarias para la
representación del comportamiento dinámico del convertidor. Las ecuaciones de
tensión del estator son en este caso, simples ecuaciones de salida que determinan la
tensión necesaria en bornes de la máquina para satisfacer la inyección de corriente
que se define independientemente. Las dos ecuaciones de tensión restantes,
correspondientes al modelo del rotor, y la ecuación dinámica, determinan el
comportamiento eléctrico y mecánico de la máquina en estas condiciones de
alimentación. El principal problema que se presenta en este esquema de
estimación de estado es la dependencia extrema de las variables internas del
modelo con los parámetros respectivos. Esto se debe fundamentalmente a que las
transformaciones de coordenadas requieren información precisa de la posición
exacta del vector espacial de la corriente de magnetización modificada. Esta
posición solamente puede ser determinada con la precisión que se obtiene de los
estimadores paramétricos. En todos los estimadores de estado, existe una
dependencia importante de las variables del modelo con los parámetros, pero en
este esquema, la dependencia es mayor debido a que las variaciones o desviaciones
de los parámetros afectan el propio sistema de referencia. A continuación se
describe el proceso básico de estimación de estado del modelo en coordenadas de
campo orientado, con inyección de corrientes independientes en el estator [53,75]:
•
Ecuación del campo:
i −i
pim = d m
Tr
•
⇒
tn+1
∫ [i (τ ) − i
d
m
(τ ) ] dτ
4.76
iq (τ ) 
 dτ
Tr ⋅ im (τ ) 
4.77
tn
Ecuación de la posición del campo:
pδ = ω m +
•
1
im (tn +1 ) =
Tr
iq
Tr ⋅ im
⇒
δ (tn +1 ) =
tn+1
tn
Variables de salida del estimador:
- 40 -

∫ ω
m
(τ ) +
Te
(M )
=
' 2
er
L'r
⋅ im ⋅ iq
vd = Reid + Lˆe pid − Lˆe δ ⋅ iq
vq = Reiq + Lˆe piq + Lˆe δ ⋅ id
4.78
(M )
+
' 2
er
pim
4.79
δ ⋅ im
4.80
L'r
(M )
+
' 2
er
L'r
Para determinar las corrientes o las tensiones del estator, se utilizan las dos
transformaciones de coordenadas siguientes:
•
Transformaciones entre las coordenadas de campo orientado dq y las
coordenadas ortogonales αβ :
xd + j xq = ( xα + j xβ ) ⋅ e − jδ ⇒
 xd   cos δ
x  = 
 q   − sen δ
•
sen δ   xα   xα   cos δ
   =
cos δ   xβ   xβ  sen δ
− sen δ   xd 
 
cos δ   xq 
4.81
Transformaciones entre las coordenadas ortogonales αβ y las
coordenadas primitivas abc:
2
j 2π
1 e 3
x≡
3
 2
 xα   3
x  = 
 β  0


−
1
6
1
2
e
j 43π
 xa 
  xb  = xα + j xβ
 
 xc 

1  x
 a 
6  x  = 
b
1   

x
−
  c  
2

−
 2

3
 xa  
 x  = − 2
 b  3
 xc  

 0

3
2
2
2

0 

1   xα 
 
2   xβ 
1 
−

2 
- 41 -

0 
x
  a 
  xb 
2

4.82
La transformación 4.82, convierte las variables primitivas a coordenadas
ortogonales. Si se miden dos de las tres corrientes del estator, se obtienen
directamente las corrientes en este sistema de coordenadas. Esta primera
transformación es independiente de los parámetros del modelo. Las corrientes en
coordenadas ortogonales αβ se transforman a coordenadas de campo orientado
mediante la expresión 4.81. En este caso la transformación depende de la posición
angular δ . Esta variable depende del valor de la constante de tiempo del rotor T r .
Cualquier error en el valor de este coeficiente se traduce en un error acumulado a
través del tiempo de la posición angular δ . Si esta variable no coincide con la
posición real del flujo en la máquina, la transformación 4.81, no desacopla las
variables productoras del par eléctrico. En la figura 4.6, se presenta el diagrama de
control correspondiente a este tipo de estimador de estado. El desarrollo de estos
esquemas se puede realizar mediante circuitos analógicos o digitales. En la
actualidad es muy frecuente incorporar todo el procesamiento de señales dentro
del computador o controlador programable que dirige el proceso [26,41].
cos δ
ib
2
x
iq
+
x
ia
Transformación
abc - αβ
iα
L'r
1
Tr
x
x
M 'e r
im
x
2
2
+
+
id
Te
2
-
+
3
2
δ
sen δ
iβ
+
δ
ωr
1
Tr p +1
Transformación
αβ - dq
÷
im
+
iq
+
1
p
δ
Tr im
Ecuaciones de campo orientado
Fig. 4.6 Estimador de estado de las variables del modelo de una máquina de
inducción en coordenadas de campo orientado con excitación de corrientes
independientes en el estator
La estimación de estado por campo orientado requiere la adaptar de los
parámetros del modelo a medida que transcurre el proceso. Para el control
adpativo del proceso se utilizan dos técnicas básicas: la estimación paramétrica en
tiempo real, y la adaptación de parámetros hasta cumplir con una consigna. La
- 42 -
estimación paramétrica se ha discutido en las secciones anteriores de este capítulo.
La adaptación de parámetros se fundamenta en las técnicas clásicas del control
adaptivo o adaptativo. El control adaptivo corrige los parámetros del controlador,
hasta que se cumplan ciertas condiciones que garanticen la precisión del sistema.
En los controladores por campo orientado se pueden utilizar varias consignas para
cumplir con esta finalidad. En ocasiones se pueden realizar comparaciones con las
potencias activas o reactivas. En algunos casos se intenta obtener un punto de
operación determinado, por ejemplo corriente mínima. Si el parámetro que se está
ajustando o adaptando no reproduce el comportamiento de la máquina, será
posible acercarse al punto establecido variando apropiadamente este coeficiente.
Tradicionalmente este tipo de procesamiento se realiza en un régimen permanente
o prácticamente permanente.
Otra posibilidad consiste en utilizar estimadores de estado en coordenadas
de campo orientado con excitación de tensión independiente en el estator. Estos
estimadores tienen la ventaja de ser aplicables directamente con fuentes
tradicionales de tensión cuya amplitud y frecuencia es regulable. El principal
problema reside en el incremento de los cálculos necesarios para resolver las
ecuaciones diferenciales del estator de la máquina de inducción, y los tiempos que
estos cálculos requieren. En este caso, las ecuaciones 4.79 y 4.80, no son de salida,
es necesario integrarlas para determinar las corrientes de los ejes directo y
cuadratura respectivamente. Una vez obtenidas estas corrientes, se utiliza el
mismo estimador de estado con inyección de corrientes independientes ilustrado
en la figura 4.6. Las corrientes directa y cuadratura se obtiene de la siguiente
forma:
•
Corrientes del estator en coordenadas de campo orientado:
pi d =
1

v d − Re + R r


ˆ
Le 
( )
M 'er
2
L'r

1

piq = vq −  Re + Rr
ˆ
Le 


i + R
r
 d
( )
'
M er
L'r
2
( )
M 'er
L'r
2
i 2q 
 

i m  +  ω mi q +
 
T r ⋅ im 
2
  i ⋅i 
M er' )
(

q d

i
i
ω
−
q

m m −
'
  Tr ⋅ im 
Lr


4.83
4.84
Integrando las ecuaciones 4.83 y 4.84, se obtienen las corrientes del estator
en coordenadas de campo orientado, en función de las variables de estado del
sistema - velocidad angular mecánica, corriente de magnetización y corrientes del
- 43 -
estator -, y de las fuentes de tensión independientes. Las transformaciones de
coordenadas necesarias son las mismas que en el caso anterior pero aplicadas sobre
las tensiones en lugar de las corrientes.
Para resolver el problema de la dependencia de los resultados del estimador
de estado, con la precisión o variabilidad de los parámetros del modelo, se pueden
utilizar sistemas de coordenadas en los cuales la referencia se define
independientemente de estos valores. El sistema de coordenadas arbitrarias
analizado en la sección 3.7, cumple con esta condición. Los resultados que se
obtienen a partir de este modelo dependen de la precisión con la que se
determinan los parámetros, pero pequeños errores en estas estimaciones no
determinan variaciones significativas en el valor instantáneo de las variables de
estado. De las expresiones 3.86 y 3.87, se pueden obtener las siguientes derivadas
de las corrientes del modelo en coordenadas arbitrarias:
 vδeˆ   Re + jδˆ L'e
 ˆ = 
 vδr   j (δˆ − θ) M er'
  iδˆ   L'
jδˆ M er'
e
 e +
ˆ '   iδˆ   M er'
Rr + j (δ − θ ) Lr   r 
ˆ
δ
M er'   pi e   vδe 
= 

L'e   piδrˆ   0 
ˆ
⇒
 piδeˆ   L'e
 ˆ =  '
 piδr   M er
M er' 

L'e 
−1
  δˆ   R + jδˆ L'
 ve
e
e
  −    0   j (δˆ − θ) M er'
4.85
 iδˆ  
jδˆ M er'
  e 
ˆ '  iδˆ  
Rr + j (δ − θ ) Lr   r  
La integración numérica de las ecuaciones diferenciales 4.85, se acelera
cuando se define una referencia que gire a una velocidad cercana a la de los
vectores espaciales. Este modelo utiliza como fuente independiente el vector
espacial de la tensión del estator. Utilizar este vector, o en su lugar la velocidad
angular mecánica del rotor, reduce el tiempo y los cálculos necesarios para la
evaluación numérica del estimador.
Una vez calculados los valores instantáneos de las variables de estado en el
sistema de coordenadas arbitrarias, es muy simple transformar la solución al
sistema de coordenadas de campo orientado. Para esto se obtienen los vectores
espaciales en el sistema de coordenadas del estator y posteriormente se determina
la dirección δ , y la magnitud im , del vector espacial de la corriente de
magnetización modificada:
- 44 -
j (δˆ +ξ )
L'r e
L'r δˆ 
ˆ
jδˆ  δˆ
i = i + ' i r = e i e + ' i r  = e jδ im e jξ = im e
= im e jδ
M er
M er 

e
m
e
e
4.86
Utilizando las transformaciones a coordenadas de campo orientado 4.81, se
pueden obtener resultados más precisos por este estimador. Las razones
fundamentales para este incremento de la precisión en los resultados del estimador
arbitrario consiste en la independencia de la transformación con los parámetros y
en la formulación del problema con dos ecuaciones complejas, equivalentes a
cuatro ecuaciones diferenciales reales. La principal desventaja de esta alternativa
reside en la necesidad de una mayor cantidad de cálculo para resolver las
ecuaciones diferenciales del estimador de estado, y también para realizar las
transformaciones de las variables arbitrarias a las variables de campo orientado
que utilizan los controladores de par, velocidad o posición de la máquina de
inducción.
4.5
Controladores vectoriales de la máquina de inducción con sistemas
integrados de estimación paramétrica y estimación de estado.
En las secciones anteriores de este capítulo se han discutido y evaluado
varias alternativas para la estimación de los parámetros del modelo de la máquina
de inducción, y las principales ideas aplicables al empleo de estos modelos en la
estimación de estado que requieren los controladores rápidos de par, velocidad o
posición. Cuando se requiere obtener la respuesta rápida de un accionamiento
determinado, es necesario conocer con la mayor precisión posible las relaciones
entre las diferentes variables del proceso y sus valores en cada instante de tiempo.
En la figura 4.7, se presenta el diagrama esquemático de un sistema de control con
estas características.
- 45 -
[v abc ], [i abc ], ω m
Estimador
de Estado
[k], Tr
Estimador
Paramétrico
[v abc ],[i abc ]
δ, ω s , i d ,i q
ωm
Te , i m , δ
ωref
Controlador
Inversor
[i ref ]
Mot.
Ind.
ωm
Fig. 4.7 Control vectorial adaptivo de la máquina de inducción
El control vectorial adaptivo de la figura 4.7, puede regular la velocidad, la
posición o el par de la máquina de inducción. Para este fin se alimenta mediante
un inversor trifásico que inyecta las corrientes en cada una de las ramas, siguiendo
a una consigna calculada por el bloque controlador. El controlador del proceso, se
realimenta con información de la máquina obtenida del estimador de estado y de
medidas directas. En el controlador se realizan las acciones de comparación entre
los valores deseados o referencias y las magnitudes medidas o estimadas. Después
se realizan acciones de control proporcional, integral e incluso derivativo en
algunos casos, que definen las corrientes de referencia para el inversor. La
estimación del estado de las variables no medibles se puede obtener mediante
alguno de los métodos analizados en la sección anterior. Cuando la precisión del
estimador de estado depende fuertemente de los parámetros de la máquina, tal
como sucede en el caso particular de los estimadores basados en los modelos de
campo orientado, es necesario utilizar un estimador paramétrico en tiempo real
que corrige las variaciones de los parámetros del modelo, en función de las
variables medibles del convertidor. El estimador de estado y el estimador
paramétrico intercambian información para cumplir su función.
En la figura 4.8, se ha esquematizado la estructura básica de un controlador
de velocidad que genera las consignas de corriente a un inversor con modulación
delta de la corriente. Este controlador reproduce las funciones básicas del control
clásico de las máquinas de corriente continua. La referencia de velocidad angular
se compara con la velocidad angular mecánica. El error entre estas dos señales se
- 46 -
introduce en un controlador proporcional integral, que lo convierte en una
consigna de par eléctrico. El par eléctrico de referencia se compara con el par
eléctrico obtenido a partir del estimador de estado. El error entre el par eléctrico
estimado y el par eléctrico de referencia se introduce en un segundo controlador
proporcional integral que determina la consigna de la corriente de referencia
correspondiente al eje cuadratura. Simultáneamente, el valor de la velocidad
mecánica se pasa por un bloque funcional que determina el valor más conveniente
de la corriente de magnetización para un punto de operación determinado. Si la
velocidad angular mecánica es menor que su valor nominal, la referencia de la
corriente de magnetización se mantiene constante en su valor nominal, que
corresponde a la condición de flujo nominal. Por otra parte, si la velocidad es
superior al valor nominal, se debilita la corriente de magnetización para no exceder
la potencia nominal del convertidor.
La consigna final de corriente de
magnetización se compara con la corriente de magnetización obtenida nuevamente
del estimador de estado, el error se introduce en un tercer controlador
proporcional integral que produce la consigna de corriente correspondiente al eje
directo. Las dos consignas de la corriente se transforman del sistema de
coordenadas de campo orientado dq , al sistema de coordenadas ortogonales αβ , y
posteriormente al sistema de coordenadas primitivas abc. Finalmente, se obtienen
las referencias de las corrientes de fase que debe suplir el inversor.
T e est.
controlador
de
velocidad
ωref
+
k
k + p2
1
-
controlador
de
torque
-
k
k + p4
3
+
sen δ est.
i q ref.
x
im
2
3
x
+
controlador
de flujo
i m ref.
+
-
ωm med.
i a ref.
i α ref.
+
T e ref.
ωm
-
k
k + p6
5
x
1
+
i β ref.
2
+
x
i c ref.
i d ref.
-1
cos δ est.
i m est.
Fig. 4.8 Controlador de velocidad de la máquina de inducción
- 47 -
ib ref.
- 48 -