SOLUCION EXAMEN PRIMER PARCIAL MAT-101

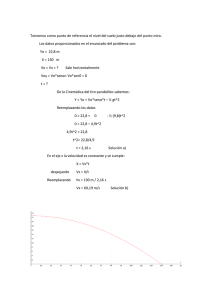
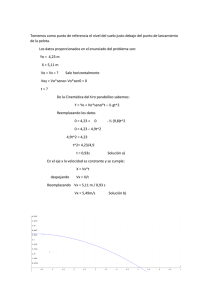
SOLUCION EXAMEN PRIMER PARCIAL MAT-101
1.- Hallar las coordenadas de los vértices de un triángulo sabiendo que las coordenadas de los puntos
A 1,1 ; B  3,6  y C  1,3
medios de sus lados son:
Solución.

 
 
Las coordenadas de los vértices son: D d x , d y ; E ex , ey ; F f x , f y

Por el punto medio se tiene:
d x  ex
2
dx  fx
bx 
2
e  fx
ax  x
2
cx 
Reemplazando
2cx  d x  ex

2  1  d x  ex

 2  d x  ex

2bx  d x  f x

2  3  d x  f x

6  dx  fx

2ax  ex  f x

2 1  ex  f x
I 
6  2  ex  f x
Resolviendo

 III 
8  ex  f x 

2  ex  f x 

2  ex  f x
I 
 II 
 III 
en  II 

y
 IV 
8  ex  f x
 IV 

10  2 f x

fx  5
Pág. 1 de 12
LIMBERT AYZACAYO CHOQUE
f x en  II  :
Reemplazando
6  dx  f x

Reemplazando
d x en  I  :
2  d x  ex

6  dx  5

dx  1
 2  1  ex

Resolviendo análogamente se tiene:
dy  8
Las coordenadas de los vértices son:
D 1,8 ;
ex  3

ey  2
E  3, 2 
;

fy  4
F  5, 4 
Respuesta.
2.- Un arco tiene forma de semielipse con una luz de 15m , siendo su máxima altura de 5m . Hallar la
longitud de dos soportes verticales situados cada uno de tal forma que dividen en 3 la luz total.
Solución.
Del gráfico se tiene:
a  7.5
b5
Reemplazando en la ecuación:
x2
y2

1
7.52 52
Reemplazando
x2 y 2

1
a 2 b2


x2 
y  5 1  2 
 7.5 
2
I 
x  2.5 en la ecuación  I 
2

5 

   10
2
y  52  1    2  
2
  15   3
   
 2 
La longitud de los soportes es: y 
10
2  4.71 m
3
Respuesta.
Pág. 2 de 12
LIMBERT AYZACAYO CHOQUE
3.- Resolver:
a)
x 1
x

2 x 3 x
b)
3x  1
 4x  2
2x 1
Solución.
x 1
x

2 x 3 x
x 1
x


2 x 3 x
a)
x2  4 x  3  2 x  x2
0
 2  x  3  x 
x 1
x

0
2 x 3 x
 x  1 3  x   x  2  x   0
 2  x  3  x 

2x2  2x  3
0
 2  x  3  x 

La ecuación: 2 x  2 x  3  0 tiene no tiene raíces reales.
2
3 x  0
2 x  0


x1  3
x2  2
Ubicando los puntos en una recta real:
Determinamos los intervalos del conjunto solución:
 x  5
2x2  2 x  3
0
 2  x  3  x 
2  5  2  5  3
2

 2   5   3   5 
0


43
0
14
Verdadero
x  0
2x2  2 x  3
0
 2  x  3  x 
2  0  2  0  3
2

 2   0 3   0
0

3
0
6
Falso
x  4
2x2  2 x  3
0
 2  x  3  x 
2  4  2  4  3
0
 2  4  3  4 
2



43
0
14
Verdadero
Gráficamente tenemos el conjunto solución:
El sector sombreado es el conjunto solución:
Cs : x  3 ; x  2
Respuesta
Pág. 3 de 12
LIMBERT AYZACAYO CHOQUE
b)
3x  1
 4x  2
2x 1
Solución.
  4x  2 
3x  1
 4x  2
2x 1
Resolviendo:  I1  :
 4x  2 
3x  1
 4x  2
2x 1
3x  1
2x 1
 4 x  2 2 x  1  3x  1  0 
2x 1
2
8 x  3x  3
0
2x 1
 4x  2 
3x  1
0
2x 1
8 x 2  3x  3
0
2x 1
8 x 2  3x  3  0
4 x  2 
xi 



3  32  4  8  3
2 8
8 x 2  2  3x  1
0
2x 1

105 3
  0.82
 x1  

16
16

 x  105  3  0.45
 2
16
16

2x 1  0

x3  
1
2
 x  1
8 x 2  3x  3
0
2x 1
 x  0.7
8 x 2  3x  3
0
2x 1
x  0
8 x 2  3x  3
0
2x 1
 x  0.5
8 x 2  3x  3
0
2x 1
8  1  3  1  3
0
2  1  1
2

Falso
8  0.7   3  0.7   3
0
2  0.7   1
2

8  0  3 0  3
0
2  0  1
Verdadero
2

8  0.5  3  0.5   3
0
2  0.5   1
False
2

Verdadero
Pág. 4 de 12
LIMBERT AYZACAYO CHOQUE
CsI1 :  0.82  x  0.5
Resolviendo:
 I2  :
3x  1
 4x  2  0
2x 1
3x  1  8 x 2  2
0
2x 1
8 x 2  3x  1  0
;
x  0.45
3x  1
 4x  2
2x 1
3x  1   2 x  1 4 x  2 

0
2x 1
8 x 2  3x  1
8 x 2  3x  1

0

0
2x 1
2x 1
 x  0.21
b  b 2  4ac   3   3  4  8  1 3  9  32 3  41
xi 



  1
2a
2 8
16
16
 x2  0.58
1
2x 1  0

x3    0.5
2
2
 x  1
8 x 2  3x  1
0
2x 1
 x  0.4
8 x 2  3x  1
0
2x 1
x  0
8 x 2  3x  1
0
2x 1
 x 1
8 x 2  3x  1
0
2x 1
8  1  3  1  1
0
2x 1
2

8  0.4   3  0.4   1
0
2  0.4   1
Falso
2


8  0  3 0 1
0
2 0  1

8 1  3 1  1
0
2 1  1
Verdadero
2
Falso
2
CsI 2 :  0.5  x  0.21
;
Verdadero
x  0.58
La solución final es la intersección de los dos:
CsI1  CsI 2
Pág. 5 de 12
LIMBERT AYZACAYO CHOQUE
Cs :
x  0.58
Respuesta
4.- Hallar la ecuación de la circunferencia que pasa por los siguientes 3 puntos
A  4,5 ; B  3, 2  ; C 1, 4 
Solución.
Reemplazando los puntos en la ecuación general de la circunferencia  I  :
x2  y 2  Dx  Ey  F  0
I 
Reemplazando A  4,5 
42  52  4D  5E  F  0

4D  5E  F  41
 II 
Reemplazando B  3, 2 
32   2   3D  2E  F  0
2

3D  2E  F  13
 III 

D  4E  F  17
 IV 
Reemplazando C 1, 4 
12   4   1D  4E  F  0
2
Resolviendo el sistema de ecuaciones:
4 D  5E  F  41
3D  2 E  F  13
D  4 E  F  17
 II  

 III  
 IV 
Resolviendo por Cramer:
Pág. 6 de 12
LIMBERT AYZACAYO CHOQUE
41
13
17
D
4
3
1
5 1
2 1
4 1 84

7
5 1
12
2 1
4 1
4
3
1
E
4
3
1
4 5
3 2
1 4
F
4 5
3 2
1 4
41
13
17
5
2
4
1
1
1 60

 5
1 12
1
1
41
13
17 528

 44
1
12
1
1
Entonces la ecuación de la circunferencia buscada es:
x2  y 2  Dx  Ey  F  0
I 
x2  y 2  7 x  5 y  44  0
Respuesta.
5.- Hallar la ecuación de la circunferencia circunscrita al triángulo de lados:
R1 : x  y  2  0 ; R2 : 2 x  3 y  1  0 ;
R3 : 4 x  y  17  0
Solución.
R1 : x  y  2  0 ; R2 : 2 x  3 y  1  0
Resolviendo R1 y R2 :
;
R3 : 4 x  y  17  0
Pág. 7 de 12
LIMBERT AYZACAYO CHOQUE
x  y  2  0   2 
2 x  2 y  4  0 


 Sumando ambas ecuaciones
2 x  3 y  1  0
2x  3 y 1  0 
5y  5  0

y 1
Reemplazando y  1 ; en R1
x y20

x 1  2  0  x  1
Entonces el punto de intersección es: C  1,1
Resolviendo
R1
y R3 :
x y20 
 Sumando las dos ecuaciones: 5x 15  0  x  3
4 x  y  17  0 
Reemplazando x  3 en R1 :
x y20
 3 y  2  0 
y 5
Entonces el punto de intersección es: A  3,5 
Resolviendo
R2
y R3 :
2 x  3 y  1  0   2 
4 x  6 y  2  0


 Sumando ambas ecuaciones
4 x  y  17  0
4 x  y  17  0 
5 y  15  0  y  3
Reemplazando y  3 en R3 :
4 x  y 17  0
 4 x  3 17  0
 x5
Entonces el punto de intersección es: B  5, 3
A, B, C en la ecuación general de la circunferencia:
x2  y 2  Dx  Ey  F  0
32  52  3D  5E  F  0
 3D  5E  F  34  I 
Reemplazando los puntos
52   3  5D  3E  F  0

5D  3E  F  34
 1

 D  E  F  2
2
2
 12  D  E  F  0
 II 
 III 
Resolviendo el sistema de ecuaciones:
3D  5E  F  34 

5D  3E  F  34 
 D  E  F  2 

8
34
F 
5
5
2
2
Reemplazando en la ecuación x  y  Dx  Ey  F  0
32
8
34
x2  y 2  x  y   0
5
5
5
D
32
5
E
Respuesta.
Pág. 8 de 12
LIMBERT AYZACAYO CHOQUE
6.- Dada la parábola
y 2  20 x , hallar la ecuación de la cuerda que pasa por el punto A  2,5 , de modo
que este punto divida a la cuerda en la mitad.
Solución.
P1  x1 , y1 
Reemplazando
P2  x2 , y2 
;
P1 , P2 en la ecuación de la parábola:
y12  20 x1
y2 2  20 x2
Restando las ecuaciones:
y12  y22  20 x1  20 x2
 y1  y2  y1  y2   20  x1  x2 

y1  y2
 y1  y2   20
x1  x2
I 
Por el punto medio se tiene:
5
y1  y2
2
Reemplazando

 II 
y1  y2
10  20
x1  x2
m  pendiente
 II 
y1  y2  10
en  I 

y1  y2
2
x1  x2

m2
Aplicando la ecuación punto pendiente de la recta:
y  y1  m  x  x1 

y  5  2  x  2

y  5  2x  4
R : 2x  y 1  0
Respuesta.
Pág. 9 de 12
LIMBERT AYZACAYO CHOQUE
7.- Un cable forma una parábola con torres de 220 m de altura, separadas en 1500 m. El punto
más bajo del cable está a 70 m de altura. Hallar la altura del cable a 150 m de la base de una torre.
Solución.
P1  750, 220
P2  0,70 
;
P3  750, 220 
;
Reemplazando los puntos en la ecuación general de la parábola:
 750
2
 750D  220E  F  0
0  0D  70E  F  0
2
 750
2
 750D  220E  F  0
Sumando ecuaciones
I 
y

 750D  220E  F  562500  0

70E  F  0

750D  220E  F  562500  0
 II 

 IV  :
  2 

Reemplazando

440 E  2 F  1125000  0
 IV 
y
70 E  F  0

440 E  2 F  1125000  0 
E  3750
Reemplazando E en la ecuación  II 
70E  F  0
I 
 II 
 III 
 III  :
750 D  220 E  F  562500  0

750 D  220 E  F  562500  0
Resolviendo ecuaciones
x2  Dx  Ey  F  0
140 E  2 F  0


440E  2F  1125000  0
70  3750  F  0


300 E  1125000  0
F  262500
E y F en la ecuación  I 
D0
La ecuación de la parábola es:
x2  Dx  Ey  F  0
x2  3750 y  262500  0
Reemplazando x  600 en la ecuación de la parábola:
Pág. 10 de 12
LIMBERT AYZACAYO CHOQUE
 600
2
 3750 y  262500  0
Entonces la altura del cable a

3750 y  622500

y
150 m de la base de una torre es de: H  166 m
622500
 166
3750
Respuesta.
8.- Hallar el dominio y condominio de la función:
y
e e
2
x
x
Solución.
Dy : x 
Para hallar el dominio se tiene:
e x  e x
2
x
2 y  e  e x Multiplicando m / m por e x
y
2 ye x  e x e x  e x e x
e 
x 2
2 ye x   e x   1
2

 2 y ex  1  0
b  b 2  4ac
2a
; b  2 y
En nuestro caso: a  1
Recordando
ei
x
ex 
xi 
  2 y  
 2 y 
2 1
2 y  4 y2  4
2
2
 4 11
; c 1

2 y  4 y2  4
2
 2 y  4 y2  4 

ln  e x   ln 


2



 2 y  4 y2  4 
  ln 2 y  4 y 2  4  ln 2
x  ln 


2



2 y  4 y2  4  0


4 y2  4  0
 y1  1

 y2  1

 y  2
2 y  4 y2  4  0

2  2   4  2   4  0
2
Falso
y0
2 y  4 y2  4  0

2 0  4 0  4  0
2
Falso
Pág. 11 de 12
LIMBERT AYZACAYO CHOQUE
y2
2 y  4 y2  4  0
Cy :

2  2  4  2  4  0
2
Verdadero
y 1
Respuesta
Pág. 12 de 12
LIMBERT AYZACAYO CHOQUE