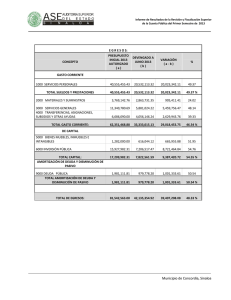
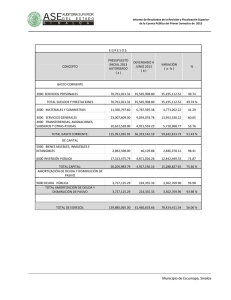
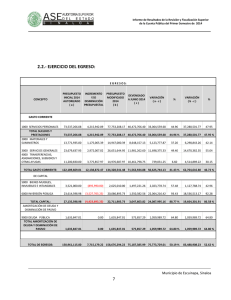
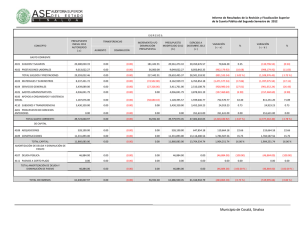
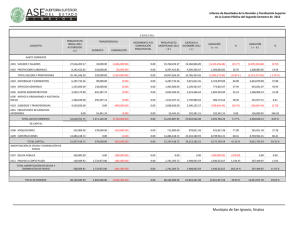
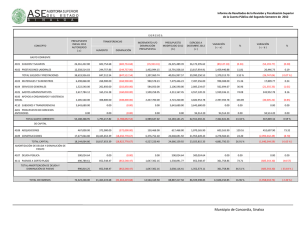
Amortización con interés simple:

Apuntes de Matemáticas Financieras
Prof. Gerardo Gutiérrez Jiménez
Amortización con interés simple:
Hay básicamente dos maneras de liquidar un crédito en efectivo, en bienes o servicios:
Con un desembolso único al final del plazo.
Con dos o más pagos, cuya frecuencia y tamaño pueden ser iguales o diferentes, y en este caso
se dice que el crédito se amortiza que significa dar muerte a la deuda (por sus raíces del latín, ad
y mortus).
Definición:
Amortizar es el proceso de cancelar una deuda y sus intereses mediante pagos periódicos.
Cuando el número de pagos es relativamente corto, el problema se resuelve considerando pagos
tras pagos como en los ejemplos que preceden; pero si son muchos, resulta poco práctico hacerlo
de esta manera y entonces se utilizan fórmulas que luego se justifican.
También es cierto que existen, por lo menos tres maneras diferentes de considerar los cargos
por intereses al amortizar un crédito:
a) Con interés global.
b) Con interés simple.
c) Con interés compuesto.
Amortización de renta fija.
En la amortización con interés global, los pagos son todos iguales, ya que el interés total se divide
entre el número de pagos y el resultado se suma al pago o capital, llamado amortización.
Es importante y oportuno señalar que abono y amortización son diferentes, ya que una parte de
cada abono es para cubrir los intereses del periodo, y la otra, es decir, la amortización, se destina
al capital que se adeuda haciendo que con cada pago se reduzca: esto es:
ABONO = Interés + AMORTIZACIÓN
Ejemplo: Amortización de un crédito con pagos fijos.
Fórmulas:
Intereses I = Ci
Amortización = Deuda/# pagos A = M/#;
Cada pago o abono R = I + A R = M/#
C = Capital o crédito.
¿Cuál es el abono mensual con el que se amortiza un préstamo de $90,000 en un año y
medio si se cargan intereses del 1.5% simple, es decir, global mensual? (Villalobos, 2007,
págs. 128-129)
Los intereses a pagar en cada mes están por I = C (i) donde:
C = 90,000, el valor de la deuda.
37
Apuntes de Matemáticas Financieras
Prof. Gerardo Gutiérrez Jiménez
i = 0.015 la tasa de interés mensual.
t = 18 meses.
R = ¿?
I = Ci ; I = 90,000 (0.015); I = $1,350
M = C (1 + it)
M = 90,000 (1 + 0.015(18)
M = $ 114,300,
El tiempo “t” no se divide entre 12 ya que la tasa de interés está dada mensualmente, es decir
queremos el pago mensual.
A=C/#
A = 90,000 / 18
A= 5,000
El abono no tiene intereses, por lo que se tomó el capital y no el monto.
R=I+A
R = 1,350 + 5,000
R = 6,350
R = M/#
R = 114,300 / 18
R = $6,350
Ejemplo:
¿De qué tamaño es el crédito que se amortiza con 13 pagos semanales de $2,500 con
intereses globales del 7.54%? (Villalobos, 2007, págs. 129-130)
Ejemplo:
Los intereses en cada pago se calculan sobre un saldo insoluto.
Amortización de un crédito con renta variable:
Usted compra un televisor de $6,500 con un pago inicial del 20%, y después 8 abonos
mensuales con pagos del 12% simple anual sobre saldos insolutos (aquello que no ha sido
pagado). Hallar los pagos y los intereses. (Villalobos, 2007, págs. 130-131)
Datos:
Compra del TV = $6,500
Pago inicial: 20%
Amortización Abono = 8 mensualidades
Cargos = 12% sobre saldos insolutos.
I = ¿?
R = ¿?
38