Mostreig i quantificació

PRÀCTICA 1
MOSTREIG I QUANTIFICACIÓ
MOSTREIG
DEFINICIÓ
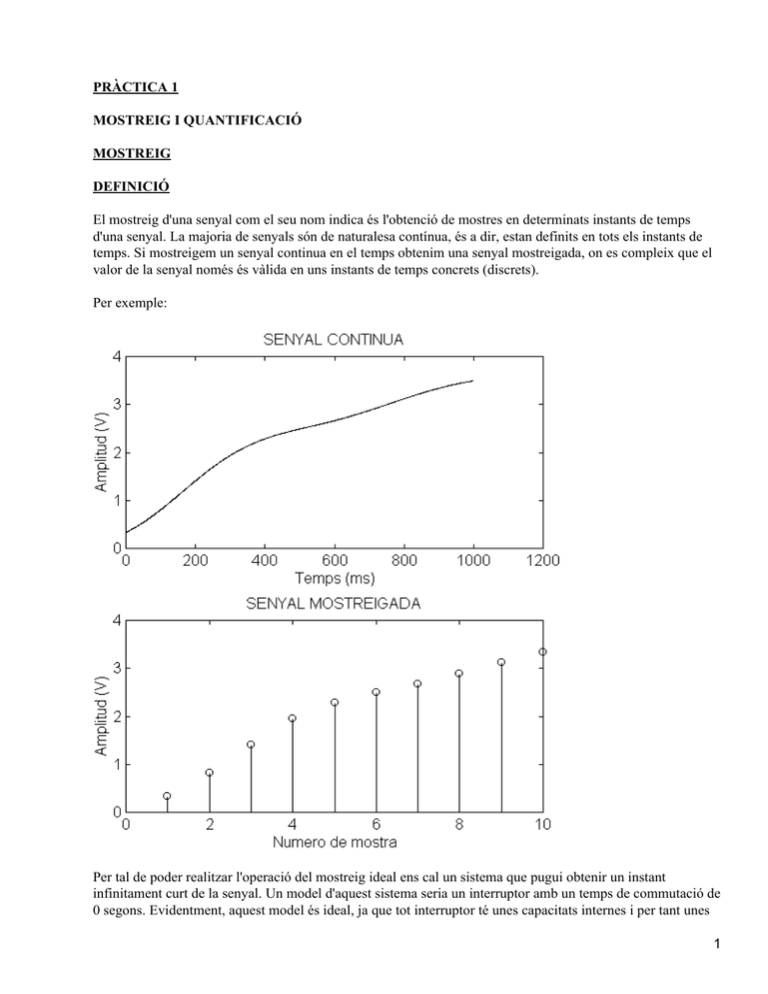
El mostreig d'una senyal com el seu nom indica és l'obtenció de mostres en determinats instants de temps
d'una senyal. La majoria de senyals són de naturalesa contínua, és a dir, estan definits en tots els instants de
temps. Si mostreigem un senyal continua en el temps obtenim una senyal mostreigada, on es compleix que el
valor de la senyal només és vàlida en uns instants de temps concrets (discrets).
Per exemple:
Per tal de poder realitzar l'operació del mostreig ideal ens cal un sistema que pugui obtenir un instant
infinitament curt de la senyal. Un model d'aquest sistema seria un interruptor amb un temps de commutació de
0 segons. Evidentment, aquest model és ideal, ja que tot interruptor té unes capacitats internes i per tant unes
1
constants de temps diferents de zero que provoquen que el temps en que tenim la mostra no sigui diferencial i
tingui una durada determinada. Per tant, un model de mostreigador més real és un tren de polsos p(t) amb una
amplitud de 1 durant un interval molt petit.
El concepte de mostreig es pot entendre com una multiplicació temporal del senyal original amb un tren de
deltes (cas ideal) o de polsos p(t) (cas real).
Un cop mostreigada una senyal tenim que el seu espectre és el de la senyal sense mostreigar però es va
repetint cada Fs (Sample frequency). Per tal de poder recuperar la senyal cal que es compleixi el critèri de
Nyquist de tal forma que no hi hagi aliasing. En la recuperació s'utilitza un filtre passa−baixes per tal de
quedar−nos tant sols amb la informació compresa a la banda que ens interessa, és a dir, de 0Hz a Fs/2. Aquest
filtre es pot entendre des del punt de vista temporal com una convolució de la senyal mostreigada amb una
sinc. Si fem aquest procés d'una manera gràfica obtenim:
Podem veure que la suma de les contribucions de totes les sinc fan que obtinguem la senyal recuperada
idèntica a la original.
Si considerem que el mostreigador no és ideal tenim que no podem recuperar mai la senyal original d'una
manera exacta, ja que la transformada de Fourier d'un pols és una funció sinc, i la multiplicació d'una funció
sinc amb l'espectre de la senyal original dóna l'espectre de la senyal original lleugerament modificat i repetit
cada Fs. A continuació podem veure com es modifica l'espectre original de la senyal al fer un mostreig amb
un pols de durada Tp=Ts. Com es pot observar, tenim un espectre molt semblant al original en les baixes
freqüències, però a mesura que ens acostem a Fs/2 tenim que la diferència entre l'espectre original i el
resultant són més diferents.
2
EL TEOREMA DE NYQUIST
El teorema de Nyquist diu que cal mostreigar una senyal com a mínim a una freqüència de mostreig de dues
vegades la freqüència màxima de la senyal per tal de poder−la reconstruir posteriorment sense cap mena
d'alteració.
Això és degut a que al fer el mostreig d'una senyal tenim que l'espectre de la senyal mostreigada queda repetit
amb un periode igual a la freqüència de mostreig.
Això es pot il.lustrar amb un exemple a on suposem una senyal que té un espectre triangular (forma espectral
genèrica i aproximada de molts dels senyals):
Al tenir aquest espectre, tenim que per tal que no hi hagi solapament de l'espectre desitjat i la seva rèplica
degut a l'efecte del mostreig cal que:
FS>2*fMAX
En el cas de no complir la condició de Nyquist tenim que l'espectre del senyal desitjat amb l'espectre repetit
degut al mostreig se solapen (fenomen anomenat `aliasing'). En el cas de tenir aliasing, la recuperació del
senyal original sense cap alteració és impossible.
Cal dir que la condició de Nyquist és el cas límit i suposant que podem implementar filtres d'ordre infinit.
Com que això no és possible cal aplicar un criteri una mica més restrictiu com per exemple que Fs>4*fMAX,
ja que així deixem un marge més gran entre l'espectre desitjat i la rèplica per tal de poder filtrar amb un filtre
passa−baixes realitzable.
CAS PRÀCTIC
A continuació vaig a il.lustrar aquests conceptes amb un cas pràctic. En aquest cas s'ha agafat una senyal de
3
veu mostreigada a 8KHz, quantificada a 8 bits amb PCM i amb un únic canal (mono). La frase que es diu en
la senyal és: Habia sido un día de los que parecen un test de resistencia
Seguidament tenim el senyal original i el seu espectre corresponent:
De la gràfica de l'espectre podem observar que la senyal que ens interessa és la que va de 0Hz fins a 4KHz, ja
que la resta és la repetició de l'espectre (freqüències negatives). Al realitzar el mostreig a 8KHz i tenint en
compte que la veu humana pot arribar a 15KHz tenim que no estem complint el criteri de Nyquist i per tant
aquesta senyal té `aliasing'. L'espectre real de la senyal, mostreigada a 44KHz mostra que el senyal original té
components per sobre dels 4 KHz i per tant que no estem complint el criteri de Nyquist.
4
Com es pot observar en l'espectre de la senyal original mostreigada a 44KHz tenim que la major part de
potència de la senyal està compresa en la banda de 0Hz−4KHz, però cal dir que la senyal té components
frequencials de fins a 20KHz. Per tant la senyal de partida té `aliasing'.
Per tal de simplificar la pràctica suposaré que la senyal original és la senyal de veu mostreigada a 4KHz amb
`aliasing' inclòs i que la banda de la senyal original és de 4KHz.
A partir d'aquí es fa una interpolació per tal d'augmentar la freqüència de mostreig fins a 22KHz. Per fer−ho
només cal agafar la senyal original i per cada mostra intercal.lar dues mostres a zero. En la següent gràfica es
mostra la interpolació.
5
Al realitzar l'operació d'interpolació hem elevat la freqüència de mostreig a 22KHz i per tant ens apareix
l'espectre de la senyal original repetit tres cops:
6
A continuació realitzem un filtrat d'aquesta senyal interpolada de tal forma que només ens quedem amb la part
de l'espectre que correspondria a la senyal original de 4KHz d'amplada de banda mostreigada a 22KHz. Això
ho fem mitjançant un filtre ideal que consisteix en agafar l'espectre de la senyal interpolada i posar a zero les
freqüències que estan entre 4KHz i 18KHz. Aquest filtrat no és realitzable a la vida real, ja que per tal de
realitzar el filtrat ens cal conèixer totes les mostres de la senyal i requereix una potència de càlcul increïble.
Si filtrem la senyal obtenim:
7
A partir d'aquest punt és com tenir una senyal de veu de una banda de 0−4KHz i mostreigada a 22KHz.
A continuació per mostrar l'aliasing només cal fer un delmat per 4 de tal forma que la freqüència equivalent
de mostreig serà de 6KHz i per tant tindrem aliasing en la banda de 2KHz−3KHz.
8
Com es pot observar, la banda de 2KHz−3KHz ha quedat modificada degut a l'aliasing que hem introduït.
Com es pot observar, l'efecte de l'aliasing provoca que tinguem un solapament de l'espectre de la senyal
original invertit i a la part alta de la banda de freqüències.
PROGRAMA UTILITZAT:
Per tal de poder realitzar totes les gràfiques anteriors he utilitzat les següents funcions:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%
% Interpolació %
% PARÀMETRES: %
% x => Senyal a interpolar %
% Rfi=> Relació freq. final / freq. inicial %
9
% RETORNA: %
% y => Senyal interpolada %
%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function y = interpol(x,Rfi)
y = zeros(1,Rfi*length(x));
y(1:Rfi:length(y)) = x;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%
% Delmat %
% PARÀMETRES: %
% x => Senyal a fer delmat %
% Rfi => Relació freq. Final/freq. Inicial %
% RETORNA: %
% y => Senyal delmada %
%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function y = delmat(x,Rfi)
y = x(1:Rfi:length(x));
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%
% Filtre passa−baixes ideal %
% PARÀMETRES: %
% x => Senyal a filtrar %
% fs => freqüència a filtrar %
% RETORNA: %
10
% y => Senyal filtrada %
%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function y = LPFIdeal(x,fs,b)
Dummy = find(x>fs); % Busquem valors que passen el fs
Dummy(fc+1:length(Dummy)−fc)=zeros(length(Dummy)−2*fc,1); % Eliminem banda alta
y = ifft(Dummy,length(x)); % Realitzem la transformada inversa
y = real(y); % Part real per si errors de decimals
El programa general utilitzat per a generar les gràfiques és:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%
% Demostració de la teoria del mostreig %
%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
i=1;
if Figura == 0 Figura=1;
end;
while i ~= Figura
close(figure(i));
i=i+1;
end;
clear all;
Tecla=0;
Figura=1;
while Tecla ~=6
Tecla=MENU('Mostreig i Quantificació','Carregar variable','Interpolar','Filtrar','Delmat','Sortir');
11
if Tecla == 1
[So,Fs]=wavread('test.wav'); %Llegim arxiu de veu original
Temp=size(So); %Convertim si cal vector de veu a taula de n elements
if Temp(1) == 1 then
So=So';
end
So=So−mean(So); %Elimina la mitja del so
figure(Figura);
subplot(2,1,1);
plot(So); %Mostra el senyal de veu original
TITLE('SENYAL ORIGINAL');
XLABEL('Nº mostres');
subplot(2,1,2);
SoTmp=20*log10(abs(fft(So)));
w=Fs/length(SoTmp):Fs/length(SoTmp):Fs; %Mostra eix de freqüència
plot(w,SoTmp); %Mostra la fft del senyal original
axis([1,Fs,0,max(SoTmp)]) %modifiquem escala
TITLE('DENSITAT ESPECTRAL DE POTÈNCIA DEL SENYAL ORIGINAL');
XLABEL('Freqüència (Hz)');
YLABEL('Potència (dB)');
clear SoTmp;
Figura=Figura+1;
elseif Tecla == 2
Rfi=input('Relació ff/fi: ');
SoInterpol=Interpol(So,Rfi);
%Mostrem com s'han afagit mostres a la senyal original
12
figure(Figura);
subplot(2,1,1);
stem(So(1:60/Rfi)); %Mostrem interpolació
TITLE('MOSTRES DEL SENYAL ORIGINAL');
XLABEL('Nº mostres');
subplot(2,1,2);
stem(SoInterpol(1:60));
TITLE('MOSTRES DEL SENYAL INTERPOLAT');
XLABEL('Nº mostres');
Figura=Figura+1;
%Mostrem els espectres dels senyals original i interpolat
figure(Figura);
EspectreTmp=fft(So);
Espectre1=20*log10(abs(EspectreTmp));
subplot(2,1,1);
w=Fs/length(Espectre1):Fs/length(Espectre1):Fs;
plot(w,Espectre1);
axis([1,Fs*Rfi,0,max(Espectre1)]) %modifiquem escala
TITLE('ESPECTRE DE LA SENYAL ORIGINAL');
XLABEL('Freqüència(Hz)');
YLABEL('Potència (dB)');
EspectreTmp=fft(SoInterpol);
Espectre2=20*log10(abs(EspectreTmp));
subplot(2,1,2);
w=Fs*Rfi/length(Espectre2):Fs*Rfi/length(Espectre2):Fs*Rfi;
plot(w,Espectre2);
13
axis([1,Fs*Rfi,0,max(Espectre2)]) %modifiquem escala
TITLE('ESPECTRE DE LA SENYAL INTERPOLADA');
XLABEL('Freqüència (Hz)');
YLABEL('Potència (dB)');
Figura=Figura+1;
elseif Tecla ==3
Fc = input('Frequencia de tall: ');
Fc=Fc* (length(SoInterpol)/(Rfi*Fs)); %Convertim fc a num mostres
SoFiltrat=LPFIdeal(SoInterpol,Fc);
%Mostrem espectre de senyal interpolada abans i després de filtre
figure(Figura);
subplot(2,1,1);
SoTmp=20*log10(abs(fft(SoInterpol)));
w=Fs*Rfi/length(SoTmp):Fs*Rfi/length(SoTmp):Fs*Rfi;
plot(w,SoTmp);
axis([1,Fs*Rfi,0,max(SoTmp)]) %modifiquem escala
TITLE('ESPECTRE DE LA SENYAL INTERPOLADA');
YLABEL('Potència (dB)');
XLABEL('Freqüència (Hz)');
clear SoTmp;
subplot(2,1,2);
SoTmp=20*log10(abs(fft(SoFiltrat)));
w=Fs*Rfi/length(SoTmp):Fs*Rfi/length(SoTmp):Fs*Rfi;
plot(w,SoTmp);
axis([1,Fs*Rfi,0,max(SoTmp)]) %modifiquem escala
TITLE('ESPECTRE DE LA SENYAL FILTRADA');
14
YLABEL('Potència (dB)');
XLABEL('Freqüència (Hz)');
Figura=Figura+1;
FInterpol=Fs*Rfi;
elseif Tecla==4
Rfi=input('Relació ff/fi: ');
SoDelmat=Rfi*delmat(SoFiltrat,Rfi);
%Mostrem la delmació
figure(Figura);
subplot(2,1,1);
stem(So(1:60));
subplot(2,1,2);
stem(SoDelmat(1:60/Rfi));
Figura=Figura+1;
%Mostrem els espectres de la senyal original i de la delmada
figure(Figura);
subplot(2,1,1);
Espectre1=20*log10(abs(fft(So)));
w=Fs/length(Espectre1):Fs/length(Espectre1):Fs;
plot(w,Espectre1,'g'); %Mostrem en verd l'espectre de la original
axis([1,Fs,0,max(Espectre1)])
TITLE('ESPECTRE DE LA SENYAL ORIGINAL');
YLABEL('Potència (dB)');
XLABEL('Freqüència (Hz)');
subplot(2,1,2);
Espectre2=20*log10(abs(fft(SoDelmat)));
15
w=FInterpol/(length(Espectre2)*Rfi):FInterpol/(length(Espectre2)*Rfi):FInterpol/Rfi;
plot(w,Espectre2,'r'); %Mostrem en vermell l'espectre de la tractada
axis([1,FInterpol/Rfi,0,max(Espectre2)])
TITLE('ESPECTRE DE LA SENYAL DELMADA');
YLABEL('Potència (dB)');
XLABEL('Freqüència (Hz)');
Figura=Figura+1;
end;
end;
QUANTIFICACIÓ
La quantificació no és altre cosa que un procés de discretització de les possibles amplituds d'un senyal. Partim
d'un senyal d'amplitud contínua i al realitzar la quantificació permetem que la senyal pugi valer tant sols un
numero finit de possibles valors. A aquest procés se l'anomena quantificació. Quan els intervals dels possibles
valors estan situats de manera equiespaiada, llavors tenim una quantificació linial.
Un exemple de la quantificació linial es pot veure en el següent gràfic, a on tenim una senyal d'entrada
contínua i una senyal que és fruit de la quantificació linial amb 16 nivells de la primera i la seva posterior
desquantificació:
16
Alhora de quantificar una senyal per al seu tractament digital posterior hem de realitzar un doble procés. En
primer lloc cal assignar uns intervals de quantificació en els quals tenim que qualsevol valor que estigui
comprès dins l'interval es quantificarà amb el valor de l'interval. Per altre banda, cal tenir en compte que per
tal de poder tractar adequadament la senyal de forma digital cal codificar tots els intervals d'una forma que
sigui senzilla per al processador i per tant cada interval ha d'estar codificat amb un numero enter i el numero
d'intervals ha de ésser una potència de dos per tal d'optimitzar el numero de bits utilitzats en la codificació de
cada interval.
Així doncs, un quantificador linial és un quantificador que té els nivells de quantificació equiespaiats i per tant
queda determinat amb els següents paràmetres:
Nivells de quantificació: És el numero de possibles valors que podem assignar a la senyal quantificada.
Aquest valor pot venir donat directament o amb numero de bits dels que disposem per tal de quantificar la
senyal. Aleshores tindrem 2^bits nivells de quantificació.
Fons d'escala: És el valor màxim de la senyal original que podem arribar a quantificar sense tenir saturació.
Pas per zero: Podem indicar si un dels nostres intervals val zero (quantificador amb pas per zero) o si per
contra, tenim un quantificador que no té cap interval de valor zero (sense pas per zero).
Interval de quantificació (): És l'amplitud del senyal que inclou un interval de quantificació. En el cas del
quantificador linial, l'interval de quantificació és constant per tots els possibles valors de quantificació.
Per tal de recuperar la senyal cal fer un simple canvi d'escala. Aquest canvi és degut a que tenim la senyal
discretitzada i codificada en nivells. Aquests nivells cal fer que corresponguin a l'escala de la senyal original i
per tant multiplicant el valor del nivell per l'interval de quantificació tenim una senyal d'amplitud igual a la de
la senyal d'entrada.
SOROLL DE QUANTIFICACIÓ:
Cal tenir en compte que si quantifiquem una senyal i la desquantifiquem mai tindrem la mateixa senyal que la
original, ja que durant el procés de quantificació tenim certa pèrdua d'informació. La pèrdua d'informació
deguda al simple fet de la quantificació és el què s'anomena com a soroll o error de quantificació. Aquest
error és degut a que al realitzar l'assignació de tots els valors de un interval a un únic valor cometem un error
d'arrodoniment i això provoca que la senyal original i la senyal quantificada siguin diferents i per tant que hi
hagi un soroll de quantificació. Aquest error com a màxim serà d'una amplitud de /2, ja que és l'error màxim
que podem cometre.
Si fem la funció distribució de probabilitat de l'error tenim que es tracta d'un soroll pla entre −/2 i com el de
la figura.
Com que podem aproximar la funció densitat de probabilitat com plana podem dir que la potència de soroll
degut a la quantificació és:
Si fem el càlcul de la potència de soroll tenim que la potència de soroll val:
17
Quan el quantificador no treballa adequadament, és a dir, quan el fons d'escala no està ajustat adequadament a
la senyal a quantificar ens apareixen dos tipus de soroll nous que si que estan correlats amb la senyal i per tant
no es poden considerar com a soroll blanc. Aquests tipus de soroll són els següents:
Soroll de overflow: Aquest soroll és degut a tenir un fons d'escala per sota del valor màxim de la senyal. Això
provoca que el nostre quantificador saturi (retalli) la senyal d'entrada i per tant el soroll que es defineix com la
diferència entre la senyal d'entrada i la recuperada pren valors elevats i la forma del senyal d'error està
totalment correlada amb el senyal a quantificar.
Soroll de underflow: Aquest soroll és degut a tenir un fons d'escala massa gran respecte el màxim de la
senyal. Això provoca que, en el cas del quantificador amb pas per zero, la senyal recuperada valgui zero,
mentre que en el quantificador sense pas per zero obtenim una sortida que oscil.la degut a petites fluctuacions
(soroll) de l'entrada.
A continuació tenim un exemple de una senyal quantificada en la que es poden observar els tres tipus de
soroll, en el cas del quantificador amb pas per zero i en el cas del quantificador sense pas per zero. En el
primer segment de la gràfica es pot observar el soroll per underflow, al segment central del gràfic es pot
observar el soroll degut exclusivament a la quantificació amb un fons d'escala adequat, i en l'últim tros de la
gràfica (quan la senyal supera el fons d'escala) podem observar el soroll per overflow.
Senyal original
Senyal quantificat i recuperat
Error de quantificació
18
19
SNR EN FUNCIÓ DEL FONS D'ESCALA:
A continuació tenim la gràfica de la SNR en funció del fons d'escala per diferents numeros de bits i pel
quantificador amb pas per zero i sense pas per zero. Com es pot observar en les diferents gràfiques tenim que
l'eix de coordenades està expressat en funció de FS/4(x) això és degut a que normalment s'utilitza la cota de
4(x) per al fons d'escala ja que la veu humana té unes característiques que demostren que utilitzant aquest
valor per al fons d'escala obtenim la millor relació entre soroll de quantificació i soroll per overflow.
En les gràfiques de acontinuació podem veure tres zones diferents.
Saturació: és la zona de l'esquerra, ja que tenim un fons d'escala molt petit. En aquesta zona podem observar
que la SNR és molt baixa, però que puja ràpidament a mesura que augmentem el fons d'escala
Zona central: en aquesta zona tenim que el fons d'escala està ajustat a l'amplitud de la senyal. En el punt on la
SNR és màxima tenim que el fons d'escala coincideix amb el màxim de la senyal dividit per 4 vegades la
20
desviació típica, i a mesura que anem augmentant el fons d'escala anem augmentant el soroll de quantificació i
per tant la SNR baixa.
Underflow: és la zona de la dreta, ja que tenim un fons d'escala massa gran. En aquesta zona tenim que la
SNR és molt baixa, degut a que tenim un senyal que té poca excursió respecte el fons d'escala que tenim i per
tant l'error de quantificació és molt elevat.
21
La única diferència entre el quantificador amb pas per zero i el quantificador sense pas per zero és que en el
cas del quantificador amb pas per zero tenim un punt que el fons d'escala és tant gran que la senyal
desquantificada sempre val zero i per tant el soroll, que és la diferència entre la senyal original i la
desquantificada, val igual que el senyal i per tant la SNR tendeix a ésser 1 (0dB). En canvi, en el cas del
quantificador sense pas per zero, tenim que el fons d'escala és va fent més gran i per tant tenim que la senyal
desquantificada va oscil.lant en torn el zero per canvis de signe de la senyal i per tant la potència de soroll és
la d'una senyal quadrada que oscil.la entre +/2 i −/2, però al augmentar el FS tenim que va augmentant i
per tant la potència de soroll també va augmentant i per tant tenim que la SNR va disminuint.
PROGRAMA UTILITZAT:
So=wavread('test.wav'); %Carreguem variable de veu
So=So−mean(So); %Treiem component de continua
if max(So)>abs(min(So)) %Calculem el màxim de la senyal
Max=max(So);
else
Max=abs(min(So));
end;
S=10*log10(So'*So); %Calculem potència de senyal
for Bits=2:5, %Fem gràfiques per de 2 a 5 bits
22
i=1;
for Escala=0.5:0.5:4*Max,
SoQ=QuanLin(So,Escala,Bits,1); %Quantifiquem la senyal
SoDeQ=DeQuan(SoQ,Escala,Bits,1); %Desquantifiquem la senyal
Error=So−SoDeQ; %Calculem error
N=10*log10(Error'*Error); %Calculem la potència de soroll
SNR(i)=S−N; %Calculem la SNR
FS(i)=Escala/(4*std(So));
i=i+1;
end
plot(FS,SNR); %Mostrem la gràfica resultant
hold on
end
hold off
xlabel('FS/4*std');
ylabel('SNR (dB)');
TITLE('SNR vs FS PER AL QUANTIFICADOR SENSE PAS PER ZERO');
SNR EN FUNCIÓ DEL NUMERO DE BITS
La gràfica que s'ha obtingut de la SNR en funció dels bits del quantificador és la següent:
23
En la segona gràfica tenim la diferència en dB entre la SNR per n+1 bits i la SNR per n bits. Com es pot
observar, ens mantenim molt aprop del resultat teòric de que cada bit representa una millora de 6dB en la
SNR. Aquest límit teòric s'obté de considerar que la funció densitat de probabilitat de l'error de quantificació
és plana entre +/2 i −/2. Desenvolupant tots els càlculs s'obté que la SNR en funció del numero de bits
segueix la forma de:
PROGRAMA UTILITZAT:
So=wavread('test.wav'); %Carrega variable de veu
So=So−mean(So); %Treu la mitja del senyal
if max(So)>abs(min(So)) %Obtenim el valor màxim de la senyal
Max=max(So);
else
Max=abs(min(So));
24
end;
S=10*log10(So'*So); %Calculem la potència de senyal
for Bits=1:16, %Fem gràfica de 1 a 16 bits
SoQ=QuanLin(So,Max,Bits,0); %Quantifiquem la senyal amb el numero de bits adequat
SoDeQ=DeQuan(SoQ,Max,Bits,0); %Desquantifiquem la senyal de veu
Error=So−SoDeQ; %Calculem l'error associat a la quantificació
N=10*log10(Error'*Error); %Calculem la potència de soroll
SNR(Bits)=S−N; %Calculem la SNR
end
subplot(2,1,1); %Mostrem la gràfica de SNR vs Bits
plot(SNR);
xlabel('Numero de bits');
ylabel('SNR (dB)');
TITLE('SNR vs Numero de bits');
subplot(2,1,2);
for i=1:15, %Mostrem les diferències entre bits consecutius
Dif(i)=SNR(i+1)−SNR(i);
end
plot(Dif);
xlabel('Numero de bits');
ylabel('SNR(i+1)−SNR(i) ');
ESPECTRE DEL SOROLL DE QUANTIFICACIÓ
Anem a veure l'espectre del soroll de quantificació. Per fer−ho només cal obtenir l'error de quantifiació i
fer−ne la transformada de fourier.
25
Com es pot observar, a mesura que augmentem el numero de bits tenim que l'error de quantificació es fa més
incorrelat amb el senyal i per tant tenim que el seu espectre és més pla i per tant es pot aproximar a soroll
gaussià blanc.
PROGRAMA UTILITZAT:
So=wavread('test.wav'); %Carrega variable de veu
So=So−mean(So); %Treu la mitja del senyal
if max(So)>abs(min(So)) %Obtenim el valor màxim de la senyal
Max=max(So);
else
Max=abs(min(So));
end;
f=8000/length(So):8000/length(So):8000; %Calculem eix per canvi escala de les x
i=1;
26
for Bits=2:4:10, %Fem analisi per 2, 6 i 10 bits
SoQ=QuanLin(So,Max,Bits,0); %Quantifiquem
SoDeQ=DeQuan(SoQ,Max,Bits,0); %Desquantifiquem
Error=So−SoDeQ; %Calculem error
EError=abs(10*log10(fft(Error))); %Fem espectre de l'error
subplot(3,1,i); %Representem l'espectre
i=i+1;
plot(f,EError);
ylabel('Potència (dB)');
end
xlabel('Freqüència (Hz)');
Processat del senyal
1
19
f
Espectre de potència de la senyal original
fMAX
fMAX
f
Espectre de potència de la senyal mostreigada
FS
/2
−/2
1/
f(n)
27