Tema 5. Normalización Introducción Anomalías de actualización

Introducción
Tema 5. Normalización
•
Dependencias funcionales y normalización en BD
relacionales Elmasri/Navathe 02
Hasta ahora hemos hecho
empleando el sentido común.
•
Algoritmos de diseño de BD relacionales y dependencias
adicionales Elmasri/Navathe 02
Los atributos se han agrupado en relaciones de una
forma natural y lógica.
•
Hay agrupaciones que pueden ser mejores que
otras: hace falta una “medida formal” de la bondad
de los diseños.
•
A continuación veremos que, en general, se tiende a
disminuir:
Methodology – Monitoring and tunning of the operational
system Connolly/Begg02
• Introducción (14.1)
diseños
• Dependencias funcionales (14.2)
– Anomalías de actualización
redundancia en tuplas
• Descomposición de relaciones (15.1)
– Valores nulos
• Formas normales (14.3, 14.4, 14.5)
– Tuplas espurias
de
BD
debidas
a
• Desnormalización
© A. Jaime, C. Domínguez 2005
DBD Tema 5
1
© A. Jaime, C. Domínguez 2005
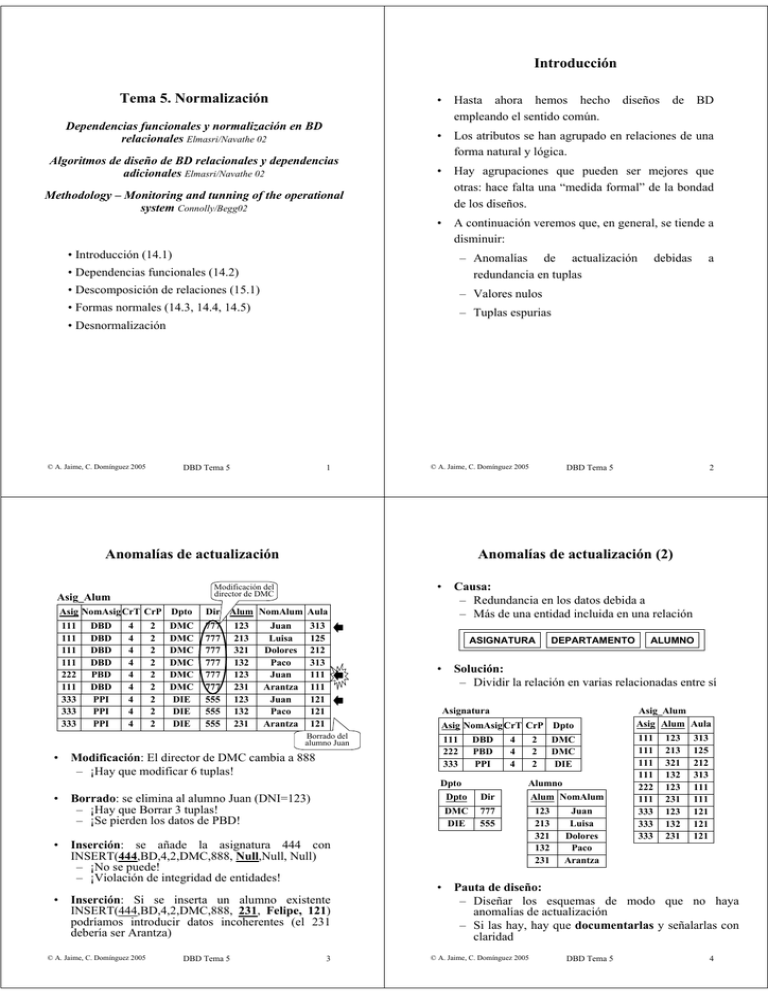
Anomalías de actualización
•
Asig NomAsig CrT CrP Dpto
Dir Alum NomAlum Aula
111
111
111
111
222
111
333
333
333
777
777
777
777
777
777
555
555
555
DBD
DBD
DBD
DBD
PBD
DBD
PPI
PPI
PPI
4
4
4
4
4
4
4
4
4
2
2
2
2
2
2
2
2
2
DMC
DMC
DMC
DMC
DMC
DMC
DIE
DIE
DIE
123
213
321
132
123
231
123
132
231
Juan
Luisa
Dolores
Paco
Juan
Arantza
Juan
Paco
Arantza
313
125
212
313
111
111
121
121
121
•
•
•
Inserción: se añade la asignatura 444 con
INSERT(444,BD,4,2,DMC,888, Null,Null, Null)
– ¡No se puede!
– ¡Violación de integridad de entidades!
•
Inserción: Si se inserta un alumno existente
INSERT(444,BD,4,2,DMC,888, 231, Felipe, 121)
podríamos introducir datos incoherentes (el 231
debería ser Arantza)
111
222
333
3
DBD
PBD
PPI
Dpto
Dpto
Dir
DMC
DIE
777
555
•
ALUMNO
Solución:
– Dividir la relación en varias relacionadas entre sí
Asignatura
Borrado: se elimina al alumno Juan (DNI=123)
– ¡Hay que Borrar 3 tuplas!
– ¡Se pierden los datos de PBD!
DBD Tema 5
DEPARTAMENTO
Asig NomAsig CrT CrP Dpto
Modificación: El director de DMC cambia a 888
– ¡Hay que modificar 6 tuplas!
© A. Jaime, C. Domínguez 2005
Causa:
– Redundancia en los datos debida a
– Más de una entidad incluida en una relación
ASIGNATURA
Borrado del
alumno Juan
•
2
Anomalías de actualización (2)
Modificación del
director de DMC
Asig_Alum
DBD Tema 5
4
4
4
2
2
2
DMC
DMC
DIE
Alumno
Alum NomAlum
123
213
321
132
231
Juan
Luisa
Dolores
Paco
Arantza
Asig_Alum
Asig Alum Aula
111
111
111
111
222
111
333
333
333
123
213
321
132
123
231
123
132
231
313
125
212
313
111
111
121
121
121
Pauta de diseño:
– Diseñar los esquemas de modo que no haya
anomalías de actualización
– Si las hay, hay que documentarlas y señalarlas con
claridad
© A. Jaime, C. Domínguez 2005
DBD Tema 5
4
Valores NULL
•
•
•
•
Tuplas espurias
Almacenar valores NULL supone ocupar espacio
de manera innecesaria
Además pueden confundirse sus significados:
– No aplicable (N/A)
– Desconocido (Unknown)
– Pendiente (Pending)
Los nulos dificultan construcción de ciertas
consultas (ejemplo sumas y resto de funciones
agregadas)
Solución
– Si hay muchos NULL (permanentes), definir
más relaciones
•
•
NomAsig NomAlum Aula
PBD
DBD
DBD
PBD
Asig NomAsig
Asig NomAsig AulaVirtual
111
222
444
555
777
888
111
222
444
555
777
888
DBD
PBD
ABD
BD
MP
TP
1
null
null
2
null
null
PBD
DBD
DBD
PBD
© A. Jaime, C. Domínguez 2005
DBD
DBD
PBD
•
1
2
DBD Tema 5
5
318
121
330
NomAsig NomAlum Aula
PBD
DBD
DBD
DBD
DBD
PBD
Juan
Juan
Juan
Leire
Leire
Leire
Reunión (|X|)
330
318
121
318
121
330
Tuplas
espurias
Pauta de diseño:
– Las condiciones de una reunión deberían basarse
(por ejemplo) en la igualdad entre una clave
primaria y una extranjera que haga referencia a
dicha clave primaria: así no aparecen tuplas
espurias
© A. Jaime, C. Domínguez 2005
División de un esquema de relación
DBD Tema 5
6
Dependencia funcional (DF)
•
¿Cómo?
– Basándose en la semántica de los atributos:
Dependencia funcional
– Asegurando que no aparecen tuplas espurias al
reconstruir la relación original (sin pérdida de
información)
•
Necesitamos nomenclatura para nombrar a:
– Atributos relacionados con uno dado
– Relaciones entre atributos de un esquema de
relación
•
Juan
Juan
Leire
Leire
NomAsig Aula
DBD
PBD
ABD
BD
MP
TP
Tabla
original
330
318
121
330
NomAsig NomAlum
AsigVirtural
Asig AulaVirtual
111
555
Juan
Juan
Leire
Leire
Proyecciones (π)
Asignatura
Asignatura
Son las tuplas “inesperadas” del resultado de una
reunión.
Cuando aparecen “se pierde información”
... y relacionarla con otros conceptos de BD:
– Superclave
– Clave candidata
– Atributo primo
– ...
•
•
Se expresa como XÆY
Significa que conocido un valor de X, se identifica un
único valor de Y
– Siempre de acuerdo con el significado que se les
atribuyan a los atributos
– Será cierto para todos los posibles estados de la
BD (no solo para un estado concreto)
•
Por ejemplo:
– ¿NombreÆApellido?
– ¿DNIÆNombre? o lo que es lo mismo¿puede
haber dos nombres con el mismo DNI?
•
•
Sea R={A1, A2, ... , An} un esquema de relación
Sean X e Y subconjuntos de atributos de R (o sea
X⊆R e Y ⊆R)
Entonces se dirá que XÆY (Y depende funcionalmente de X) si:
– Para cualquier extensión r de R se verifica que
para todo par de tuplas t1, t2 de r:
•
t1.X = t2.X Æ t1.Y = t2.Y
© A. Jaime, C. Domínguez 2005
DBD Tema 5
7
© A. Jaime, C. Domínguez 2005
DBD Tema 5
8
Reglas de inferencia: Axiomas
Dependencia funcional (DF) (2)
•
(Reglas de inferencia de Armstrong)
Por ser X
superclave
Si X es clave candidata de R:
– XÆY (para todo subconjunto Y de R)
•
XÆY ⇒
/ YÆX
– DNIÆNombre_Pila frente a Nombre_PilaÆDNI
•
Las DF provienen de la semántica de los atributos
(universo del discurso)
•
Utilizaremos la siguiente representación gráfica de las
DF en una relación:
?
?
•
Ejemplo: {A→B, B→C} se puede inferir {A→C}
•
Se definen reglas de inferencia con el objetivo de
inferir DF de forma sistemática.
(R1) Reflexiva: Y ⊆ X ⇒ X→Y
A→A
ABC → AB
ABC → AC
(R2) Aumento: {X→Y} ⇒ XZ→YZ
A→A
A→C
BC → Z
CodAsig NomAsig CrT CrP Dpto NomDpto Dir Alum NomAlum Aula
¿Hay más DF?
ABC → ABC
AZ → CZ
BCD → ZD
(R3) Transitiva: {X→Y, Y→Z} ⇒ {X→Z}
A → BC
A→C
BC → Z
{CodAsig}Æ{NomAsig, CreT}
{NomAsig}Æ{CodAsig, CreT}
A→Z
{CodAsig, DNIAlum}Æ{Aula}
...
© A. Jaime, C. Domínguez 2005
DBD Tema 5
9
© A. Jaime, C. Domínguez 2005
DBD Tema 5
10
F+: Cierre del conjunto F de DF
Reglas de inferencia: de simplificación
(R4) Descomposición: {X→YZ} ⇒ {X→Y}
A → BC
A→B
BC→ ZXY
BC → X
BC → Z
•
Se llama cierre del conjunto F de DF, y se
representa con F+, al conjunto de DF que implica
lógicamente F.
•
Ejemplo:
EMPLEADO_DPTO
(R5) Unión o aditiva: {X→Y, X→Z} ⇒ {X→YZ}
A → BC
BC→ XY
BC → XYZ
BC → Z
NombEmp NSS FNcto Dirección NºDpto NomDpto NSSJefe
– F={NSSÆ{NomEmp, FNcto, Dirección, NºDpto},
NºDptoÆ{NomDpto, NSSJefe}}
– Por ejemplo se pueden inferir:
(R6) Pseudotransitiva: {X→Y, WY→Z} ⇒ {WX→Z}
A→B
BC→ ZXY
AC → ZXY
• NSSÆNSS
(R1)
• NSSÆ{NomDpto, NSSJefe}
(R3)
• NºDptoÆ NomDpto
(R4)
• NSSÆ{NomEmp, FNcto, Dirección, NºDpto,
NomDpto, NSSJefe}
(R5)
• ...
– F+ contiene a F y a todas las DF que se puedan
deducir.
© A. Jaime, C. Domínguez 2005
DBD Tema 5
11
© A. Jaime, C. Domínguez 2005
DBD Tema 5
12
X+: Cierre del cjto. de atributos X
bajo el cjto. F de DF
Superclave
Equivalencia de conjuntos de DF
•
X+ es el conjunto de atributos determinados
funcionalmente por X
•
El conjunto de atributos X es superclave si X+
incluye a todos los atributos del esquema de
relación.
•
Algoritmo para calcular X+ bajo el cjto. F de DF
//Reflexiva
X+←X
Mientras (haya algún cambio en X+)
Para cada DF (Y→Z) de F
Si Y ⊆ X+ entonces
X+ ← X+ ∪ Z //Transitiva
•
Ejemplo: R(ABCDEF)
•
{A}+ = {A, B, C, D, E, F}
{B}+ = {A, B, C, D, E}
A es superclave
B NO es superclave
•
E está cubierto por F si
– Toda DF de E está en F+
– O sea, toda DF de E se deduce de F
•
Para saber si F cubre a E
– Calcular X+ respecto a F, para cada DF XÆY
de E
– Comprobar que Y⊆X+
•
E es equivalente a F si
– E+ = F+
– O sea, si E cubre a F y viceversa
Ejemplo:
AlumAsig DNI Nom CódAsig NomAsig CrédT Aula
– F={ DNIÆNom,
{DNI,CódAsig}ÆAula
CódAsig Æ{NomAsig, crédT} }
– {DNI}+ = {DNI, Nom}
– {CodAsig}+ = {CódAsig, NomAsig, CrédT}
– {DNI,CodAsig}+ = {DNI, Nom, CódAsig,
NomAsig, crédT, Aula}
© A. Jaime, C. Domínguez 2005
DBD Tema 5
13
© A. Jaime, C. Domínguez 2005
Fmín ←F
El conjunto de DF F es mínimo si:
– Está en forma canónica: toda DF tiene un solo
atributo en la parte derecha
//Poner las DF en forma canónica:
– No contiene redundancias:
//Eliminar atributos redundantes de la izda
• Ninguna DF se puede inferir de las demás:
No se puede eliminar ninguna DF de F y
mantener el conjunto de DF equivalente a F
• Ninguna DF X→A
redundantes en X:
14
Algoritmo de cálculo de una
cobertura mínima Fmín
Conjunto F de DF mínimo
•
DBD Tema 5
tiene
atributos
No se puede sustituir una DF X→A de F por
otra Y→A donde Y⊂X y seguir teniendo un
conjunto de DF equivalente a F
Sustituir en Fmín cada X→{A1,...,An} por X→A1, ..., X→An
Para cada DF X→A de Fmín
Para cada atributo B∈X
Si Fmín–{X→A}∪{X–{B}→A} equivalente a Fmín
entonces Sustituir en Fmín X→A por X–{B}→A
//Eliminar las DF que se pueden inferir
Para cada DF X→A de Fmín
Si Fmín–{X→A} equivalente a Fmín entonces
Fmín ←Fmín –{X→A}
Ejemplo:
•
Cobertura mínima Fmín del conjunto F de DF:
conjunto de DF mínimo equivalente a F.
•
Un conjunto de DF puede tener varias coberturas
mínimas.
F={DNIÆNom, {DNI,CódAsig}Æ{Nom, Aula},
CódAsigÆ{NomAsig,crédT}, NomAsigÆcrédT}
Forma canónica: { DNIÆNom, {DNI,CódAsig}Æ Nom,
{DNI,CódAsig}ÆAula, CódAsigÆNomAsig,
CódAsigÆcrédT, NomAsigÆcrédT }
Atributos redundantes a la izquierda: {DNI,CódAsig}Æ Nom
DF que se pueden inferir: CódAsigÆcrédT
Fmín= {DNIÆNom, {DNI,CódAsig}Æ Aula,
CódAsigÆNomAsig, NomAsigÆcrédT }
© A. Jaime, C. Domínguez 2005
DBD Tema 5
15
© A. Jaime, C. Domínguez 2005
DBD Tema 5
16
Uso de DF para obtener claves candidatas
•
Partimos de un conjunto de DF mínimo donde obtenemos el
cierre de todas las partes izquierdas:
•
A B C D E F GH I
B+ • • • •
•
+
CD • • • •
•
+
E
• •
+
F
•
•
I+
• •
A B C D E F G H I
•
Uso de DF para obtener claves candidatas (2)
A B C D E F GH I
B+ • • • •
•
+
CD • • • •
•
+
E
• •
+
F
•
•
+
• •
B forma parte de I
una clave y CD
de otra clave
Los atributos que no estén en ninguna DF (columna sin puntos)
forman parte de todas las claves (H). Eliminar esas columnas:
A B C D E F GH I
B+ • • • •
•
+
CD • • • •
•
E+
• •
F+
•
•
I+
• •
•
•
Buscar columnas con mínimo número de puntos: el o los
atributos de la fila o filas forman parte de la clave:
•
H forma parte de
todas las claves
•
I y E forman parte
de todas las claves
•
A B C D E F GH I
B+ • • • •
•
+
CD • • • •
•
+
E
• •
+
F
•
•
I+
• •
•
Eliminar todas las columnas determinadas por los atributos de
esas filas
A B C D E F GH I
B+ • • • •
•
CD+ • • • •
•
+
E
• •
+
F
•
•
I+
• •
© A. Jaime, C. Domínguez 2005
DBD Tema 5
Descomposición
•
•
•
•
•
•
17
Aplicar repetidas veces los dos últimos pasos hasta que se
seleccionen todas las columnas:
Con esto se han
seleccionado
todas las
columnas
Las claves descubiertas son: HIEB y HIECD
Si alguna fila de las introducidas es determinada parcialmente
por otra DF, como ocurre con FÆC, donde C es parte de la fila
CD, entonces se puede sustituir, en las claves donde aparece, C
por F para obtener nuevas claves: HIEF
FD
Por lo tanto en nuestro caso encontramos tres claves: HIEB,
HIECD y HIEFD
Los pasos anteriores no conforman un algoritmo bien demostrado pero
ayudan a descubrir las claves en gran parte de los casos más
habituales.
Se pueden encontrar algoritmos demostrados formalmente en Saiedian
y otros Computer Journal 1996 y en Fadous y Forsyth ACM SIGMOD
1975
También existe una herramienta que acompaña al libro Diseño de BD
relacionales de Adoración de Miguel y otros, Ed. RAMA 1999
© A. Jaime, C. Domínguez 2005
DBD Tema 5
18
Descomposición conservando dependencias
Una descomposición de la relación R es un
conjunto de relaciones {R1, R2, .. Rn} que conserva
todos los atributos de R:
•
(proyección de R)
– Cada Ri = π<Atributos>R
– Cada atributo de R se encuentra en alguna Ri
•
Para cualquier extensión r de R se cumple:
r ⊆ r1 * r2 * r3 * … * rn (* es reunión natural)
•
Esto significa (“r⊆...” y no “r=...” ) que la reunión
natural de las proyecciones puede generar tuplas
espurias.
Necesitamos establecer una forma de comprobar
que la descomposición NO conlleva:
– La desaparición de DF
– La aparición de tuplas espurias
En la descomposición {R1,R2,...,Rn} de R
– F es el conjunto de DF de R
– Cada Ri tiene un conjunto de DF Fi
– Llamamos G=∪Fi
{R1,R2,...Rn} conserva las dependencias si F+=G+
Ejemplo 1: R1(A,B,C) y R2(D,E)
F2
F
F1
ABÆC
ABÆC
DÆE
DÆE
CÆD
G= ∪Fi
ABÆC
DÆE
¿CÆD puede inferirse a partir de G? NO, entonces
F+≠G+, luego NO se conservan las dependencias
•
Ejemplo 2:
F
ABÆC
CÆDE
ABÆF
EÆF
R1(A,B,C) y R2(C,D,E,F)
F1
ABÆC
F2
CÆDE
EÆF
G= ∪Fi
ABÆC
CÆDE
EÆF
¿ABÆF puede inferirse a partir de G? SI, entonces
F+=G+, luego SÍ se conservan las dependencias
© A. Jaime, C. Domínguez 2005
DBD Tema 5
19
© A. Jaime, C. Domínguez 2005
DBD Tema 5
20
Descomposición conservando dependencias (2)
Descomposición sin pérdidas (o no aditiva)
•
•
Ejemplo3:
F
ABÆC
CÆDE
R1(A,B,C,D) y R2(C,E)
F2
F1
G= ∪Fi
ABÆC
CÆD
ABÆC
CÆD
CÆE
•
Ejemplo 4:
F
CÆE
F+=G+,
ABÆC
ABÆC
•
•
¿CDÆE puede inferirse a partir de G? NO, entonces
F+≠G+, luego NO se conservan las dependencias
© A. Jaime, C. Domínguez 2005
DBD Tema 5
r = r1 * r2 * r3 * … * rn (* es reunión natural)
–
Eso significa que no se generan tuplas espurias
21
Ejemplo de descomposición CON pérdidas:
–
R(A,B,C,D,E,F)
–
F= {ABÆD, ACÆE, ABDÆF}
–
Descomposición R1(A,B,D,F), R2(A,C,E)
•
No se pierden DF, pero se parte el trío ABC.
•
R1*R2 puede generar tuplas espurias
{R1, R2} es una descomposición sin pérdidas de R si
y sólo si al menos una de estas dos DF aparece en F+,
siendo F el conjunto de DF de R :
–
R1 ∩ R2 → R1
–
R1 ∩ R2 → R2
© A. Jaime, C. Domínguez 2005
Descomposiciones sucesivas sin pérdidas
Los atributos de reunión
natural (R1∩R2) son bien
superclave de R1 o de R2
DBD Tema 5
22
Proceso de normalización
•
Si {R1,...,Ri,...,Rn} es una descomposición sin
pérdidas (DSP) de R
•
•
•
Si además {Q1,...,Qk}es una DSP de Ri
Entonces la descomposición
{R1,...,Ri-1,Q1,...,Qk,Ri+1,...,Rn}
será también una DSP
•
•
•
Sabemos
que es una
DSP
–
(por eso se llama también “no aditiva”)
luego SÍ se conservan
las dependencias
G= ∪Fi
ABÆC
CDÆE
R si para cualquier extensión r de R se cumple:
ABÆC
CÆD
CÆE
R1(A,B,C) y R2(D,E)
F2
F1
{R1,R2,...Rn} es una descomposición sin pérdidas de
Sabemos
que es una
DSP
Descomposición de esquemas de relación
insatisfactorios
Repartiendo sus atributos entre otros esquemas de
relación más pequeños
Estos otros esquemas poseen propiedades deseables:
menos anomalías de actualización
La descomposición debe :
– Conservar los atributos
Definición de
descomposición
– Conservar las dependencias funcionales (se
Descomposición sin
pérdidas (no aditiva)
sacrifica a veces)
– Evitar el problema de las tuplas espurias
•
Podemos garantizar que la sucesión
de ambas descomposiciones
también es DSP
Es preferible partir de una cobertura mínima
Relación
normalizada
Buen
diseño
Llegar a la
FN más alta
Hay que considerar
el rendimiento
© A. Jaime, C. Domínguez 2005
DBD Tema 5
23
© A. Jaime, C. Domínguez 2005
DBD Tema 5
24
Conceptos del modelo relacional
Primera forma normal (1FN)
•
X
R
Esquema
de relación
Una relación R está en 1FN si
– Todos sus atributos son monovaluados
Conjunto de
atributos
Multivaluado
DNI
•
X es superclave de R si X → R
•
X es clave candidata de R si es superclave mínima:
– X superclave
– ∀ Y∈X, X-Y no es superclave
Nom
(Imposible en
relacional)
Tfnos
Persona
DNI Nom Tfnos
PERSONA
•
Clave primaria de R: es una concreta entre las
candidatas
•
Atributo primo: es aquel que forma parte de alguna
clave candidata
•
Atributo NO primo: es el que no figura en ninguna
clave candidata
SOLUCIÓN:
Persona’
Tfnos
DNI Nom
DNI Tfno
Sin pérdidas:
Persona’∩Tfnos
→Persona’
Se mantiene de alguna manera:
todos los tfnos asociados a un
DNI aparecen en algún par con
ese DNI
SOLUCIONES CON INCONVENIENTES:
Persona
DNI Nom Tfno
Redundancia de tuplas.
A descomponer después
Máximo 3
valores
Puede incluir
muchos valores
nulos
Persona
DNI Nom Tfno_1 Tfno_2 Tfno_3
Primo: traducción del inglés prime. Otros libros lo traducen por
atributo “principal”
© A. Jaime, C. Domínguez 2005
DBD Tema 5
25
© A. Jaime, C. Domínguez 2005
Segunda forma normal (2FN)
•
•
DBD Tema 5
26
2FN: Ejemplos
X→Y es total, si eliminando cualquier atributo de X,
la DF deja de ser válida: ¬∃ z∈X, X-z→Y
DF parcial
Clave única:
{NSS, NºProy}
no primo
X→Y es DF parcial, si quitando algún atributo de X
la DF sigue siendo válida: ∃ z∈X, X-z→Y
no primo
NSS NºProy Horas NomEmp NomPry LugarPry
no primo
•
•
NO figura
en ninguna
clave
candidata
La relación R está en 2FN si y sólo si:
– Está en 1FN
– Todo atributo no primo depende funcionalmente
de manera total de toda clave de R (primaria o
candidata)
SOLUCIÓN:
– Las DF parciales se llevan a nuevas tablas
– En la tabla original queda la clave y los atributos
que dependan totalmente de ella
Clave única: AB
R
A B C D E
R1
R2
A B C E
B D
DF parcial
NSS NºProy Horas
•
NSS NomEmp
NºProy NomPry LugarPry
Si hay DF parciales con una clave candidata se
resuelve de la misma forma:
Clave candidata: BC
D no primo
R1 A B C
R A B C D
R2 C D
DF parcial de
clave candidata
D no primo
DF parcial de clave primaria
© A. Jaime, C. Domínguez 2005
DBD Tema 5
Sin pérdidas:
R1∩R2→R2
27
© A. Jaime, C. Domínguez 2005
DBD Tema 5
28
2FN: anomalías corregidas
Tercera forma normal (3FN)
Clave única:
{CódTienda, CodProd}
•
DF parcial
Ventas
CódTienda CódProd Precio Unidades SuminisDirSum
Ventas’
CódTienda CódProd Unidades
•
•
•
•
Una relación R está en 3FN si y sólo si:
– Está en 2FN
– Para toda DF X → Y de R:
• X es superclave o bien Y es atributo primo
Producto
CódProd Precio SuminisDirSum
Actualizar precio de un producto Ö modificar 1 tupla
Insertar nuevo producto
Ö se conoce toda la clave de la nueva tupla: PROD4
Borrar una venta
Ö no se pierde información de ningún Producto
Esto supone que no hay
dependencias transitivas
respecto a claves candidatas
A→X (X→A)
X→Y y A clave candidata
•
Producto está en 2FN, pero ...
SOLUCIÓN:
– R(A,X,Y,B) donde X → Y incumple 3FN
– Crear otra relación con X+, con X como clave
– Eliminar Y de R
Claves: A
Producto
CódProd Precio Suminis DirSum
DVD_20
40
ACR Barcelona
TV_100
80
Altus
Teruel
CAD_9
80
ACR Barcelona
C_VID_3 360
ACR Barcelona
R1 A X B
R A X Y B
R2 X Y
– Actualizar DirSum de un suministrador conlleva
modificar varias tuplas
© A. Jaime, C. Domínguez 2005
DBD Tema 5
29
X no
superclave
© A. Jaime, C. Domínguez 2005
3FN: Ejemplos
Asignatura
no superclave
Y no
primo
Sin pérdidas:
R1∩R2→R2
DBD Tema 5
30
3FN: anomalías corregidas
no primo
Producto
CódProd Precio SuminisDirSum
no primo
COD_ASG NOM_ASG CRED DPTO NOM_DPTO DIR_DPTO
Asignatura’
COD_ASG NOM_ASG CRED DPTO
Producto’
CódProdPrecio Suminis
Suministrador
Suminis DirSum
•
Actualizar DirSum de un suministrador Ö modificar
1 tupla
•
Sin embargo, en el siguiente caso, donde:
ASIG
N
Departamento
1
DPTO NOM_DPTO DIR_DPTO
Claves:
Id y
{Localidad,
CódParcela}
transitiva
– En cada tienda, cada producto es vendido por un único
suministrador
– Cada suministrador distribuye un solo producto
– Un mismo producto puede venderse en varias tiendas
DPTO
Suministro
CódTienda CódProd Suministrador
Claves:
{CódTienda, CódProd} y
{CódTienda,Suministrador}
no superclave
Id Localidad CódParcela Área Precio
no primo
•
Suministro está en 3FN, pero ...
Suministro
CódTienda CódProd Suministrador
Eroski
Prod1
ACME
Eroski
Prod2
PTT
Carrefour Prod1
ACME
Carrefour Prod5
ATT
Id Localidad CódParcela Área
© A. Jaime, C. Domínguez 2005
DBD Tema 5
Área Precio
– Borrar las tuplas de Eroski conlleva eliminar
también que PTT suministra Prod2
31
© A. Jaime, C. Domínguez 2005
DBD Tema 5
32
Forma normal de Boyce-Codd (FNBC)
FNBC: ejemplos
Claves: A,
BC y BD
•
Una relación R está en FNBC si y sólo si:
– Está en 3FN
– Para toda DF X → Y de R X es superclave
R1 A B D
R A B C D
C primo
•
SOLUCIÓN:
R2 D C
D no superclave
R1 C B
R A B C
Claves:
AB y AC
R2 A C
B es
C no
primo
superclave
Claves: AB,
EF, AF y CF
Sin pérdidas:
R1∩R2→R1
C no superclave
•
•
•
E primo
En ocasiones se pierde alguna DF ({A,B}→C)
Entonces habrá que replantearse cuál es la clave de R2:
probablemente la combinación de atributos de R2
R A B C D E F
SOLUCIONES CON INCONVENIENTES:
B primo
R1 A B
R2 A C
R1 C B
R2 A B
© A. Jaime, C. Domínguez 2005
R2 F B
F no superclave
DBD Tema 5
33
© A. Jaime, C. Domínguez 2005
DBD Tema 5
Transitiva:
{CIF, CódRes}ÆId,
IdÆ{GrToxic, Localidad}
Id CIF CódRes GrToxic Localidad JefeLab
Suministro
CódTienda CódProd Suministrador
Suministro_2
Id
1
2
3
4
5
6
7
8
9
10
CódTienda Suministrador Suministrador CódProd
Suministro_1
CódTienda Suministrador
Eroski
ACME
Eroski
PTT
Carrefour
ACME
Carrefour
ATT
CIF CódRes GrToxic Localidad JefeLab TítuloJefe
E1
H1
5
Logroño
Eloy Dr. Química
E1
H2
7
Calahorra
Eloy Dr. Química
E2
H1
3
Arnedo
Marta
Ingeniero
E3
H3
4
Haro
Javier
Ingeniero
E3
H4
1
Haro
Javier
Ingeniero
E3
H5
3
Haro
Javier
Ingeniero
E4
H1
1
Ezcaray
Irene
Dr. física
E4
H2
7
Ezcaray
Irene
Dr. física
E4
H7
10
Anguiano Irene
Dr. física
E4
H3
1
Anguiano Irene
Dr. física
{CIF,CódRes}+
Id+
CIF+
Localidad+
JefeLab+
Borrar las tuplas de Eroski ya no elimina que PTT
suministra Prod2
•
•
DBD Tema 5
TítuloJefe
Id
CIF
CódRes
GrToxic
Localidad
JefeLab
TituloJefe
Suministro_2
Suministrador CódProd
ACME
Prod1
PTT
Prod2
ATT
Prod5
© A. Jaime, C. Domínguez 2005
34
Normalización: ejemplo (1)
Claves: {CódTienda, CódProd}
y {CódTienda, Suministrador}
•
R3 C E
También pierden {A,B}→C
Generan tuplas espurias
FNBC: anomalías corregidas
Suministro_1
R1 A F C D
35
• • • • • • •
• • • • • • •
•
• •
•
• • •
• •
LocalidadÆCIF
Claves candidatas: Id, {CIF,CódRes},
{Localidad, CódRes}
Atributos no primos:GrToxic, JefeLab,TítuloJefe
© A. Jaime, C. Domínguez 2005
DBD Tema 5
36
Normalización: ejemplo (2)
Normalización: ejemplo (3)
no superclave
Id CIF CódRes GrToxic Localidad JefeLab
no superclave
TítuloJefe
Id CIF CódRes GrToxic Localidad
CIF JefeLab TítuloJefe
Parcial sobre
no primo
no primo
3FN
Primo: en 3FN
2FN
CIF JefeLab JefeLab TítuloJefe
CIF JefeLab TítuloJefe
Id CIF CódRes GrToxic Localidad
Id
1
2
3
4
5
6
7
8
9
10
•
•
CIF CódRes GrToxic Localidad
E1
H1
5
Logroño
E1
H2
7
Calahorra
E2
H1
3
Arnedo
E3
H3
4
Haro
E3
H4
1
Haro
E3
H5
3
Haro
E4
H1
1
Ezcaray
E4
H2
7
Ezcaray
E4
H7
10
Anguiano
E4
H3
1
Anguiano
CIF JefeLab TítuloJefe
E1 Eloy Dr. Química
E2 Marta
Ingeniero
E3 Javier
Ingeniero
E4 Irene
Dr. física
•
•
Clave candidata:
CIF
Atributos no primos:
JefeLab, TítuloJefe
Id
1
2
3
4
5
6
7
8
9
10
CIF CódRes GrToxic Localidad
E1
H1
5
Logroño
E1
H2
7
Calahorra
E2
H1
3
Arnedo
E3
H3
4
Haro
E3
H4
1
Haro
E3
H5
3
Haro
E4
H1
1
Ezcaray
E4
H2
7
Ezcaray
E4
H7
10
Anguiano
E4
H3
1
Anguiano
•
Claves candidatas: Id,
{CIF,CódRes}, {Localidad,CódRes}
Atributos no primos:GrToxic
•
•
Claves candidatas: Id,
{CIF,CódRes}, {Localidad,CódRes}
Atributos no primos:GrToxic
© A. Jaime, C. Domínguez 2005
CIF JefeLab
E1 Eloy
E2 Marta
E3 Javier
E4 Irene
• Clave candidata:
CIF
• Atributo no primo:
JefeLab
JefeLab TítuloJefe
Eloy Dr. Química
Marta
Ingeniero
Javier
Ingeniero
Irene
Dr. física
•
DBD Tema 5
37
© A. Jaime, C. Domínguez 2005
Normalización: ejemplo (4)
Clave candidata:
JefeLab
Atributo no primo:
TítuloJefe
DBD Tema 5
38
Desnormalización
CIF JefeLab
•
Id CIF CódRes GrToxic Localidad
JefeLab TítuloJefe
Objetivo: Introducción de redundancia de forma
controlada para mejorar la eficiencia del sistema:
– Para consultas frecuentes
FNBC
– Ejemplo: evitar ejecutar reuniones (join)
no superclave
Ambas en FNBC
Localidad CIF
Id Localidad CódRes GrToxic
Id
1
2
3
4
5
6
7
8
9
10
Localidad CódRes GrToxic
Logroño
H1
5
Calahorra
H2
7
Arnedo
H1
3
Haro
H3
4
Haro
H4
1
Haro
H5
3
Ezcaray
H1
1
Ezcaray
H2
7
Anguiano
H7
10
Anguiano
H3
1
© A. Jaime, C. Domínguez 2005
Se pierde algo de normalización
•
REGLA de oro para desnormalizar:
– Considerarlo sólo si el comportamiento no es
satisfactorio, la relación tiene una tasa de
actualización pequeña y una tasa de consultas alta
Localidad CIF
Logroño E1
Calahorra E1
Arnedo E2
Haro
E3
Ezcaray E4
Anguiano E4
•
Caso 1º: Combinar tablas con asociación 1:1
Estudiante 1
CIF JefeLab
E1 Eloy
E2 Marta
E3 Javier
E4 Irene
Estudiante
0..1 Proyecto
Estudiante_Proyecto
Proyecto
JefeLab TítuloJefe
Eloy Dr. Química
Marta
Ingeniero
Javier
Ingeniero
Irene
Dr. física
DBD Tema 5
•
39
– Si se accede frecuentemente a las tablas juntas
– Si se accede raramente a las tablas por separado
– Si hay pocos valores nulos (es decir, estudiantes
sin proyecto)
© A. Jaime, C. Domínguez 2005
DBD Tema 5
40
Desnormalización (2)
•
Caso 2º: Duplicar atributos no primos en asociaciones 1:N
A
–
–
–
–
–
•
*
A A1 A2 A3 A4
B
*
Caso 3º: Duplicar claves extranjeras en asociaciones 1:N
A * 1
Caso 4º: Duplicar atributos en asociaciones M:N
A
1
Atributo
B B1 B2 A1 A3
redundante
CE
Si el atributo duplicado (A3) se actualiza rara vez
Si las consultas que usan B y A3 son frecuentes
(se ahorra una reunión)
Cada modificación de A3 en A supone cambiarlo
en todos los B relacionados
Al borrar en A hay que cambiar A1 y A3 en B
Precisa más espacio (valores duplicados)
B
•
Desnormalización (3)
B * 1 C
1
*
A A1 A2 B1 C1
CE CE
B B1 B2 C1
CE
C C1 C2
– Para relacionar los A con C se ahorra una reunión
– Se crea una nueva restricción FOREIGN KEY...
– Precisa más espacio
© A. Jaime, C. Domínguez 2005
DBD Tema 5
41
*
A A1 A2 A3 A4
B B1 B2 B3 B4
AB A1 B1 A4 B4
CE CE
Atributos redundantes
– Evita la reunión de AB con A y B para acceder a A4
o B4
– Si A4 o B4 aparecen en muchas consultas sobre AB
pero sin necesidad de usar otros atributos de A o B
– Cambios de A4 en A o de B4 en B, supondrán
muchas modificaciones en AB
•
Caso 5º: Atributos multivaluados
A
A1
A2[0..3]
A A1 A2_1 A2_2 A2_3
– Si el número máximo de valores es pequeño y
conocido y no cambia a lo largo del tiempo
– Algunos SGBD dan la posibilidad de usar arrays
– No conviene que se originen demasiados nulos
– Las consultas esperadas no deberían ser complicadas
© A. Jaime, C. Domínguez 2005
DBD Tema 5
42
Otros refinamientos
•
Caso 6º: Datos derivados
– ¿Almacenar un dato o calcularlo?
– Ejemplo: Salario total de cada departamento
– A tener en cuenta:
• Ahorro de espacio para almacenar datos
• Costo de mantenimiento de la consistencia de los
datos derivados frente al de calcular el dato derivado
cada vez que se necesita
•
Caso 7º: Tablas extracto
– Para datos costosos de conseguir (con vista materializada)
– La actualidad al minuto no es imprescindible (puede valer
la de ayer): la tabla extracto se actualiza periódicamente
(cada día o cada semana, ...)
– La tabla extracto contiene los datos para ser usados
•
Caso 8º: Lista de elementos
Inmueble’
Tipo
Cód Calle CP Tipo Tipo Descr
Ejercicios
Inmueble
Cód Calle CP Tipo Descr
1=casa, 2=apartamento, 3=estudio, ...
– La tabla Tipo contiene las opciones disponibles. El atributo
Tipo ocupa menos que descr. La descr sólo se modifica en
un sitio
– Si es frecuente el JOIN entre tipo e Inmueble, podemos
incluirlo directamente en la tabla Inmueble
© A. Jaime, C. Domínguez 2005
DBD Tema 5
43
© A. Jaime, C. Domínguez 2005
DBD Tema 5
44
Ejercicios: identificar dependencias
funcionales
•
1)
Ejercicios: Cierre de conjunto de atributos
y cobertura mínima
Descubrir todas las posibles DF en cada uno de los
siguientes esquemas de relación:
PERSONA
Calcula el cierre de conjunto de atributos para cada
parte izquierda de cada DF:
1) F={B→{A, C, D, E}, E→{F, G}}
2) F={A→B, C→{D, E}, {A, C}→F}
3) F={A→B, B→{C, D}, {A, C}→F, {D, F}→G}
DNI Nombre Apellidos Edad Zona ...
... Calle NºBloque Planta Puerta
2)
•
CUENTA
•
NºBanco NomBanco NºSucursal Ciudad ...
Calcula una cobertura mínima para cada uno de los
siguientes conjuntos de DF:
Saldo DNI_Titular ...
...
... Dirección NºCta Interés
TfnoTitular
...
... DirTitular
1) F={A→B, C→E, C→{D, E}, {A, C}→F, {A,
C}→ {A, D, E}, {A, C, D}→B}
Hay que tener en cuenta que el número de cuenta
completo incluye el código de banco, el de sucursal
y el nº de cuenta
3)
2) F={A→B, B→{C, D}, {A,F}→{B,F}, {A,
C}→F, {D, F}→G, {A, B}→{C, D}, {F,G}→G,
A→D}
EMPLEADO_DPTO
NombreEmp NSS FechaNcto Dirección NºDpto ...
... NombreDpto NSSJefeDpto
4)
EMPLEADO_PROY
NSS NºProy Horas NombreEmp ...
... NombreProy LugarProy
© A. Jaime, C. Domínguez 2005
DBD Tema 5
45
Ejercicios: Comprobación de descomposición
que conserva DF y es sin pérdidas
R1 A D C
© A. Jaime, C. Domínguez 2005
1)
R2 A B E
R1 A B C
R2 C D E
R1 A B D
R2 A B C E
R1 A B C D E
R2 B F G H R3 D I J
R1 A B C
R3 B F
R5 D I J
6)
A B C D E F G
7)
A B C D E F
A B C D E F G H I J
R2 A D E
R4 F G H
3)
8)
A B C D E F G H I J
A B C D E F G H I J K
R1 A B C D R2 D E
R3 B F
R4 F G H
R5 D I J
9)
4)
R1 A B C D E ...
... F G
3) R A B C D E F G H I J K L M N O
A B C D E F
2)
R1 A B C D R2 C E
2) R A B C D E F G H I J
46
Ejercicios: Cálculo de claves candidatas y
obtención de 2FN, 3FN y FNBC
R1 A B C D R2 A B E
1) R A B C D E
DBD Tema 5
A B C D E F G H I J
A B C D E F
R2 A H I J K ...
... L M N O
R1 A B C D E ...
... F G N O
5)
A B C D E F G H I J K L MN O
R2 C D L M
R1 A B C D E F G H I J K L M
R2 A B C D E F G M N O
© A. Jaime, C. Domínguez 2005
DBD Tema 5
R3 H I J K B
47
© A. Jaime, C. Domínguez 2005
DBD Tema 5
48
Ejercicios: Cálculo de claves candidatas y
obtención de 2FN, 3FN y FNBC (2)
10)
NomAsig Dpto CrédsCurso DNIProf Cuatr Año Horario Aula ...
... NºAlumnos
© A. Jaime, C. Domínguez 2005
DBD Tema 5
49