Cadenas de Markov

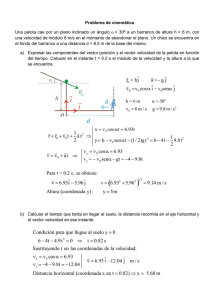
Probabilidad condicional - CADENAS DE MARKOV
2.3
CADENAS DE MARKOV
Procesos estocásticos
Supóngase que una oficina de negocios tiene cinco líneas telefónicas y que en un
instante de tiempo dado puede haber un número cualquiera de líneas ocupadas. Durante
un periodo de tiempo se observan las líneas telefónicas a intervalos regulares de 2
minutos y se anota el número de líneas ocupadas en cada momento. Sea X1 el número
de líneas ocupadas cuando se observan al principio del periodo; sea X2 el número de
líneas ocupadas cuando se observan en el segundo instante de tiempo, 2 minutos
más tarde; y en general, para n = 1,2,..., sea Xn el número de líneas ocupadas cuando
se observan en el instante de tiempo n-ésimo.
La sucesión de observaciones X1, X2 ...., se denomina proceso estocástico, o proceso aleatorio, porque los valores de estas observaciones no se pueden predecir
exacta-mente de antemano, pero se pueden especificar las probabilidades para los
distintos valores posibles en cualquier instante de tiempo. Un proceso estocástico como
el que se acaba de describir se llama proceso de parámetro discreto, ya que las líneas
se observan solamente en puntos discretos o separados en el tiempo, en lugar de
continuamente en el tiempo.
En un proceso estocástico la primera observación X1 se denomina estado inicial
del proceso y para n = 2, 3,..., la observación Xn se denomina estado del proceso
en el instante de tiempo n. En el ejemplo anterior, el estado del proceso en cualquier
instante de tiempo es el número de líneas que están siendo utilizadas en ese instante.
Por tanto, cada estado debe ser un entero entre 0 y 5. En el resto del capítulo se
considerarán únicamente procesos estocásticos para los cuales sólo existe un número
finito de estados posibles en cualquier tiempo determinado.
En un proceso estocástico de parámetro discreto, el estado del proceso varía
aleatoriamente en cada instante. Para describir un modelo de probabilidad
completo para un proceso, es necesario especificar una probabilidad para cada uno
de los valores posibles del estado inicial X1 y especificar también, para cada uno de
los sucesivos estados xn+1 (n = 1,2,...), la siguiente probabilidad condicional:
Pr(Xn +1 = x n+1 │X 1 = x 1 ,X 2 = x 2 ,... ,X n = x n ).
En otras palabras, para cada instante de tiempo n, el modelo de probabilidad
debe especificar la probabilidad condicional de que el proceso esté en el estado
x n+1 en el tiempo n + 1, dado que en los instantes de tiempo 1,..., n el
proceso estaba en los estados, x 1 ... X n .
Cadenas de Markov
Definición. Una cadena de Markov es un tipo especial de proceso estocástico,
que se puede describir como sigue: En cualquier instante de tiempo n dado,
cuando el estado actual Xn y todos los estados previos X1,..., Xn-1 del proceso
son conocidos, las probabilidades de los estados futuros Xj (j > n) dependen
solamente del estado actual Xn y no dependen de los estados anteriores X1,... ,
Xn-1. Formalmente, una cadena de Markov es un proceso estocástico tal que
para n = 1,2,... y para cualquier sucesión posible de estados xi,x2 , ...,x n + i,
Pr( X n+1 = x n+1 │X 1 = x 1 , X 2 = x 2 ,..., X n = x n ) = Pr(X n+1 = x n+1 │X n = x n ) .
Probabilidad y Estadística
Probabilidad condicional - CADENAS DE MARKOV
Utilizando la regla de la multiplicación para probabilidades condicionales
presentada en la sección 2.1 se deduce que las probabilidades de una cadena de
Markov deben satisfacer la relación
Pr(X 1 = x 1 , X 2 = x 2 ,... ,X n = x n ) = Pr( X 1 = x 1 ) Pr( X 2 = x 2 │X 1 = x 1 ) =
Pr(X 3 = x 3 │X 2 = x 2 ).. Pr ( X n = x n |X n-1 = x n-1 )
Cadenas de Markov finitas con probabilidades de transición estacionarias. Se
considerará ahora una cadena de Markov para la cual existe sólo un número finito k
de estados posibles s1,..., Sk y en cualquier instante de tiempo la cadena debe estar
en uno de estos k estados. Una cadena de Markov de este tipo se denomina
cadena de Markov finita. La probabilidad condicional Pr(Xn+1 = sj │Xn = si) de
que la cadena de Markov esté en el estado sj en el instante de tiempo n + 1 si está
en el estado s, en el instante de tiempo n se denomina probabilidad de transición.
Si para una cadena de Markov esta probabilidad de transición tiene el mismo valor
para todos los instantes de tiempo n (n = 1,2,...), se dice que la cadena de Markov
tiene probabilidades de transición estacionarias. En otras palabras, una cadena de
Markov tiene probabilidades de transición estacionarias si, para cualquier par de
estados si y sj, existe una probabilidad de transición pij tal que
Pr (X n + 1 = s j \ X n = si) = pij
para n = 1 , 2 , . . .
Para ilustrar la aplicación de estas definiciones se considerará de nuevo el
ejemplo de la oficina con cinco líneas telefónicas. Para que este proceso estocástico
sea una cadena de Markov, la probabilidad de cada posible número de líneas
ocupadas en cualquier instante de tiempo deben depender solamente del número
de líneas que estaban ocupadas cuando el proceso fue observado 2 minutos antes y
no debe depender de ninguno de los otros valores observados obtenidos
previamente. Por ejemplo, si en el instante de tiempo n había tres líneas
ocupadas, entonces la probabilidad especificada para el instante de tiempo n + 1
debe ser la misma, con independencia de si estaban ocupadas 0, 1, 2, 3, 4 ó 5
líneas en el instante de tiempo n — 1. En realidad, sin embargo, la observación
en el instante de tiempo n — 1 podría proporcionar información sobre el tiempo
que cada una de las tres líneas en uso en el instante de tiempo n había estado
ocupada y esta información podría ser útil para determinar la probabilidad en
el instante de tiempo n + 1. No obstante, se supone que este proceso es una
cadena de Markov. Si esta cadena de Markov ha de tener probabilidades de
transición estacionarias, debe verificarse que la proporción entre llamadas
telefónicas entrantes y salientes y el promedio de duración de las mismas no
cambie durante el periodo cubierto por el proceso. Este requisito significa que el
periodo completo no puede incluir intervalos de tiempo densos en que se
esperan más llamadas o intervalos de tiempo tranquilos en qué se esperan pocas
llamadas. Por ejemplo, si en un instante de tiempo, sea cual sea, sólo hay una
línea ocupada, entonces debe haber una probabilidad específica p1j de que 2
minutos más tarde exactamente j líneas estén en uso.
Probabilidad y Estadística
Probabilidad condicional - CADENAS DE MARKOV
Matriz de transición
Matriz de transición para un sólo paso. Considérese una cadena de Markov
con k estados posibles s1,..., sk y probabilidades de transición estacionarias.
Para i = 1,..., k y j = 1,..., k, se denota de nuevo por pij la probabilidad
condicional de que el proceso esté en el estado sj en un instante de tiempo si está
en el estado si, en el instante anterior. La matriz de transición de la cadena de
Markov se define como la matriz k x k P con elementos pij Por tanto,
P =
p 11 … p 1k
p21 … p2k
…………….
pk1 … pkk
(1)
Probabilidad y Estadística
Probabilidad condicional - CADENAS DE MARKOV
Una matriz cuadrada cuyos elementos son no negativos y en la que la suma de
los elementos de cada fila es 1 se denomina matriz estocástica. Resulta pues
que la matriz; transición P de cualquier cadena de Markov finita con
probabilidades de transición estacionarias debe ser una matriz estocástica.
Inversamente, cualquier matriz estocástica x k puede servir como la matriz de
transición de una cadena de Markov con k estados posibles y probabilidades de
transición estacionaria.
Ejemplo 1: Matriz de transición para el número de líneas telefónicas ocupadas.
Supóngase que en el ejemplo de la oficina con cinco líneas telefónicas los
números de líneas que están siendo utilizadas en los instantes de tiempo 1,2,...
constituyen una cadena de Markov con probabilidades de transición
estacionarías. Esta cadena tiene seis estados posibles b0, b1, … b5, donde bi, es el
estado en el que se están utilizando exactamente i líneas en un instante de tiempo
determinado (i = 0,1,..., 5). Supóngase que la matriz de transición P es la
siguiente:
(a) Suponiendo que las cinco líneas están ocupadas en un instante de tiempo
concreto, se determinará la probabilidad de que en el siguiente instante de
tiempo haya exactamente cuatro líneas ocupadas, (b) Suponiendo que en un
instante de tiempo no hay ninguna línea ocupada, se determinará la probabilidad
de que en el instante de tiempo siguiente haya al menos una línea ocupada.
(a) Esta probabilidad es el elemento de la matriz P en la fila
correspondiente al estado 65 y la columna correspondiente al estado b4. Se
observa que este valor es 0.4.
(b) Si en un instante de tiempo no hay ninguna línea ocupada, entonces el
elemento de la esquina superior izquierda de la matriz P proporciona la
probabilidad de que en el instante siguiente no haya ninguna línea ocupada. Se
observa que este valor es 0.1.
Por tanto, la probabilidad de que en el siguiente instante de tiempo se esté
utilizando al menos un línea es 1 - 0.1 = 0,9.
Matriz de transición para varios pasos. Considérese de nuevo una cadena de
Markov arbitraría con k estados posibles s1,..., sk y la matriz de transición P de
la ecuación (1) y supóngase que la cadena está en el estado si en un instante de
tiempo n. Se determinará ahora la probabilidad de que la cadena esté en el estado
sj en el instante de tiempo n + 2. En otras palabras, se determinará la probabilidad
de que la cadena pase del estado s¡ al estado sj en dos pasos. La notación para
esta probabilidad es
Para n = 1,2,..., sea Xn el estado de la cadena en el instante de tiempo n.
Entonces, si sr representa el estado al que ha pasado la cadena en el instante de
tiempo n + 1,
Probabilidad y Estadística
Probabilidad condicional - CADENAS DE MARKOV
Ejemplo 2: Matrices de transición de dos y tres pasos para el número de líneas
telefónicas ocupadas. Considérese nuevamente la matriz de transición P de la
ecuación (2) para la cadena de Markov basada en cinco líneas telefónicas.
Supóngase en primer lugar que en un instante de tiempo hay i líneas ocupadas y
se determinará la probabilidad de que dos instantes de tiempo después haya
exactamente j líneas ocupadas.
Si se multiplica la matriz P por sí misma, se obtiene la siguiente matriz de
transición de dos pasos:
A partir de esta matriz se puede calcular cualquier probabilidad de transición de
dos pasos le la cadena como sigue:
(1) Si dos líneas están ocupadas en un instante de tiempo concreto, entonces la
probabilidad de que dos instantes después haya cuatro líneas ocupadas es
0.17.
(2) Si en un instante de tiempo hay tres líneas ocupadas, entonces la probabilidad
de que dos instantes después haya de nuevo tres líneas ocupadas es 0.20.
Supóngase ahora que i líneas están ocupadas en un instante de tiempo
concreto y se determinará la probabilidad de que tres instantes después haya
exactamente j líneas ocupadas.
S¡ se calcula la matriz P3 = P2P, se obtiene la siguiente matriz de
transición de tres pasos:
Probabilidad y Estadística
Probabilidad condicional - CADENAS DE MARKOV
S¡ se calcula la matriz P3 = P2P, se obtiene la siguiente matriz de
transición de tres pasos:
A partir de esta matriz se puede calcular cualquier probabilidad de transición de
tres pasos para la cadena como sigue:
(1) Si las cinco líneas están ocupadas en un instante de tiempo, entonces la
probabilidad de que no haya líneas ocupadas tres instantes después es
0.116.
(2) Si una línea está ocupada en un instante de tiempo, entonces la probabilidad
de que tres instantes después haya de nuevo exactamente una línea ocupada
es 0.207.
Vector de probabilidades iniciales
Supóngase que una cadena de Markov finita con probabilidades de transición
estacionarias tiene k estados posibles s1,..., sk y que la cadena puede estar en
cualquiera de estos k estados en el tiempo de observación inicial n = 1.
Supóngase también que, para i = 1,..., k, la probabilidad de que la cadena esté
en el estado s, al inicio del proceso es vi, donde vi ≥ 0 y vi +… + vk. = 1.
Cualquier vector w = ( w 1 , . . . , w k ) tal que w i ≥ 0 para i = 1,..., k y
también
wi = 1 se denomina vector de probabilidades.
El vector de probabilidades v = (v1 , ..., vk), que especifica las
probabilidades de diversos estados de la cadena en la observación inicial de
tiempo, se denomina vector de probabilidades iniciales de la cadena.
El vector de probabilidades iniciales y la matriz de transición determinan la
probabilidad de que la cadena esté en un estado en un instante de tiempo. Si v es
el vector de probabilidades iniciales de la cadena, entonces Pr(X 1 = s¡) = v i ,
para i = 1,... , k . Si la matriz de transición de la cadena es la matriz k x k P de
elementos p¡j que se indica en la ecuación (1), entonces para j = 1,..., k,
Probabilidad y Estadística
Probabilidad condicional - CADENAS DE MARKOV
Puesto que
es la componente j-ésima del vector vP, resulta que las
probabilidades para el estado de la cadena en el segundo instante de tiempo se
especifican por el vector de probabilidades vP.
En general, supóngase que en un instante de tiempo n la probabilidad de que
la cadena esté en el estado si es Pr(Xn = si) = wi, para i = 1,..., k. Entonces,
En otras palabras, si las probabilidades de los diversos estados en el instante de
tiempo n se especifican por el vector de probabilidades w, entonces las probabilidades
en el instante de tiempo n + 1 se especifican por el vector de probabilidades wP.
Resulta pues que si el vector de probabilidades iniciales para una cadena con
probabilidades de transición estacionarías es v, entonces las probabilidades de los
diversos estados en el instante de tiempo n + 1 se especifican por el vector de
probabilidades vPn.
Ejemplo 3: Probabilidades para el número de líneas telefónicas ocupadas.
Considérese de nuevo la oficina con cinco líneas telefónicas y la cadena de Markov
para la cual la matriz de transición P está dada por la ecuación (2). Supóngase que al
inicio del proceso de observación en el instante de tiempo n = 1 la probabilidad de
que no haya líneas ocupadas es 0.5, la probabilidad de que haya una línea ocupada
es 0.3 y la probabilidad de que haya dos líneas ocupadas es 0.2. Entonces el vector
de probabilidades iniciales es v = (0.5, 0.3, 0.2, 0,0,0). En primer lugar, se
determinará la probabilidad de que exactamente j líneas estén ocupadas en el
instante de tiempo 2, un instante después. Por medio de cálculos elementales resulta
que
Puesto que la primera componente de este vector de probabilidades es 0.13, la
probabilidad de que no haya líneas ocupadas en el instante de tiempo 2 es 0.13;
puesto que la segunda componente es 0.33, la probabilidad de que exactamente una
línea esté ocupada en el instante de tiempo 2 es 0.33 y así sucesivamente.
Se determinará a continuación, la probabilidad de que haya exactamente j líneas
ocupadas en el instante de tiempo 3.
Utilizando la ecuación (3), se deduce
Puesto que la primera componente de este vector de probabilidades es 0.133, la
probabilidad de que no haya líneas ocupadas en el instante de tiempo 3 es 0.133;
puesto que la segunda componente es 0.227, la probabilidad de que exactamente
una línea esté ocupada en el instante de tiempo 3 es 0.227, y así sucesivamente.
Probabilidad y Estadística
Probabilidad condicional - CADENAS DE MARKOV
EJERCICIOS
1. Supóngase que el clima sólo puede ser soleado o nublado y que las
condiciones del clima en mañanas sucesivas forman una cadena de Markov con
probabilidades de transición estacionarias. Supóngase también que la matriz
de transición es la siguiente:
(a) Si un día concreto está nublado, ¿cuál es la probabilidad de que también
esté nublado el día siguiente?
(b) Si un día concreto hace sol, ¿cuál es la probabilidad de que durante los dos
días siguientes continúe haciendo sol?
(c) Si un día concreto está nublado, ¿cuál es la probabilidad de que al menos
uno de los tres días siguientes haga sol?
2. Considérese de nuevo la cadena de Markov descrita en el ejercicio 1.
(a) Si un miércoles hace sol, ¿cuál es la probabilidad de que el sábado
siguiente haga sol?
(b) Si un miércoles está nublado, ¿cuál es la probabilidad de que el sábado
siguiente haga sol?
3. Considérense de nuevo las hipótesis de los ejercicios 1 y 2.
(a) Si un miércoles hace sol, ¿cuál es la probabilidad de que el sábado y
domingo siguientes haga sol?
(b) Si un miércoles está nublado, ¿cuál es la probabilidad de que el sábado y
el domingo siguientes haga sol?
4. Considérese de nuevo la cadena de Markov descrita en el ejercicio 1.
Supóngase que la probabilidad de que un miércoles haga sol es 0.2 y que la
probabilidad de que esté nublado es 0.8.
(a) Determínese la probabilidad de que esté nublado el jueves siguiente.
(b) Determínese la probabilidad de que esté nublado el viernes.
(c) Determínese la probabilidad de que esté nublado el sábado.
Probabilidad y Estadística
Probabilidad condicional - CADENAS DE MARKOV
5. Supóngase que un estudiante llegará a tiempo o tarde a una clase y que los
sucesos de que llegue a tiempo o tarde a clase en días sucesivos forman una
cadena de Markov con probabilidades de transición estacionarias. Supóngase
también que si llega tarde un día, entonces la probabilidad de que llegue a tiempo
el día siguiente es 0.8. Además, si llega a tiempo un día, entonces la probabilidad
de que llegue tarde al día siguiente es 0.5.
(a) Si el estudiante llega tarde un día, ¿cuál es la probabilidad de que llegue
a tiempo los tres días siguientes?
(b) Si el estudiante llega a tiempo un día, ¿cuál es la probabilidad de que
llegue tarde los tres días siguientes?
6. Considérese de nuevo la cadena de Markov descrita en el ejercicio 5.
(a) Si el estudiante llega tarde el primer día de clase, ¿cuál es la probabilidad de
que llegue a tiempo el cuarto día?
(b) Si el estudiante llega a tiempo el primer día de clase, ¿cuál es la
probabilidad de que llegue a tiempo el cuarto día?
7. Considérense de nuevo las hipótesis de los ejercicios 5 y 6. Supóngase que la
probabilidad de que el estudiante llegue tarde en el primer día de clase es 0.7 y
que la probabilidad de que llegue a tiempo es 0.3
(a) Determínese la probabilidad de que llegue tarde el segundo día de clase.
(b) Determínese la probabilidad de que llegue a tiempo el cuarto día de clase.
8. Supóngase que una cadena de Markov tiene cuatro estados s1, s2, s3, s4 y probabilidades de transición estacionarías como se especifica en la matriz de
transición siguiente:
(a) Si la cadena está en el estado s3 en un instante de tiempo n, ¿cuál es la
probabilidad de que esté en el estado s¡ en el instante de tiempo n + 2?
(b) S¡ la cadena está en el estado «j en un instante de tiempo n, ¿cuál es la probabilidad de que esté en el estado 53 en el instante de tiempo n + 3?
9. Sea X1 el estado inicial en el instante de tiempo 1 de la cadena de Markov con la
matriz de transición especificada en el ejercicio 8 y supóngase que las
probabilidades iniciales son las siguientes:
Determínense las probabilidades de que la cadena esté en los estados s1, s2, s3, y
Probabilidad y Estadística
Probabilidad condicional - CADENAS DE MARKOV
s4 en el instante de tiempo n para cada uno de los siguientes valores de n: (a)
n = 2; (b) n = 3; (c) n = 4.
10. Cada vez que un cliente compra un tubo de pasta de dientes, elige la marca
A o la marca B. Supóngase que la probabilidad de que elija la misma marca
que en la compra anterior es 1/3 y que la probabilidad de que cambie de
marca es 2/3.
(a) Si la primera compra es de la marca A, ¿cuál es la probabilidad de que la
quinta compra sea de la marca B?
(b) Si la primera compra es de la marca B, ¿cuál es la probabilidad de que la
quinta compra sea de la marca B?
11. Supóngase que tres niños A, B y C se pasan una pelota uno a otro. Cuando A
tiene la pelota se la pasa a B con probabilidad 0.2 y a C con probabilidad
0.8. Cuando B tiene la pelota se la pasa a A con probabilidad 0.6 y a C con
probabilidad 0.4.
Cuando C tiene la pelota es igualmente probable que se la pase a A que a B.
(a) Considérese este proceso como una cadena de Markov y calcúlese la matriz
de transición.
(b) Si es igualmente verosímil que cada uno de los tres niños tenga la pelota
en un tiempo n concreto, ¿qué niño tendrá la pelota con mayor
probabilidad en el instante de tiempo n + 2?
12. Supóngase que se lanza repetidamente una moneda de forma que en un
lanzamiento es igualmente probable que aparezca una cara que una cruz y que
los lanzamientos son independientes, con la siguiente excepción: Cuando se
han obtenido tres caras o tres cruces en tres lanzamientos sucesivos, entonces
el resultado del siguiente lanzamiento es siempre del otro tipo. En el
tiempo n (n ≥ 3), el estado de este proceso es el especificado por los
resultados de los lanzamientos n — 2, n - 1 y n. Demuéstrese que este
proceso es una cadena de Markov con probabilidades de transición
estacionarias y calcúlese la matriz de transición.
13. Existen dos urnas A y B, conteniendo cada una bolas rojas y verdes.
Supóngase que la urna A contiene una bola roja y dos verdes y que la urna B
contiene ocho bolas rojas y dos verdes. Considérese el siguiente proceso: Se
extrae aleatoriamente una bola de la urna A y se extrae aleatoriamente una
bola de la urna B. La bola extraída de la urna A se introduce en la urna B y
la bola extraída de la urna B se introduce en la urna A. Estas operaciones se
repiten indefinidamente. Demuéstrese que los números de bolas rojas en la urna
A constituyen una cadena de Markov con probabilidades de transición
estacionarias y calcúlese la matriz de transición de la cadena de Markov.
Probabilidad y Estadística