Guía 1: Fracciones decimales - Colegio de los Sagrados Corazones
Anuncio
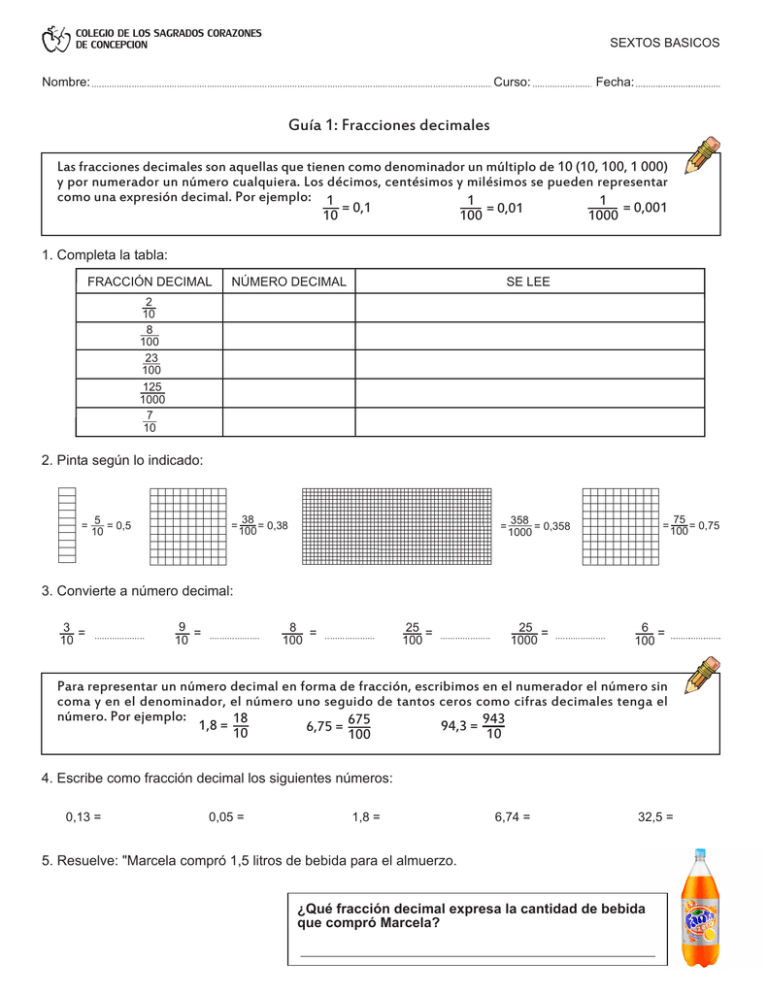
COLEGIO DE LOS SAGRADOS CORAZONES DE CONCEPCION SEXTOS BASICOS Curso: Nombre: Fecha: Guía 1: Fracciones decimales Las fracciones decimales son aquellas que tienen como denominador un múltiplo de 10 (10, 100, 1 000) y por numerador un número cualquiera. Los décimos, centésimos y milésimos se pueden representar como una expresión decimal. Por ejemplo: 1 1 = 0,01 1 = 0,001 = 0,1 100 10 1000 1. Completa la tabla: FRACCIÓN DECIMAL NÚMERO DECIMAL SE LEE 2 10 8 100 23 100 125 1000 7 10 2. Pinta según lo indicado: = 5 = 0,5 10 = 38 = 0,38 100 = 358 = 0,358 1000 = 75 = 0,75 100 3. Convierte a número decimal: 3 = 10 9 = 10 8 = 100 25 = 100 25 = 1000 6 = 100 Para representar un número decimal en forma de fracción, escribimos en el numerador el número sin coma y en el denominador, el número uno seguido de tantos ceros como cifras decimales tenga el número. Por ejemplo: 1,8 = 18 94,3 = 943 6,75 = 675 10 10 100 4. Escribe como fracción decimal los siguientes números: 0,13 = 0,05 = 1,8 = 6,74 = 32,5 = 5. Resuelve: "Marcela compró 1,5 litros de bebida para el almuerzo. ¿Qué fracción decimal expresa la cantidad de bebida que compró Marcela? COLEGIO DE LOS SAGRADOS CORAZONES DE CONCEPCION SEXTOS BASICOS Curso: Nombre: Fecha: Guía 2: Valor posicional en los números decimales Para leer y escribir números decimales: 1° Se comienza por la parte entera seguida de la palabra "enteros". 2° Luego, se lee y escribe la parte decimal seguida de la palabra "décimos", "centésimos" o "milésimos". 1. Escribe el nombre de los números decimales: 0,7 = 25,8 = 1,8 = 1,05 = 4,32 = 4,003 = 2. Escribe los numeros decimales correspondientes: Ocho enteros y sesenta y siete centésimos Ciento cuarenta y cinco milésimos Dos enteros y veinticnco milésimos Un entero y ocho centésimos Treinta enteros y cuatro centésimos Ocho enteros y nueve décimos En el sistema de numeración decimal, el valor de una cifra depende de la posición que ocupa. En el caso de los números decimales, además de la parte entera, existe una parte decimal y los ubicados en ella tendrán distinto valor dependiendo del lugar que ocupen. PARTE ENTERA PARTE DECIMAL DECENA 4 UNIDAD 3 , , DÉCIMO 0 CENTÉSIMO 5 MILÉSIMO 6 3. ¿Cuál es la posición del dígito en negrita? 6,59 12,41 23,007 42,54 4. ¿Cuál es el valor del dígito subrayado? 0,125 125,5 34,07 0,893 5. Escribe los números en forma desarrollada. Por ejemplo: 5,643 = 5 + 0,6 + 0,04 + 0,003 12,6 0,428 8,256 63,45 6. Resuelve: "La altura de tres hermanos es la siguiente: Andrea: 1,70 m., Alejandra: 1,68 m. y Joaquín: 1,75 m. ¿Cuál hermano tiene mayor estatura? COLEGIO DE LOS SAGRADOS CORAZONES DE CONCEPCION SEXTOS BASICOS Curso: Nombre: Fecha: Guía 3: Orden y comparación de números decimales Para comparar números decimales se empieza por comparar las cifras con mayor valor posicional. Cuando es necesario, se iguala la cantidad de cifras decimales agregando ceros. Por ejemplo: 1,8 y 1,82 queda 1,80 y 1,82 Enteros iguales Décimos iguales Centésimos distintos: 1=1 0,8 = 0,8 0<2 por lo tanto, 1,8 < 1,82 1. Escribe “mayor que” >, “menor que” < o “igual a” = entre los decimales: 0,564 0,645 12,8 1,288 6,582 6,676 4,12 4,012 1,56 1,560 34,3 34,24 0,607 0,67 2,00 0,2 2. Ordena los números decimales de menor a mayor: 2,76 - 2,803 - 2,098 - 12,8 - 2,009 < < < < 3. Completa el recuadro con el número decimal que corresponde: 0,04 < < 0,05 1,24 < < 1,25 0,36 < < 0,365 4. Ordena los números decimales en forma descendente: 8,67 - 0,867 - 86,67 - 8,067 - 8,607 > > > > 5. Pinta todas las etiquetas que sean menores que 0,5 0,45 0,6 0,367 0,1 2 1,1 0 ,0 9 6. Ordena los animales del más fuerte al menos fuerte. Numera: Tigre. Pueden arrastrar hasta 2,5 veces su propio peso. Escarabajo rinoceronte. Pueden levantar 850 veces su propio peso. Oso. Pueden levantar 0.8 veces su propio peso. Elefante. Pueden transportar hasta 1,3 veces su propio peso. 7. Resuelve: "Gloria se tomó la temperatura. El térmometro marcó un número entre 37,5 °C y 37,7 °C" ¿Cuántos grados habrá marcado el termómetro? COLEGIO DE LOS SAGRADOS CORAZONES DE CONCEPCION SEXTOS BASICOS Curso: Nombre: Fecha: Guía 4: Equivalencia entre fracciones y números decimales Para expresar una fracción como número decimal se pueden usar varias estrategias, por ejemplo, dividir el numerador por el denominador. 1 10 : 2 = 0,5 1 = 0,5 2 - 10 2 0 1. Escribe el número decimal que corresponde a cada fracción: 1 = 4 2 = 4 3 = 4 4 = 4 1 14 = 2. Completa con la fracción y el número decimal que corresponda a cada representación: = = = = = = = = = = = = Para expresar un número decimal como fracción se transforma el número a fracción decimal y luego se simplifica para obtener una fracción irreductible. Por ejemplo: 8 :2 = 4 0,8 = 8 10 10 : 2 5 3. Expresa cada número decimal como fracción irreductible: 0,4 = 0,7 = 0,25 = 0,625 = 1,5 = 3,75 = 0,125 = 0,6 = 4. Resuelve: "A qué número decimal representa la parte pintada de la figura?" La parte pintada corresponde al decimal: COLEGIO DE LOS SAGRADOS CORAZONES DE CONCEPCION SEXTOS BASICOS Curso: Nombre: Fecha: Guía 5: Números decimales en la recta numérica Para ubicar un número decimal en la recta numérica, se divide la unidad en diez partes iguales, así se detrminan las décimas. Las centésimas, a su vez se determinan dividiendo cada décima en diez partes iguales. 0,2 0 0,4 0,6 0,8 1 1. Escribe los números decimales correspondientes a cada letra: A 0 B A = B = E 4 C 1 C = F E = I K 3,7 J = I = M 12,5 12,51 M = H = 3,8 12,52 L = 12,53 N = L 3,9 K = N H 6 G = J 3,6 D = G 5 F = 3,5 D 2 Ñ 12,54 O O = Ñ = 2. Ubica las fracciones, números mixtos y números decimales en la recta numérica: 1 2 0 0,25 0,8 10 10 1,9 1 12 1,3 3. Resuelve: "¿Qué número decimal se podría ubicar entre 1/4 y 1/2? Se podría ubicar el decimal: 0 1 4 1 2 1 2 2,5 COLEGIO DE LOS SAGRADOS CORAZONES DE CONCEPCION SEXTOS BASICOS Curso: Nombre: Fecha: Guía 6: Aproximación de números decimales En la aproximación por redondeo de números decimales, si la cifra que sigue a la que se quiere aproximar es menor que 5, esta última se deja igual y si la cifra que sigue a la que se quiere aproximar es igual o mayor que 5, esta última se aproxima a la unidad siguiente. Por ejemplo: NÚMERO 2,3 12,64 3,06 234,122 45,679 A LA UNIDAD A LA DÉCIMA 2 13 3 234 46 A LA CENTÉSIMA 12,6 3,1 234,1 45,7 234,12 45,68 1. Aproxima los siguientes números por redondeo a la centésima: 14,259 = 22,157 = 332,416 = 8,609 = 78,998 = 50,009 = 334,895 = 6,556 = 45,803 = Otra forma de aproximación es por truncamiento, y consiste en suprimir las cifras a partir del orden de aproximación. Por ejemplo: 34,7 truncado al entero es 34 9,72 truncado a la décima es 9,7 83,289 truncado a la centésima es 83,28 2. Completa la tabla: Números decimales Aproximación por redondeo Al entero A la décima A la centésima Aproximación por truncamiento Al entero A la décima A la centésima 5,475 26,136 844,123 7,058 3. Resuelve: "Si el promedio de Pamela en Matemática es 5,58. ¿Qué sería más conveniente para Pamela, que el profesor aproximara por redondeo o por truncamiento?, ¿por qué?" Lo más conveniente sería: COLEGIO DE LOS SAGRADOS CORAZONES DE CONCEPCION SEXTOS BASICOS Curso: Nombre: Fecha: Guía 7: Adición y sustracción de números decimales Para resolver adiciones o sustracciones de números decimales se ordenan de manera vertical, alineados por la coma decimal. Si la cantidad de cifras decimales no es igual, se completa con ceros y se realiza el cálculo. Por ejemplo: 23,60 23,6 + 0,26 + 0,26 23,86 1. Resuelve las adiciones, en forma vertical: 0,5 + 0,24 = 12,02 + 6,76 = 0,765 + 2,9 = 8,68 + 6,82 = 4,123 - 3,91 = 12,4 - 0,883 = 2. Resuelve las sustracciones, en forma vertical: 2,6 - 1,3 = 8,56 - 3,05 = 3. Desarrolla los siguientes problemas: a) Un canasto vacío pesa 0,5 kg y lleno con manzanas 1,75 kg. ¿Cuánto pesan las manzanas? b) Un ciclista recorrió 12,7 km en la primera etapa; 10,25 km. en la segunda etapa y 11,05 en la etapa final. ¿Cuántos kilómetros recorrió en total? c) Se reunen tres bebidas: Bilz: 1,5 litros; Pap: 2,5 litros y Kem: 1,25 litros. ¿Cuántos litros faltan si se quieren reunir 6 litros? d) Ayer, la temperatura mínima observada fue de 8,6 °C y la temperatura máxima se registró a las 12:00 hrs y fue de 19,8 °C. ¿Cuántos grados hay de diferencia entre las dos temperaturas? e) Carolina se subió a la balanza y registró 45,8 kg. luego volvió a subirse con su gato y ahora la balanza registró 48,35 kg. ¿Cuál es el "peso" del gato? 4. Resuelve: "La cancha de fútbol tiene 12,5 metros de largo y 0,85 metros de ancho" ¿Cuál es su perímetro?





