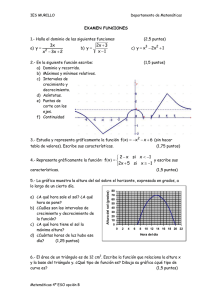
Funciones Especiales

FUNCIONES ESPECIALES
Tipo de
Función
Funciones
definidas a
Trozos
o
por intervalos
Función
valor
absoluto
Expresión algebraica y
Clase de gráfica
Características y
Observaciones
 f1 ( x) para Dom f1

y =  f 2 ( x) para Dom f 2
   

La unión de los intervalos
que determinan los
tramos conforma el
dominio de la función
Su gráfica se compone de
“varios trozos” cada uno
correspondiente al
intervalo representado
Los “tramos” se enumeran en orden, de
izquierda a derecha, indicando en cada
uno la expresión que define la función
en ese intervalo.
− x si x < 0
y x= 
=
 x si x ≥ 0
Dom f = 
Esta función asocia a cada número su
valor absoluto, es decir su valor
prescindiendo del signo
La forma de su gráfica se
parece a una V
mayúsculas (con
expresiones lineales)
Función
Parte
Entera
y = [ x]
2
− x − 2 x − 3 si x ≤ 0
y=
si x > 0
 x + 1
si x ≤ −2
1

y  x2
si − 2 < x ≤ 1
=
 x − 3 si x > 1


y= x − 5
⇓
− ( x − 5 ) si x < 5
y=
si x ≥ 5
x − 5
Se pueden transformar en funciones a
trozos de esta forma:
· Igualamos a cero para hallar sus raíces
· Se forman intervalos con las raíces y se
evalúa el signo de cada intervalo
· Definimos los tramos considerando que
los intervalos donde “x” es negativo se
cambia el signo de la función
Traslaciones de la gráfica:

k <0
→
y = x + k ⇒ ←
k >0
y= x + k ⇒ k > 0↑↓ k < 0
Mayor número entero inferior o igual a x
Asigna a cada número real el menor de
los enteros entre los que está
comprendido
f ( x) = E ( x)
Dom f = 
f : → 
[ x] ≤ x < x + 1
Su gráfica es una sucesión
de segmentos
horizontales a distintas
alturas.
También llamada función escalonada
No es continua en los números enteros
pero si en los tramos, donde es
constante y vale n.
Ejemplos :
Función
Parte
decimal
ó
Función
Mantisa
Función
Signo
y= x − [ x ]
Su gráfica es una sucesión de segmentos
inclinados de pendiente 1
f ( x)= x − E ( x)
Dom f = 
Es una función periódica de periodo 1
y = sgn( x)
Se define como una función dada por
intervalos del siguiente modo
Dom f = 
Im f =
Algunos
Ejemplos
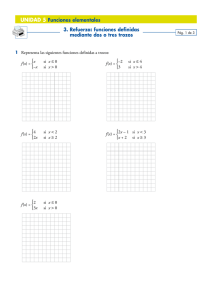
Estas funciones requieren varias
fórmulas, cada una de las cuales rige el
comportamiento de la función en un
cierto tramo o "trozo".
Para representar estas funciones
representamos cada uno de los trozos y
nos fijamos en el comportamiento de la
función en los puntos de ruptura (puntos
en los que se pasa de un trozo a otro).
Im f =  +
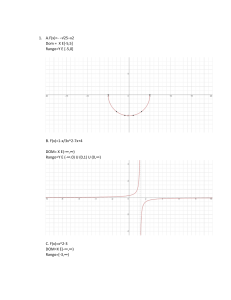
Representación gráfica y
Tabla de valores
{−1, 0,1}
[ π]= 3 → 3 ≤ π < 4
[ −π] = −4 → − 4 ≤ −π < −3
La descomposición en parte entera y
decimal es obvia en los números
positivos: 1,732 = 1 + 0.732,
pero no tanto en los negativos:
- 2.23606 = - 3 + 0.76394.
−1 si x < 0

0 si x 0
=
f ( x) =
 1 si x > 0

Math Quick Reference Card ─ TIPOS DE FUNCIONES 1.2 ─ (cc) www.3con14.com