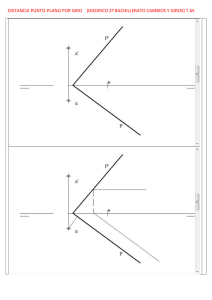
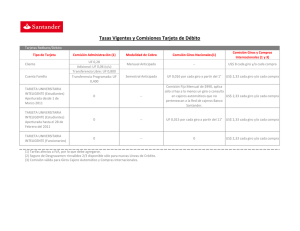
Uniones flexibles
Anuncio

Uniones flexibles entre los elementos estructurales J. T. Celigüeta Uniones flexibles Q Q Q Q Unión entre dos piezas, o entre una pieza y el suelo, no ideal: X Permite el movimiento relativo entre ambas piezas X Deformaciones diferentes en ambas piezas unidas Debida a la deformación de los elementos de unión entre las piezas (tornillos, chapas…) La unión flexible produce unas fuerzas / momentos proporcionales a la diferencia de deformaciones Efecto avanzado, que sólo se tiene en cuenta en algunos casos. 1 Uniones flexibles al giro Q Q Q Q Unión al giro entre dos piezas no ideal : X ni totalmente articulada ni totalmente empotrada Debida a la deformación de los elementos de unión entre las piezas Permite el giro relativo entre ambas piezas: giros diferentes en ambas piezas unidas La unión flexible produce un momento proporcional a la diferencia de giros 1 2 2 Modelización de uniones flexibles al giro Q Q Se modelizan como un resorte al giro que conecta las dos piezas unidas, y que produce un momento proporcional al giro relativo X Dificultad: estimar la rigidez de la unión Se transmiten perfectamente N, y Q: unión perfecta en los desplazamientos. 1 2 3 Rigidez de las uniones flexibles al giro M 1 = K (θ1 − θ2 ) M 2 = K (θ2 − θ1 ) = −M 1 ⎧ M ⎫ ⎧K ⎪ ⎪ 1 ⎪⎪ = ⎪ ⎪ ⎨ ⎬ ⎨ ⎪ ⎪M 2 ⎪⎭⎪ ⎪− ⎪ K ⎩ ⎩ θ⎫ −K ⎫⎧ ⎪⎪ ⎪⎪ 1 ⎪ ⎪ ⎬⎨ ⎬ K ⎪⎪ ⎪⎪θ2 ⎪⎭ ⎪ ⎭⎩ El muelle acopla los dos giros, pero no afecta a las fuerzas 4 Pretensión inicial en muelles al giro Se puede considerar, como en cualquier muelle. Corresponde a un momento de montaje del muelle M0, asociado a una diferencia en el giro entre sus extremos θ0 Efecto más teórico que real, por la dificultad de materializarlo. Q Q Q Se conoce directamente el momento de pretensión Fase 0 M ⎧⎪−M 0 ⎫ ⎪ ⎪ ⎪ =⎨ ⎬ ⎪+ M ⎪ 0⎪ ⎪⎩ ⎭ Fase 0 M M0 5 Se conoce el error angular entre sus extremos M0 ⎡K = − ⎢⎢ ⎢⎣−K 0 −K ⎤ ⎪⎧ 0 ⎪⎫ ⎪⎧+K θ0 ⎪⎫ ⎪ ⎥ ⎨⎪ ⎬⎪ = ⎨⎪ ⎬ +K ⎥⎥ ⎪⎪θ0 ⎪⎪ ⎪− K θ0 ⎪⎪ ⎪ ⎦⎩ ⎭ ⎩ ⎭ Ejemplo q Y X A 1 2 B H ⎧ EA 12EI ⎪ ⎪ + ⎪ H3 ⎪⎪ L ⎪⎪ 0 ⎪⎪ ⎪ ⎨ ⎪ ⎪ 0 ⎪ ⎪ ⎪⎪ ⎪ 6EI ⎪ ⎪ ⎪ H2 ⎪ ⎩ 0 0 EA 12EI + L3 H 6EI − 2 L 6EI L2 4EI +K L 0 −K − ⎫ ⎪ ⎪ ⎪ ⎪⎪ ⎧Δ ⎫ ⎧ F ⎫ ⎪⎪ ⎪⎪ X ⎪⎪ ⎪⎪ X ⎪⎪ ⎪ ⎪ ⎪ ⎪ 0 ⎪⎪ ⎪⎪ΔY ⎪⎪ ⎪⎪ FY ⎪⎪ ⎪ ⎪ ⎪ ⎬⎨ ⎬ = ⎪ ⎨ ⎬⎪ ⎪⎪ θ1 ⎪⎪ ⎪⎪M 1 ⎪⎪ ⎪⎪ −K ⎪⎪ ⎪ ⎪⎪ ⎪⎪ ⎪⎪ ⎪ ⎪⎪ θ2 ⎪⎪ ⎪⎪M 2 ⎪⎪ ⎪⎪ ⎩ ⎭ ⎩ ⎭ ⎪ 4EI ⎪ + K⎪ H ⎪ ⎭⎪ 6EI H2 L Fuerzas equivalentes a la carga distribuida 6 0 ⎧⎪ ⎫⎪ ⎪⎪ ⎪⎪ ⎧⎪ FX ⎫⎪ ⎪ ⎪⎪ ⎪⎪ ⎪ ⎛⎜qL ⎞⎟ ⎪⎪ ⎪⎪ FY ⎪⎪ ⎪⎪ − ⎜⎝ 2 ⎠⎟⎟ ⎪⎪ ⎪⎨ ⎪⎬ = ⎪⎨⎪ ⎪⎬⎪ ⎪⎪M 1 ⎪⎪ ⎪⎪ ⎛⎜ qL2 ⎞⎟⎪⎪ ⎟⎟⎪ ⎪⎪ ⎪⎪ ⎪⎪− ⎜⎜− ⎪⎪ 12 ⎝ ⎠ M ⎪⎪ 2 ⎪⎪ ⎪⎪ ⎪⎪ ⎩ ⎭ ⎪ 0 ⎪ ⎪ ⎪ ⎪ ⎩ ⎭ El muelle acopla los dos giros Resultados numéricos L=H=500 cm IPE 200 A:28 cm2 I=1940 cm4 0 0 ⎧⎪119700 + 391 ⎪ ⎪ 0 391 + 119700 −97776 ⎪⎪ ⎪ ⎨ 7 7 0 97776 3 1 0 4 10 − ⋅ + ⋅ ⎪ ⎪ ⎪ ⎪⎪ 97776 0 −4 ⋅ 107 ⎪⎩ ⎪ ⎧⎪ΔX ⎫⎪ ⎧− 0.07346⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ 0.0699 − Δ ⎪ ⎪ ⎪ Y⎪ ⎪=⎪ ⎪ ⎨ ⎬ ⎨ ⎬⎪ 0.016357 ⎪ ⎪ ⎪ θ1 ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ 0.009023 θ2 ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎭ ⎩ ⎭ ⎩ M 2 = K (θ2 − θ1 ) = −293370 cmkg M 1 = −M 2 = 293370 7 q=40 kg/cm K=4 107 cm kg ⎫⎪ ⎧ ΔX ⎫ 0 ⎫ ⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ 0 ⎪ ⎪ΔY ⎪ ⎪⎪ −1000 ⎪⎪ ⎪ ⎪ ⎪⎬ = ⎨⎪ ⎬⎨ ⎬⎪ 7 −4 ⋅ 10 ⎪⎪ θ1 ⎪⎪ ⎪⎪833333⎪⎪ ⎪⎪ ⎪⎪ ⎪⎪ ⎪⎪ ⎪⎪ 7 7 ⎪⎪ 0 θ ⎪⎪ ⎪ ⎪ ⎪ 3 ⋅ 10 + 4 ⋅ 10 ⎪⎪⎩ 2 ⎪⎭ ⎪⎩ ⎪⎭ ⎪ ⎭ 97776 Otras uniones flexibles Q Q Q Flexibilidad axial y/o cortante Menos habituales que las uniones flexibles al giro Se modelizan como un resorte que conecta las dos piezas unidas, y que produce una fuerza proporcional al desplazamiento relativo X Dificultad: estimar la rigidez de la unión Y2 X1 8 Y1 X2 Modelización en la práctica Q Q Q Hay varias deformaciones en un mismo nudo. Programas que permiten varias deformaciones en un mismo nudo. Muy poco habituales. X Varios giros en un mismo nudo. Algunos pocos programas lo permiten (cespla) Programas donde el número de deformaciones en cada nudo es fijo (3 en el plano, 6 en el espacio). Lo más habitual en la práctica. X Se deben crear dos nudos, muy cercanos entre si. X Unir los dos nudos mediante resortes en las tres / seis direcciones: se debe introducir la flexibilidad en todas las direcciones. 9