Capítulo 6. Sistemas Reales

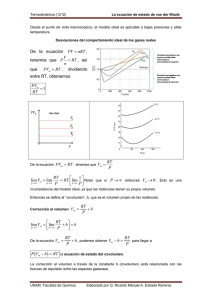
CAPITULO 6
SISTEMAS REALES
Recopilación de Mauricio Pilleux
6.1 DESVIACIONES DE LA LEY DE GAS IDEAL
(http://waugh.cchem.berkeley.edu/web/deviations_from_ideal.html)
6.1.1 Desviaciones de la Ley de Gas Ideal
La ley del gas ideal no siempre predice con precisión el comportamiento de
todos los gases. Por ejemplo, a medida que se enfría el vapor, éste comienza a
condensar en agua. Sería útil tener una ley de gases que considere el proceso
de la condensación del vapor, al igual que otros comportamientos
experimentales que no son considerados por el modelo ideal.
La ley de gas ideal es muy buena en algunos dominios de temperatura y
presión, pero los gases se comportan de otra forma cuando las temperaturas
bajan o cuando la presión aumenta. Esto se debe a que las suposiciones
usadas en la ley de gas ideal dejan de ser válidas y, por lo tanto, se deben
deducir leyes más precisas en un rango de dominios más amplio.
6.1.2 Suposiciones de la Ley de Gas Ideal
La ley de gas ideal supone lo siguiente:
•
•
•
Las moléculas de gas son partículas puntuales. Las partículas
puntuales no ocupan volumen en el espacio; sólo son un punto
unidimensional.
Las moléculas sufren colisiones elásticas. Las colisiones elásticas
conservan la energía cinética, por lo tanto, cuando la partícula choca con
la pared o con otra partícula, la energía no se convierte en energía
potencial o calor.
El único tipo de interacciones son las colisiones. Esto se debe a que
las colisiones son elásticas. Para que exista una interacción de atracción
o repulsión tendría que existir un término de energía potencial. Como en
una colisión elástica no puede haber una transferencia de energía hacia o
desde una energía potencial, no existen interacciones entre las partículas
o entre las partículas y las paredes del recipiente.
6.1.3 Consecuencias de las Suposiciones Ideales
Este conjunto de suposiciones predice que es posible comprimir indefinidamente
una muestra de gas. Como las moléculas de gas no ocupan un volumen físico,
es posible comprimirlas infinitamente cercanas entre sí. Las moléculas nunca se
________________________________________________________________________________________________
Capítulo 6. Sistemas Reales
1
repelerán entre sí ya que no existen interacciones entre moléculas. El problema
es que las moléculas reales ocupan un espacio físico no nulo. Por lo tanto, la
ley de gas ideal tiene una falla fundamental.
Una segunda consecuencia de la no existencia de interacciones en el gas es
que este siempre permanecerá en dicho estado y no ocurrirá la condensación.
Esto se debe a que la condensación requiere de una fuerza atractiva entre
partículas, de manera que éstas se puedan aglomerar cuando el término de
energía cinética es sobrepasado por el de energía potencial atractiva entre
partículas. La condensación es un hecho experimental, de manera que debe
existir un término de atracción entre las moléculas de gas.
6.1.4 ¿Hasta Cuándo es Válida la Ley de Gas Ideal?
La ley de gas ideal es una buena aproximación cuando las suposiciones que se
hacen son esencialmente verdaderas. La suposición de partícula puntual se
cumple cuando el volumen ocupado por las moléculas es una proporción muy
pequeña del volumen total del recipiente ocupado por el gas y, por lo tanto, el
volumen de las moléculas puede despreciarse. Las suposiciones que las
colisiones son elásticas y que no hay interacciones son válidas cuando las
moléculas tienen tanta energía cinética que puede despreciarse el término de
energía potencial.
Por lo tanto, la ley de has ideal es válida sólo a bajas densidades y altas
temperaturas.
6.1.5 Ajustes a la Ley de Gas Ideal
El primer ajuste a la ley de gas ideal es la incorporación de un término que
considere el volumen molecular. Esto nos lleva al modelo de esferas duras.
Luego, el siguiente paso es incluir en este modelo de esferas duras un término
de atracción que permita la condensación. Esto da origen al modelo de van der
Waals, la cual será tratada más adelante en este capítulo.
Un gas ideal está caracterizado por dos ecuaciones
y
donde c es una constante y R es la constante universal de los gases (R = NAkB =
8,3144 J mol-1K-1). Los gases sin interacciones obedecen a este comportamiento
a temperaturas tales que kBT es pequeño comparado con las energías de
excitación electrónica y las presiones son bajas. La ley de gas ideal es válida en
el régimen de densidades muy bajas – donde las interacciones entre moléculas
________________________________________________________________________________________________
Capítulo 6. Sistemas Reales
2
son esencialmente nula. Cuando la densidad aumenta, la ley de gas ideal
comienza a fallar.
Un primer intento de corregir la ley de gas ideal a mayores densidades se hace
mediante la incorporación de una interacción repulsiva intermolecular a corta
distancia. Esto lleva al modelo de “esferas duras” dado por la siguiente
ecuación:
donde el parámetro b representa la interacción repulsiva entre las moléculas y
normalmente se llama el "volumen excluido". Esta ecuación también se conoce
como ecuación de estado de Clausius. Los valores de b dependen del radio
molecular y un cálculo sencillo se puede realizar suponiendo interacciones entre
esferas duras (que no se deforman). El volumen excluido por las esferas duras
(moléculas gaseosas) es:
(se incluye el término 1/2 pues se requiere el volumen excluido por átomo y no
por par de átomos) lo cual se puede reducir a
Esta relación se conoce como el modelo gaseoso de las esferas duras. Hay que
notar que un gas de esferas duras ocupa un volumen dado y, por lo tanto, no
puede ser comprimido indefinidamente.
6.2 GASES REALES
6.2.1 Ecuación de Estado
(http://www-unix.ecs.umass.edu/~wconner/che226/Lect_13/Lect_13a.html)
Para poder trabajar, en todos los gases es necesario obtener una relación que
ligue las variables de estado P, V, T. Esto es la ecuación de estado:
f1(P,V,T) = 0
Como el volumen molar es v=V/n, luego
f2(P,v,T) = 0
________________________________________________________________________________________________
Capítulo 6. Sistemas Reales
3
o equivalentemente
v = v (P,T)
o una forma muy común de la ecuación de estado:
Pv = f(P,T)
6.2.2 Experimentos de Amagat
(http://www.physics.carleton.ca/~hardy/75342/Lect_6/Lect_6.html)
Una propiedad básica de cualquier gas es que su ecuación de estado se
aproxima a la de un gas ideal a medida que se permite que su presión disminuya
a cualquier temperatura sobre la temperatura crítica. Lo que sucede físicamente
es que la densidad baja, de manera que aumenta la distancia entre las
moléculas gaseosas y gradualmente se eliminan las fuerzas entre ellas, excepto
aquellas que surgen momentáneamente durante las colisiones, las cuales
también son menos esporádicas. El resultado tiene invariablemente la forma
lím( Pv ) = A(T )
P →0
Lo que indica que el producto Pv no depende de la naturaleza del gas. Por esta
razón A(T) es una buena magnitud termométrica y se establece por definición
que
A = Rθ
donde θ es la temperatura en la escala de gases ideales. Además, se establece
que
θ(punto triple del agua) ≡ θt ≡ 273,16 K
entonces
lím( Pv ) t = R × 273,16 K
P →0
por lo tanto
R=
1
lím( Pv ) t
273,16 K P→0
(El subíndice t denota que se trata de un gas real en equilibrio térmico con el
sistema t.)
El valor medido y aceptado para de R es el siguiente:
R = 8,31451 ± 8,4 ppm J mol −1 K −1
6.2.3 Expansión Virial
La propiedad de todos los gases para cumplir que
lím( Pv ) = A(T )
P →0
________________________________________________________________________________________________
Capítulo 6. Sistemas Reales
4
se utiliza en la expansión virial, que es una aproximación de la ecuación de
estado del gas ideal:
o
donde A = RT es el primer coeficiente virial universal. B, C, D, etc., son los
llamados segundo, tercer, cuarto, etc., coeficientes del virial y aparecen
tabulados en muchos libros de gases comunes. Estos coeficientes son
específicos de cada gas, dependen de su temperatura y su valor decrece: B>>
C>>D>>… La razón por la cual estos coeficientes decrecen y se hacen
despreciables es que consideran las fuerzas asociadas con colisiones de
muchos cuerpos en un gas: B’, dos cuerpos; C’, tres cuerpos, D’, cuatro cuerpos,
etc. La palabra virial viene de la palabra latina (vis, vires) que significa fuerza.
A la expresión
Pv
RT
se le denomina factor de compresibilidad y, en un gas ideal, Z=1. Este factor
indica cuánto se aparta un gas del comportamiento ideal.
Z=
Los coeficientes del virial se pueden obtener de dos formas:
1. Mediante ajuste de curvas en experimentos isotermales, lo cual da los
mejores valores de ajuste para cada temperatura.
2. Calculándolos de modelos teóricos de las fuerzas intermoleculares. Esto se
hace más difícil a medida que aumenta el orden del coeficiente.
No es difícil observar por qué a una colisión de n cuerpos contribuye un término
~v-(n-1). Si r es la distancia máxima cercanía entre dos moléculas en un gas que
contiene N=nNA moléculas en un volumen V=nv. Como la distribución de
moléculas es aleatoria, la probabilidad que una molécula dada tenga a otra
molécula dentro de una distancia r es
Este número es siempre <<1 para los gases
,
pero es ~1 para los líquidos.
Ahora, en cualquier instante, si en el gas se eligen todos los pares de moléculas
________________________________________________________________________________________________
Capítulo 6. Sistemas Reales
5
que colisionan, la fracción de ellas que tienen una tercera molécula dentro de
una distancia r es
de manera que la probabilidad de la colisión de tres cuerpos es del orden de
Por lo tanto, se puede concluir que a la colisión de n cuerpos contribuye un
término ~v-(n-1).
Ejemplo: Un problema de temperatura empírica
Un termómetro de gas contiene n = 0,05 moles de gas en un volumen de
1,0 litro. El gas se supone ideal, pero en realidad obedece la siguiente
ecuación de estado de van der Waals:
donde P está en atmósferas y v=V/n está en litros.
¿Cuál es el error en la temperatura empírica registrada por el termómetro
a 100 ºC?
La temperatura empírica T(P) registrada en un gas ideal sería
precisamente 373,15 K, ya que la temperatura del gas ideal coinciden con
las temperatura absolutas. La temperatura empírica real es
donde
mientras que
.
En consecuencia, Θ(P)=373,33 K, de manera que el error es
Θ(P) - T =373,33 K– 373,15 K= 0,18 K a 100 ºC.
________________________________________________________________________________________________
Capítulo 6. Sistemas Reales
6
6.3 SISTEMA DE VAN DER WAALS
6.3.1 Introducción: Johannes Diderik van der Waals
(http://www.phys.tue.nl/vdwaals/alg/biovdwuk.htm)
Johannes Diderik van der Waals nació en Leiden, Holanda, el 23 de noviembre
de 1837 y sin duda es uno de los físicos holandeses más influyentes que haya
existido. En un principio, entre 1856 y 1861, van der Waals estudió para
converstirse en un profesor de escuela básica, pero luego continuó sus estudios
para director y asistió a cursos de matemáticas, física y astronomía en la
Universidad de Leiden. Desde 1866 enseñó física y matemáticas en escuelas
secundarias en La Haya y, en 1873, se graduó con su tesis: "Over de continuïteit
van de gas- en vloeistoftoestand" ("Sobre la continuidad de los estados gaseoso
y líquido"). En esta tesis publicó su conocida ley:
En 1877 J.D. van der Waals se convirtió en el primer profesor de física de la
Universidad Ilustre en Amsterdam. En 1880 formuló la “ley de los estados
correspondientes”, en 1893 una teoría de fenómenos capilares y en 1891 su
teoría del comportamiento de mezcla de dos materiales, lo cual no pudo ser
demostrado experimentalmente sino hasta 1941. En 1908, a la edad de 71 años,
van der Waals renunció como profesor. Falleció el 8 de marzo de 1923.
6.3.2 La ecuación de estado de van der Waals
La ecuación de estado más sencilla que predice la curva de inversión es la
ecuación de van der Waals. Esta ecuación entrega una curva de inversión que
está relativamente cerca de la real.
Antes de mostrar cómo funciona esta ecuación, resumamos las propiedades de
los gases reales:
1. Para valores grandes de PV, todos los gases tienden a ser ideales. Sus
isotermas se aproximan a una hipérbola equilátera en el plano P-V: PV=cte.
2. Todos los gases condensan a temperaturas bajas y a presiones altas. Cada
gas tiene su temperatura crítica, Tc, sobre la cual ninguna elevación de
presión puede hacer que se transforme en fase líquida. (Cuando su
temperatura está por debajo de su valor crítico, una sustancia en fase
gaseosa normalmente es llamada vapor.)
3. Cuando un vapor está en equilibrio con su fase condensada, su presión es
independiente de su volumen, con P = P(T) solamente.
4. Los vapores pueden ser “subenfriados” sin que condensen y las fases
líquidas pueden ser “sobrecalentadas” sin que ebullan. Estas dos fases son
metaestables y se pueden presentar en condiciones de alta pureza.
5. Todo gas tiene una isoterma crítica (para la cual T=Tc) que toca en un solo
punto la región bifásica del plano P-V, el punto crítico, cuyas coordenadas
________________________________________________________________________________________________
Capítulo 6. Sistemas Reales
7
son (Pc,vc), la presión y volumen molar críticos. En est punto se ubica el
punto de inflexión de la isoterma crítica, donde
Tal como se menciona en el punto 3 anterior, la isoterma estable es horizontal
cuando las fases líquida y de vapor están presentes, bajo la curva saturación del
líquido y la curva de saturación del vapor.
La ecuación de estado de van der Waals realiza incorpora las fuerzas atractivas
entre moléculas, disminuyendo la presión por debajo del valor ideal. Para tomar
en cuenta esta contribución, la presión se aumenta en un término de fuerza
atractiva a/V2:
El término 1/V2 se denomina “presión de cohesión” o “presión cohesiva”, corrige
las fuerzas atractivas intermoleculares de largo alcance. (Esas son las fuerzas
que producen la tensión superficial en los líquidos.) El término b o "covolumen",
corrige el volumen finito de los átomos o moléculas, o, más precisamente, las
fuerzas repulsivas de corto alcance que se producen cuando las nubes
electrónicas se comienzan a traslapar.
Los valores de a y b se encuentran tabulados en manuales y libros.
continuación se muestran algunos valores para estas constantes.
A
Tabla 1. Parámetros de la ecuación de van der Waals.
Gas a, Pa m6/mol2 b, m3/mol x 103
O2
0.1381
3.184
N2
0.1368
3.864
H2O
0.5542
3.051
CH4
0.2303
4.306
CO
0.1473
3.951
CO2
0.3658
4.286
NH3
0.4253
3.737
H2
0.0248
2.660
He
0.00346
2.376
La ecuación de estado de van der Waals entrega un ajuste bueno a razonable
para la mayoría de los gases. (Un mejor ajuste requiere distintos valores de a y/o
b en distintas regiones del plano P-V.) En las regiones correspondientes a
temperaturas bajo Tc y a presiones suficientemente altas para que ocurra la
condensación, la ecuación de van der Waals realmente predice el
________________________________________________________________________________________________
Capítulo 6. Sistemas Reales
8
comportamiento oscilatorio asociado a las fases metaestables y no la línea
horizontal P=cte. que realmente se encuentra mientras ocurren cambios de fase.
Las constantes a y b pueden asociarse fácilmente a los parámetros críticos del
gas: Pc, vc y Tc. Pero como hay solo dos constantes de van der Waals, ello
significa que existe una restricción entre los parámetros críticos. La precisión con
que esta condición se cumple en un determinado gas es una medida de la
validez de la ecuación de van der Waals para dicho gas. La relación con esta
restricción es la siguiente:
•
Hay que resolver la ecuación de van der Waals para P:
•
.
Hay que imponer que la pendiente se anule:
•
.
Hay que imponer que la curvatura se anule:
.
Estas últimas dos ecuaciones deben anularse simultáneamente en el punto
crítico (Pc,vc,Tc). De ellas se desprende que
o
Luego, resolviendo la primera ecuación para Tc,
o
Ahora, sustituyendo en la ecuación para P,
o
El valor que se deduce para la restricción es que:
.
________________________________________________________________________________________________
Capítulo 6. Sistemas Reales
9
Los datos experimentales muestras que la predicción que hace el modelo de van
der Waals es mucho más cercano que el que hace la ecuación del gas ideal,
aunque para ningún gas se obtiene una precisión mayor al 20%.
La ecuación de van der Waals predice la curva de inversión, la cual no se
desprende del modelo del gas ideal. Para observar este comportamiento
primero “reduciremos” la ecuación de van der Waals a su forma “reducida”, la
cual la hace universal y aplicable a todos los gases simultáneamente. Esto se
hace definiendo la presión reducida, el volumen molar reducido y la temperatura
reducida como sigue:
⇔
⇔
⇔
Por lo tanto, la ecuación de van der Waals ahora se ve ahora como
e inmediatamente se reduce a
Ecuación reducida
de van der Waals
Como puede observarse, la ecuación reducida de van der Waals es
independiente del gas(¡!), de manera que es posible hablar del gas de van der
Waals y no de un gas de van der Waals.
6.3.3 El coeficiente de Joule-Thomson del gas de van der Waals
El coeficiente de Joule-Thomson está definido por:
Al derivar la ecuación reducida de van der Waals con respecto a θ, manteniendo
πconstante
de manera que
y en consecuencia
________________________________________________________________________________________________
Capítulo 6. Sistemas Reales
10
.
La curva de inversión está definida por el lugar geométrico de los puntos (πi,φi,θi)
para los cuales µ= 0. Luego, de la forma de µ,
ahora la ecuación de van der Waals reducida es válida a lo largo de la curva de
inversión de la misma forma que en cualquier otro lugar, de manera que
y se ve que
o
Resolviendo la ecuación cuadrática:
Ahora podemos ubicar la curva de inversión en el plano P-V reducido:
• Cuando πi>9, no hay raíces reales (no hay inversión).
• Cuando πI=9, hay una raíz, en el volumen crítico φi=1, o v=vc.
• Cuando πi<9, dos raíces reales, que corresponden a las dos ramas de la
curva de inversión.
Las curvas de inversión normalmente se grafican en el plano T-P (equivalente al
plano θ-π), de manera que al sustituir de vuelta para encontrar θi en términos de
πi:
luego
Elevando al cuadrado se encuentran las dos ramas de la curva de inversión:
Es decir, las dos ramas se unen en πi=9, donde θi=3 y, como se vio
anteriormente, φi=1. Estas ramas unen este punto con el eje θ, donde se anula π,
en los puntos θi-=3/4 y θi+=27/4. Claramente es la región interior de esta curva
________________________________________________________________________________________________
Capítulo 6. Sistemas Reales
11
donde la ecuación de van der Waals predice que el estrangulamiento de un gas
producirá un enfriamiento.
La figura anterior compara las curvas de inversión reales del hidrógeno y del
nitrógeno con la predicción de la ecuación de van der Waals.
________________________________________________________________________________________________
Capítulo 6. Sistemas Reales
12