osciladores - U. T. F. S. M.

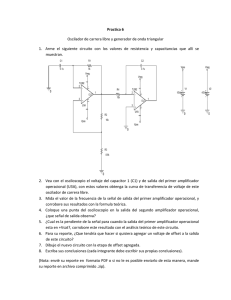
OSCILADORES
El uso de realimentación positiva que da por resultado un
amplificador realimentado que tiene ganancia de lazo cerrado |Af|
mayor que 1, y que si satisface las condiciones de fase producirá una
operación como la de un circuito oscilador. Un circuito oscilador
proporciona entonces una señal de salida que varía constantemente. Si
la señal de salida varía en forma senoidal, el circuito se denomina
oscilador senoidal. Si el voltaje de salida aumenta rápidamente a un
nivel de voltaje y después disminuye rápidamente a otro nivel de
voltaje, por lo general, el circuito se conoce como oscilador de pulsos o
de onda cuadrada.
Para comprender la manera en que funciona como oscilador un
circuito con realimentación considérese el circuito realimentado de la
figura 1. Cuando el interruptor en la entrada de amplificador está
abierto, no ocurre la oscilación. Considérese que tenemos un voltaje
ficticio en la entrada de amplificador (Vi). Este produce un voltaje de
salida Vo = Avi después de la etapa del amplificador, así como un voltaje
Vf = β(Avi) después de la etapa de realimentación. En consecuencia,
tenemos un voltaje de realimentación Vf = βAvi, donde βA se conoce
como la ganancia del lazo. Si los circuitos del amplificador y la red de
realimentación proporcionan βA de una magnitud y fase correctas, Vf
puede hacerse igual a Vi. Por consiguiente, cuando el interruptor está
cerrado y el voltaje Vi ficticio se suprime, el circuito continuará operando
ya que el voltaje de realimentación es suficiente para excitar el
amplificador y los circuitos de realimentación producen un voltaje de
entrada apropiado para sostener la operación del lazo. La forma de onda
de salida seguirá existiendo después de que el interruptor se cierre si la
condición se cumple.
βA = 1
(1)
+
Vi
-
Α
+
V0 = Α V i
-
β
+
Vf = β (Α Vi )
-
+ Vf = βΑ Vi -
Figura 1. Circuito de realimentación utilizado como
oscilador.
Esta se conoce como criterio de Barkhausen para la oscilación. En
realidad, no se requiere señal de entrada para activar el oscilador. Sólo
la condición βA = 1 debe cumplirse para que se produzcan oscilaciones
auto sostenidas. En la práctica βA se hace mayor que 1, y el sistema
empieza a oscilar amplificando el voltaje de ruido que siempre está
presente. Los factores de saturación en el circuito práctico proporcionan
un valor “promedio” de βA de 1. Las formas de onda que se producen
nunca son exactamente senoidales. Sin embargo, cuanto más cercano
sea el valor de βA a 1 tanto más próxima a una sinusoide será la forma
de onda. La figura 2 muestra cómo la señal de ruido da.
Envolvente de estado estacionario
limitada por la saturación del circuito
Oscilaciones no senoidales debido
a que βΑ no es exactamente 1
Forma de onda no senoidal
debido a la saturación
Figura 2. Establecimiento de osciladores de estado
estacionario.
Otra manera de ver cómo el circuito de realimentación brinda una
operación como oscilador se obtiene observando el denominador en la
ecuación de realimentación básica, Af = A/ (1 + βA). Cuando βA = -1 o
de magnitud 1 a un ángulo de fase de 180º, el denominador se vuelve 0
y la ganancia con realimentación, Af, se vuelve infinita. En esta forma,
una señal infinitesimal (voltaje de ruido) puede proporcionar un voltaje
de salida cuantificable, y el circuito actúa como oscilador incluso sin
señal de entrada.
El resto de este capítulo se dedica a diversos circuitos osciladores
que utilizan una variedad de componentes. Se incluyen las
consideraciones prácticas, por lo que se analizan los circuitos factibles
en cada uno de los diferentes casos.
Un ejemplo de un circuito oscilador que sigue el desarrollo básico
de un circuito de realimentación es el oscilador de desplazamiento de
fase. En la figura 3 se muestra una versión idealizada de este circuito.
Recuérdese que los requerimientos para la oscilación se basan en que la
ganancia de lazo, βA, sea mayor que la unidad y que el desplazamiento
de fase alrededor de la red realimentada sea de 180º (brindando
realimentación positiva). En la idealización presente estamos
considerando que la red realimentada será excitada por una fuente
perfecta (cero impedancia de la fuente) y que la salida de la red de
realimentación se conecta en una carga perfecta (impedancia de carga
infinita). El caso idealizado permitirá desarrollar la teoría detrás de la
operación del oscilador de desplazamiento de fase. Después se
considerarán las versiones prácticas de circuito.
Α
C
R
C
R
C
R
Red de retroalimentación
Figura 3. Oscilador de desplazamiento de fase idealizado.
Concentrando nuestra atención en la red de desplazamiento de
fase nos interesa la atenuación de la red a la frecuencia a la cual el
desplazamiento de fase es exactamente 180º. Empleando el análisis
clásico de red, encontramos que:
=
f
β
1
2π RC 6
=
1
29
(2)
(3)
y el desplazamiento de fase es 180º.
Para que la ganancia de lazo βA sea más grande que la unidad la
ganancia de la etapa del amplificador debe ser más grande que 1/β o
29.
A > 29
(4)
Al considerar la operación de la red con realimentación podrían
seleccionarse ingenuamente los valores de R y C para asegurar (a una
frecuencia específica) un desplazamiento de fase de 60º por sección
para tres secciones, produciéndose un desplazamiento de fase de 180º
como se desea. Sin embargo, éste no es el caso, puesto que cada
sección RC en la red de realimentación se carga menos que la anterior.
El resultado neto relativo a que el desplazamiento de fase total sea
180º, es lo más importante. La frecuencia dada por la ecuación (2), es
aquélla a la cual el desplazamiento de fase total es de 180º. Si se mide
el desplazamiento de fase por sección RC, cada sección no
proporcionaría el mismo desplazamiento de fase (aunque el
desplazamiento de fase completo es 180º). Si se hubiera deseado
obtener exactamente un desplazamiento de fase de 60º para cada una
de las tres etapas, entonces las etapas de emisor-seguidor serían
necesarias para cada sección RC con el fin de evitar que cada una fuera
cargada por el siguiente circuito.
Una versión práctica de un circuito oscilador de desplazamiento de
fase se muestra en la figura 4a. El circuito se dibujó para mostrar
claramente el amplificador y la red de realimentación. La etapa del
amplificador está auto polarizada con capacitor cortocircuitando la
resistencia de fuente Rs y un resistor de polarización del drenaje RD. Los
parámetros de interés del dispositivo FET son gm y rd. De la teoría del
amplificador FET la magnitud de la ganancia de amplificador se calcula a
partir de
|A| = gm RL
(5)
donde RL en este caso es la resistencia en paralelo de RD y rd.
=
RL
R D rd
R D + rd
(6)
Se supondrá como una muy buena aproximación, que la
impedancia de entrada de la etapa del amplificador FET es infinita. Esta
suposición es válida siempre y cuando la frecuencia de operación del
oscilador sea lo suficientemente baja, de manera que las impedancias
capacitivas del FET puedan despreciarse. La impedancia de salida de la
etapa de amplificador dada por RL debe ser también pequeña en
comparación con la impedancia vista hacia la red de realimentación de
manera que no ocurra atenuación debida a la carga. En la práctica,
estas consideraciones no siempre son despreciables, y la ganancia de la
etapa de amplificador se elige un poco mayor que el factor necesario de
29 para asegurar la acción de oscilación.
VDD
VCC
RD
RC
R1
gm . r d
R2
RS
C
R
C
R
RE
CS
C
R
R’
C
R
CE
C
R
C
Figura 4. Circuitos prácticos de oscilador de desplazamiento
de fase: (a) versión FET; (b) versión BJT.
EJEMPLO 1:
Se desea para diseñar un oscilador de desplazamiento de fase
(como en la figura 4a) un FET con los valores gm = 5000 µS, rd = 40 kΩ
, y un valor de circuito de realimentación R = 10 kΩ . Selecciónese el
valor de C para la operación del oscilador de 1 Khz. y RD para A > 29
con el fin de asegurar la acción del oscilador.
La ecuación (2) se emplea para encontrar el valor del capacitor.
Puesto que f = ½ π RC√6, podemos resolver para C:
C
=
1
=
2πRf 6
1
(6,28) (10 x10 ) (1x10 3 ) (2,45)
3
= 6,5nF
Empleando la ecuación (36), resolveremos RL para asegurar una
ganancia de, digamos, A = 40 (esto permita cierta carga entre RL y la
impedancia de entrada de la red de realimentación):
| A | = gm RL
RL
=
A
gm
=
40
500 x10 −6
= 8kΩ
Empleando la ecuación (37), resolveremos para RD = 10 kΩ.
Oscilador de desplazamiento de fase a transistor
Si se utiliza un transistor como elemento activo de la etapa del
amplificador, la salida de la red realimentada se carga de modo
apreciable mediante la resistencia de entrada relativamente baja (hie)
del transistor. Desde luego, podrá utilizarse una etapa de entrada del
emisor-seguidor seguida por una etapa de amplificador de emisor
común. Sin embargo, si se desea sólo una etapa de transistor resulta
más apropiado el empleo de una realimentación de voltaje en paralelo
(como se muestra en la figura 4b). En esta conexión, la señal de
realimentación se acopla a través del resistor de realimentación R’ en
serie con la resistencia de entrada de la etapa del amplificador (Ri).
El análisis del circuito de C.A. proporciona la siguiente ecuación
para la frecuencia del oscilador resultante:
(7)
Para que la ganancia de lazo sea mayor que la unidad, se
encuentra que el requerimiento sobre la ganancia de corriente del
transistor es:
h fe
> 23 + 29
R
Rc
+ 4
Rc
R
(8)
Oscilador de desplazamiento de fase de CI
A medida que los CI se han vuelto más populares, se han
adaptado para operar en circuitos osciladores. Se requiere sólo comprar
un amp-op para obtener un circuito amplificador de ganancia
estabilizada e incorporar algunos medios de realimentación de señal
para producir un circuito oscilador. Por ejemplo, en la figura 5 se
presenta un oscilador de desplazamiento de fase. La salida de un ampop se alimenta en una red RC de tres etapas que proporciona el
desplazamiento de fase necesario de 180º (a un factor de atenuación de
1/29). Si el amp-op brinda ganancia (fijada por los resistores Ri y Rf)
mayor que 29, resulta una ganancia de lazo mayor que la unidad y el
circuito actúa como oscilador [la frecuencia del oscilador está dada por
la ecuación 2].
Rf
+VCC
Ri
C
C
C
Amp-Op
+
R
R
R
-VEE
Figura 5. Oscilador de desplazamiento de la fase empleando
amp-op.
OSCILADOR DE PUENTE DE WIEN
Un circuito oscilador práctico utiliza un amp-op y un circuito
puente RC, con la frecuencia del oscilador fijada por los componentes R
y C. La figura 6 muestra una versión básica de un circuito oscilador de
puente de Wien. Obsérvense las conexiones básicas del puente. Los
resistores R1 y R2, y los capacitores C1 y C2 forman los elementos de
ajuste de frecuencia, en tanto que los resistores R3 y R4 forman parte
del circuito de realimentación. La salida del amp-op está conectada
como la entrada del puente en los puntos a y c. La salida del circuito
puente en los b y d es la entrada para el amp. op.
C1
R1
-
R2
C2
+VCC
R3
Amp-Op
R4
Señal
senoidal
de salida
+
-VEE
Figura 6. Circuito oscilador de puente de Wien empleando
un amplificador operacional.
Despreciando los efectos de carga de las impedancias de entrada y
salida del amp-op, el análisis del circuito puente produce.
R3
R4
=
y
fo
=
R1
R2
+
C2
C1
1
2π R1C1 R2 C2
(9)
(10)
En particular, si los valores son R1 = R2 = R y C1 = C2 = C, la
frecuencia del oscilador que resulta es:
fo
y
=
1
2πRC
(11)
(12)
De tal modo una relación de R3 con R4 mayor que 2 producirá la
suficiente ganancia de lazo en el circuito para que oscile a la frecuencia
calculada empleando la ecuación (11).
EJEMPLO 2.
Calcule la frecuencia resonante del oscilador de puente de Wien de
la figura 7.
+VCC
0.001 µF
+
51 kΩ
51 kΩ
Salida
Amp-Op
0.001 µF
-VEE
300 kΩ
100 kΩ
Figura 7. Circuito oscilador de puente de Wien para el
ejemplo 8.
Solución:
Utilizando la ecuación 42 se obtiene:
fo
=
1
2πRC
=
1
2π (51x10 ) (0,001x10− 6 )
3
= 3120,7 Hz
EJEMPLO 3.
Diseñe los elementos RC de un oscilador de puente de Wien como
en la figura 7 para que opere a fo = 10 Khz.
Solución:
Empleando valores iguales de R y C podemos elegir R = 100 kΩ y
calcular el valor requerido de C empleando la ecuación (42):
C
=
1
2πf o R
=
1
6,28(10 x103 )(100 x103 )
10 −9
=
6,28
= 159 pF
Podemos utilizar R3 = 300 kΩ y R4 = 100 kΩ para producir una
relación R3 / R4 mayor que 2 de modo que ocurra la oscilación.
CIRCUITO OSCILADOR SINTONIZADO
Circuitos osciladores de entrada y salida sintonizada
Diversos circuitos pueden construirse utilizando como referencia el
que se muestra en la figura 28 si se brinda sintonización tanto en la
sección de entrada como en la de salida del circuito. El análisis del
circuito de la figura 28 revela que se obtienen los siguientes tipos de
osciladores cuando los elementos de reactancia son como se designan:
Amplificador
X2
X1
X3
Figura 8. Configuración básica de un oscilador de circuito
resonante.
TIPOS DE OSCILADOR
ELEMENTOS DE REACTANCIA
X1
X2
X3
Oscilador Colpitts
C
C
L
Oscilador Hartley
L
L
C
LC
-
Entrada
sintonizada,
salida LC
sintonizada
Osciladores Colpitts
Oscilador COLPITTS Con FET
En la figura 29 se muestra una versión práctica de un oscilador
Colpitts con FET. El circuito presenta básicamente la misma forma como
la que se muestra en la figura 28 con la adición de los componentes
necesarios para la polarización DC del amplificador FET. Se encuentra
que la frecuencia del oscilador es:
fo
1
=
2π LC eq
(13)
donde:
C eq
=
C1C 2
C1 + C 2
(14)
VDD
RFC
Vo
CC
RG
C1
C2
L
Figura 9. Oscilador Colpitts con FET
Oscilador COLPITTS a Transistor
Un circuito oscilador Colpitts a transistor puede construirse como
se ilustra en la Figura 10. La frecuencia de oscilación del circuito está
dada por la ecuación 13.
VCC
RFC
C1
L
R1
Vo
C2
Cc
R2
RE
CE
Figura 10. Oscilador Colpitts a Transistor
Oscilador COLPITTS con CI
En la Figura 11 se presenta un oscilador Colpitts con amp-op.
También en este caso, el amp-op proporciona la amplificación básica
que se requiere, en tanto que la frecuencia del oscilador se fija mediante
una red de realimentación LC de configuración Colpitts. La frecuencia del
oscilador está determinada por la ecuación (13).
Rf =100 kΩ
+VCC
Ri =10 kΩ
Salida
Amp-Op
+
-VEE
C2
C1
L
Figura 11. Oscilador Colpitts con amp-op
Oscilador Hartley
Si los elementos en el circuito resonante básico de la Figura 8 son
X1 y X2 (inductores) y X3 (capacitor), el circuito es un oscilador Hartley.
Oscilador HARTLEY con FET
En la Figura 12 se muestra un circuito oscilador Hartley con FET. El
circuito está dibujado de modo que la red de realimentación integre la
forma que se muestra en el circuito resonante básico (Figura 8). Sin
embargo, nótese que los inductores L1 y L2 tienen un acoplamiento
mutuo. M, que debe considerarse en la determinación de la inductancia
equivalente para el circuito tanque resonante. La frecuencia de
oscilación del circuito se aproxima mediante:
fo
1
=
(15)
2π Leq C
como:
Leq = L1 + L2 + 2 M
(16)
Oscilador HARTLEY a Transistor
La Figura 30 muestra un circuito oscilador Hartley a transistor. El
circuito opera a una frecuencia determinada por la ecuación (15).
VCC
+VDD
RFC
Cc
CG
L1
RG
Cicuíto tanque
RFC
Cc
R1
C
L1
L2
Vo
CL
L2
M
R2
RE
CE
C
Figura 12. Oscilador Hartley con
Hartley FET
Figura 13. Circuito oscilador
a transistor.
OSCILADOR DE CRISTAL
Un oscilador de cristal consiste básicamente en un oscilador de
circuito sintonizado que utiliza un cristal piezoeléctrico como circuito
tanque resonante. El cristal (usualmente de cuarzo) tiene una mayor
estabilidad en cuanto a mantenerse constante a cualquier frecuencia a al
cual se corte originalmente el cristal para operar. Los osciladores de
cristal se usan siempre que se requiere gran estabilidad; por ejemplo,
en transmisores y receptores de comunicaciones.
Un cristal de cuarzo (uno de los diversos tipos de cristal) presenta
la propiedad de que cuando se aplica un esfuerzo mecánico entre sus
caras, se genera una diferencia de potencial a través de las caras
opuestas del mismo. Esta propiedad de un cristal se denomina efecto
piezoeléctrico. En forma semejante, un voltaje aplicado a través de un
conjunto de caras de cristal ocasiona distorsión mecánica en la forma de
cristal.
Cuando se aplica voltaje alterno en un cristal, se establecen
vibraciones mecánicas (estas vibraciones tienen una frecuencia
resonante natural que depende del cristal). Aunque el cristal tiene
resonancia electromecánica, podemos representar su acción mediante
un circuito resonante eléctrico equivalente, como se muestra en la figura
31. El inductor L y el capacitor C representan equivalentes eléctricos de
la masa del cristal, en tanto que la resistencia R es un equivalente
eléctrico de la fricción interna de la estructura del cristal. La capacitancia
en paralelo CM representa la capacitancia debida al montaje mecánico
del cristal. Puesto que las pérdidas en el cristal, representadas por R,
son pequeñas, el Q equivalente del cristal (factor de calidad) es alto; por
lo común de 20.000. Pueden alcanzarse valores de Q casi de hasta 106
empleando cristales.
R
L
CM
C
Figura 14. Circuito equivalente eléctrico de un cristal.
El cristal como el que se representa mediante el circuito eléctrico
equivalente de la figura 14, puede tener dos frecuencias resonantes.
Una condición resonante ocurre cuando las reactancias de la rama RLC
en serie son iguales (y opuestas). Para esta condición la impedancia
resonante en serie es muy baja (igual a R). La otra condición resonante
ocurre a una frecuencia más elevada cuando la reactancia de la rama
resonante en serie iguala la reactancia del capacitor CM. Esta es una
condición de resonancia o antirresonancia en paralelo del cristal. A esta
frecuencia el cristal ofrece una impedancia muy alta al circuito externo.
La impedancia frente a la frecuencia del cristal se muestra en la figura
15. Con el objeto de emplear el cristal de manera apropiada debe
conectarse en un circuito de manera que se elija su impedancia baja en
el modo de operación de resonancia en serie o el de impedancia alta en
el modo de operación antirresonante.
|Z|
0
f1
f2
(resonancia en serie) (antirresonancia)
Figura 15. Impedancia del cristal contra la frecuencia.
Circuitos resonantes en serie
Para excitar un cristal para operación en el modo resonante en
serie puede conectarse como un elemento en serie en un circuito de
realimentación. En la frecuencia resonante en serie del cristal su
impedancia es más pequeña y la cantidad de realimentación (positiva)
es más grande. En la figura 16 se muestra un circuito a transistor
común. Los resistores R1, R2 y RE proporciona un circuito de polarización
de DC estabilizado por divisor de voltaje. El capacitor CE cortocircuita a
CA la resistencia del emisor y las bobinas RFC proporcionan polarización
de DC en tanto que desacoplan cualquier señal CA en las líneas de
alimentación para que no afecten la señal de salida. La realimentación
de voltaje de colector a base es un máximo cuando la impedancia del
cristal es mínima (en el modo resonante en serie). El capacitor de
acoplamiento CC tiene una impedancia despreciable a la frecuencia de
operación del circuito, pero bloquea cualquier DC entre el colector y
base.
VCC
VDD
R1
‚
RFC
CC
RFC
CRISTAL
Salida
CRISTAL
‚
Salida
CC
RG
R2
RE
(a)
CE
(b)
Figura 16. Oscilador controlador por cristal utilizando un
cristal en resonancia serie en el circuito de
realimentación serie (a) circuito BJT; (b)
Circuito FET.
La frecuencia de oscilación resultante del circuito se obtiene
mediante la frecuencia de resonancia serie del cristal. Los cambios en el
voltaje de la fuente, los parámetros del dispositivo transistor, etc., no
tienen efecto sobre la frecuencia de operación del circuito la cual se
mantiene estabilizada por medio del cristal. La estabilidad de frecuencia
del circuito se fija mediante la estabilidad de frecuencia del cristal, que
es adecuada.
Circuitos resonantes en paralelo
Puesto que la impedancia resonante en paralelo de un cristal es un
valor máximo, se encuentra conectada en paralelo. A la frecuencia de
operación resonante en paralelo, un cristal aparece como una reactancia
inductiva de valor más grande. La Figura 17 muestra un cristal
conectado como el elemento inductor en un circuito Colpitts modificado.
El circuito de polarización de DC básico debe ser evidente. Se desarrolla
el voltaje máximo a través del cristal a su frecuencia resonante en
paralelo. El voltaje de acopla en el emisor por medio de un divisor de
voltaje de capacitores: capacitores C1 y C2.
VCC
R1
RFC
Salida
C1
CB
R2
RE
C2
‚
CRISTAL
Figura 17. Oscilador controlado por cristal operando en
resonancia paralelo.
Un circuito oscilador Muller controlado por cristal se presenta en la
figura 18. Se coloca un circuito LC sintonizado en la sección de drenaje y
se ajusta cerca de la frecuencia resonante en paralelo del cristal. La
señal de compuerta-fuente máxima ocurre a la frecuencia
antirresonante del cristal que controla la frecuencia de operación del
circuito.
VDD
L
C
Salida
CRISTAL
‚
RG
RFC
RS
CS
Figura 18. Oscilador Miller controlado por cristal.
Oscilador a cristal.
Puede emplearse un amp-op en un oscilador cristal como se ilustra
en la figura 19. El cristal se conecta en el circuito resonante en serie y
opera a la frecuencia resonante en serie del cristal. El circuito presente
tiene una alta ganancia de manera que se produce una señal de onda
cuadrada de salida como se indican en la figura. En la figura se incluyen
un par de diodos Zener en la salida para proporcionar una amplitud de
salida exactamente al voltaje del Zener (VZ).
Rf
100 kΩ
+VCC
Ri
1 kΩ
-
VZ
0V
Amp-Op
+
-VEE
VZ
CRISTAL
100 kΩ
‚
0.1 µF
Figura 19. Oscilador de cristal que utiliza un amp-op.
Oscilador Monounión
Un dispositivo particular, el transistor monounión puede emplearse
en un circuito oscilador de una sola etapa para producir una señal de
pulso apropiada en las aplicaciones de circuitos digitales. El transistor
monounión puede utilizarse en lo que se denomina oscilador de
relajación, como se muestra en el circuito básico de la figura 20. El
resistor RT y el capacitor CE son los componentes temporizadores que
fijan la frecuencia de oscilación del circuito. La frecuencia de oscilación
puede calcularse empleando la ecuación (17), que incluye la relación de
apagado intrínseca del transistor monounión η, como un factor (además
de RT y CT) a la frecuencia de operación del oscilador.
VBB
RT
VE
R2
B2
B1
CT
VB2
VB1
R1
Figura 20. Circuito oscilador monounión básico.
(17)
Típicamente, un transistor monounión tiene una relación de
apagado de 0,4 a 0,6. Empleando un valor de η = 0,5, obtenemos:
(18)
El capacitor CT se carga a través del resistor RT hasta el voltaje de
alimentación VBB. Mientras el voltaje de capacitor VE esté por abajo del
voltaje de disparo (VP) fijado por medio del voltaje entre B1 - B2, y la
relación de apagado del transistor η.
VP = η VB1 VB2 - VD
(19)
La conexión del emisor monounión aparece como circuito abierto.
Cuando el voltaje del emisor a través del capacitor CT excede este valor
(VP), el circuito monounión se dispara, descargando el capacitor,
después de lo cual se inicia un nuevo ciclo de carga. Cuando se dispara
el monounión, se genera un aumento de voltaje en R1 y la caída de
voltaje se desarrolla en Rw como se ilustra en al figura 21. La señal en el
emisor es una forma de onda de voltaje diente de sierra, que en la base
1 es un pulso en sentido positivo, y que en la base 2 es un pulso en
sentido negativo. En la Figura 22 se presentan ciertas variaciones del
circuito oscilador monounión.
VBB
VE
VE = VP
VEmín
0V
Tiempo
VB1
0V
VB2
Tiempo
0V
Tiempo
Figura 21. Formas de onda del oscilador monounión.
VBB
VBB
RT
RT
R2
CT
R1
(a)
RT
VBB
(b)
R2
RC
Vsalida
RB
CT
R1
(c)
Figura 22. Algunas configuraciones del circuito oscilador
monounión.
PROBLEMAS:
Tipos de conexión de realimentación:
1. Calcule la ganancia de un amplificador con realimentación
negativa que tiene A = 2.000, β = -1/10.
2. Si la ganancia de un amplificador cambia a partir de un valor de
1000 en 10%, calcule el cambio en la ganancia si en el amplificador se
emplea un circuito de realimentación en el que β = -1/20.
3. Calcule la ganancia y las impedancias de entrada y salida de un
amplificador con realimentación de voltaje en serie que tiene A = -300,
Ri = 1,5 kΩ , Ro = 50 kΩ y β = -1/15.
Circuito de realimentación prácticos:
4. Calcule la ganancia con y sin realimentación en un amplificador
FET como el de la figura 5, para valores de circuito R1 = 800 kΩ, R2 =
200 kΩ , Ro = 40 kΩ , RD = 8 kΩ y gm = 500 µS.
5. En un circuito como el de la Figura 11 con los siguientes
valores, calcule la ganancia y la impedancia de entrada y salida del
circuito con y sin realimentación: RB = 600 kΩ , RE = 1,2 kΩ, RC = 4,7
kΩ y β = 75. Use VCC = 16 V.
Oscilador de desplazamiento de fase:
6. Un oscilador de desplazamiento de fase que tiene gm = 6.000
µS, rd = 36 kΩ y resistor de realimentación R = 12 kΩ operará a 2,5
Khz. Elija C para la operación especificada del oscilador.
7. Calcule la frecuencia de operación de un oscilador BJT de
desplazamiento de fase, como en la figura 4b, para R = 6 kΩ , C = 1500
pF y RC = 18 kΩ.
Oscilador de puente de Wien:
8. Calcule la frecuencia de un circuito oscilador de puente de Wien
(como el de la figura 6) cuando R = 10 kΩ y C = 2400 pF.
Circuito oscilador sintonizado:
9. Para el oscilador Colpitts con FET de la Figura 9 y los siguientes
valores de circuito, determine la frecuencia de oscilación: C1 = 750 pF,
C2 = 2500 pF, L = 40 µH.
10. Para el oscilador Colpitts transistorizado de la Figura 10 y los
siguientes valores de circuito, calcule la frecuencia de oscilación: L =
100 µH, LRFC = 0,5 mH, C1 = 0,005 µ F C2 = 0,01 µ F, CC = 10µ.
11. Calcule la frecuencia del oscilador en un oscilador Hartley con
FET como el de la figura 12 para los siguientes valores de circuito: C =
250 pF, L1 = 1,5 mH, L2 = 1,5 mH, M = 0,5 mH.
12. Calcule la frecuencia de oscilación en el circuito Hartley
transistorizado de la figura 13 los siguientes valores circuito: LRFC = 0,5
mH, 750 µ H, L2 = 750 µH. M = 150 µH, C = 150 pF.
Oscilador a cristal
13. Dibujo los diagramas de circuito de (a) un oscilador de cristal
operado en serie y (b) un oscilador de cristal excitado en paralelo.
Oscilador monounión:
14. Diseñe un circuito oscilador monounión para operación a (a) 1
Khz. y (b) 150 Khz.