10 densidad de estados. El espectro de la red

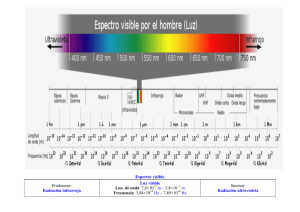
FES. Densidad de estados. El espectro de la red
Al igual que en la teoría de electrones en una red estática para el cálculo de propiedades
vamos a necesitar determinar el espectro energético de la red. Es decir evaluar el numero
de valores ω(q) que caen dentro de un intervalo dω.
El planteamiento de este problema es el siguiente:
Llamemos Dj(ω) dω al número de modos normales de vibración con energías comprendidas
entre ω y ω+dω. Donde el sub-índice j hace referencia a la rama número j.
Así en una red tridimensional con n-átomos por celdilla debe cumplirse la relación:
3
Donde ωmax es la frecuencia máxima de la red o frecuencia de corte
FES. Densidad de estados. El espectro de la red
Para determinar D(ω) dω debemos usar tres ecuaciones:
1. La relación de dispersión de la red ω (q)
2. La expresión para la densidad de estados en función de la dimensión del sistema
Para 1D
2
2
Donde La es la longitud del cristal y L el número de celdillas
Para 2D
4
Donde S es la superficie del cristal
Para 3D
8
Donde V es el volumen del cristal
3. En ocasiones será necesario usar la definición de D(ω ) para encontrar ωmax
FES. Densidad de estados. El espectro de la red
Cadena lineal mono-atómica con un átomo por celdilla.
2
2
FES. Densidad de estados. El espectro de la red
FES. Densidad de estados. El espectro de la red
Espectro de la red para una cadena lineal mono-atómica
FES. Densidad de estados. El espectro de la red
Cadena lineal con dos átomo por celdilla.
Al haber dos átomos por celdilla hay dos modos de vibración
FES. Densidad de estados. El espectro de la red
Y por tanto el espectro de la red se desdobla en dos, una para cada uno de los
modos de vibración (acústico y óptico)
Hacer este cálculo como
ejercicio
FES. Densidad de estados. El espectro de la red
Como el cálculo exacto del espectro de la red puede resultar complejo existen varios modelos
aproximados para dar cuenta del mismo (Modelo de Debye, de Einstein e hibrido Debye-Einstein).
Más adelante veremos como estas aproximaciones a la realidad pueden ser usadas en el cálculo de las
propiedades del sólido asociadas a los grados de libertar de los cores.
Sólido 3D genérico