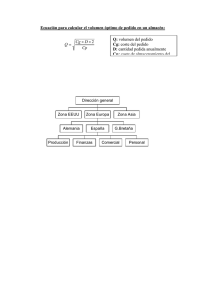
unidades Q 250 07,0250,0 1000 202 = × + × × = i QPQ AQD

Salchiburguer, restaurante de comida rápida es conocido por su pan especial para
hamburguesas. Salchiburger compra anualmente 1.000 unidades de panecillos a un
precio de 2 € cada uno. EL mantener almacenada una unidad de producto le supone
un coste anual de 0,50 €..El coste de realización de pedidos asciende a 20 € .
Además, se sabe que el proveedor que suministra los pedidos tardea 10 días en
servirlos, y por último, se sabe que el coste del capital es del 7%, Con estos datos
calcular:
a)
b)
c)
d)
El volumen óptimo de unidades por pedido.
Coste total del inventario
Número esperado de pedidos
Teniendo en cuenta que 300 es el número de días que la empresa trabaja
al año, cuál será el tiempo esperado entre pedidos
e) El consumo diario del pan especial
f) Teniendo en cuenta que el proveedor tarda 4,5 días en servir el pedido.
Cuántas unidades de pan debe contener el almacén en el momento de
solicitar cada pedido para asegurarse de por un lado satisfacer la demanda
y por otro que el almacén se vacíe en el mismo momento en que llega el
pedido solicitado.
a) Para calcular el volumen óptimo de un pedido es utilizamos la siguiente
expresión:
Q=
2 ED
A+ P×i
Sustituyendo los datos del ejemplo obtenemos:
Q=
2 × 20 × 1000
= 250 unidades
0,50 + 2 × 0,07
b) El coste total del inventario se calcula aplicando la siguiente fórmula:
CT = Ca + Cr + Cal + C f = D × P + E ×
D
Q P×Q
+A +
×i
Q
2
2
Sustituyendo obtenemos:
CT = 1.000 × 2 + 20 ×
1.000
250 2 × 250
+ 0,50
+
× 0,07 = 2.160 €
2
2
250
c) Para calcular el número esperado de pedidos dividimos a la demanda (D) entre
el volumen óptimo (Q):
Número Esperado de pedidos =
1.000
= 4 pedidos
250
d) El tiempo esperado entre cada pedido se calcula dividiendo al número de días
de trabajo al año entre el número esperado de pedidos
Tiempo esperado entre pedidos =
300
= 75 días
4
e)
Dividiendo la demanda total de pan entre el número de días laborables de la
empresa se obtiene las unidades diarias que se consumen:
1.000
= 3,33 unidades que se consumen al día
300
f)
Teniendo en cuenta que cada día se consumen 3, 33 unidades de pan y
sabiendo que el proveedor tarda 4,5 días en servir el pedido, resulta
evidente que habrá que formular un pedido cuando el almacén contenga:
4,5 × 3,33 = 15 unidades
Ya que si se consumen más unidades puesto que el proveedor tarde cuatro
días y medio en servirnos, antes de que llegue el nuevo pedido el almacén
se habrá quedado vacío y no podremos atender a la demanda.
El proveedor que suministra el pan especial para hamburguesas al restaurante de
comida rápida anterior ofrece a su dueño un descuento en función de la cantidad
pedida. Recordemos que el precio unitario del pan es de 2 € , pero para pedidos entre
300 y 499 unidades el proveedor aplicará un precio por unidad de 1,50 € y para
pedidos iguales o mayores a las 500 unidades el precio de cada pan será de 1 €,
siendo el coste de almacenamiento el 10% de su precio. Utilizando el resto de datos
como en el ejemplo anterior excepto el valor de E = 15 €, ¿cuál será la cantidad de
pedido que minimiza el coste total del inventario?
Para resolverlo se deberá utilizar el modelo de descuento por cantidad para ello:
a) Se calcula la cantidad de pedido para cada uno de los precios
Q1 =
Q2 =
Q3 =
2 × 15 × 1.000
= 297 unidades
0,10 × 2 + 2 × 0,07
2 ED
=
IP + Pi
2 × 15 × 1.000
= 343 unidades
0,10 × 1,5 + 1,5 × 0,07
2 ED
=
IP + Pi
2 ED
=
IP + Pi
2 × 15 × 1.000
= 420 unidades
0,10 × 1 + 1 × 0,07
b) Si la cantidad de pedido es demasiado baja para la aplicación del descuento se
ha de redondear al alza el valor de Q hasta la cantidad más baja que permita el
descuento.
- Como Q1 está entre 0 y 299 no se tiene que ajustar el valor de Q
- Como Q2 se encuentra en el intervalo 300 -500 no se tiene que ajustar el valor
de Q
- Como Q está por debajo de las 500 unidades hay que ajustar el valor de Q
hasta 500 unidades
Q1 = 297 unidades
Q2 = 343 unidades
Q3 = 500 unidades (ajustado)
c) Calcular el coste total del inventario para cada una de las cantidades de pedido
utilizando la siguiente ecuación:
CT = Ca + Cr + Cal + C f = D × P + E ×
CT1 = 1.000 × 2 + 15 ×
D
Q P×Q
+A +
×i
Q
2
2
1.000
297 2 × 297
+ 0,10 x 2 x
+
× 0,07 = 2.101 €
297
2
2
CT2 = 1.000 × 1,5 + 15 ×
1.000
343 1,5 × 343
+ 0,10 x1,5 x
+
× 0,07 = 1.587,46 €
343
2
2
CT 3 = 1 . 000 × 1 + 15 ×
1 . 000
500 1 × 500
+ 0 ,10 × 1
+
× 0 , 07 = 1 . 072 ,5 €
500
2
2
d) Seleccionar la cantidad de pedido que haga mínima la función de costes
anterior
De esta manera, la cantidad de pan que habrá de pedirse será d 500 unidades,
ya que esta cantidad es la óptima al minimizar la función de coste total del
inventario
Q = 500 unidades