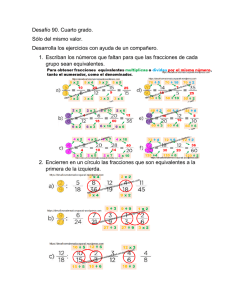
= → + = 3,075 Para que las fracciones sigan siendo equivalentes si
Anuncio

= , → + = 3,075 Para que las fracciones sigan siendo equivalentes si multiplicamos o dividimos el denominador por un número debemos multiplicar o dividir también el numerador por el mismo número. 2,1 ÷ 2 = 1,05 Por tanto, para que las fracciones sigan siendo equivalentes + = 1,05 = 3,075 Sustituimos y popr su valor en función de x + 1,05 = 3,075 2,05 = 3,075 = 3,075 ÷ 2,05 = 1,5 Ahora calculamos el valor de y = 1,05 = 1,05 ∗ 1,5 = 1,575 Soluciones: c) x=1,5 c) y=1,575 6 = 21 = 15 → + + = 56 Usamos el mismo planteamiento que en el ejercicio anterior = → = = → = + + → lo pedemos expresar también en función de x→ + = 56 + = 56 = 56 14 + 49 + 35 = 56 ∗ 14 98 = 784 = 784 ÷ 98 =8 Solución: d) x=8 = ∗ =