A continuación cada ejercicio tiene un valor de 10 puntos si está

Segundo Parcial
Computación 1
Julio 2016
A continuación cada ejercicio tiene un valor de 10 puntos si está todo correcto, 0 si esta incorrecto o
incompleto. Los ejercicios deben realizarse en una hoja aparte, las mismas deben identificarse con Nombre
completo y Cédula de Identidad.
Ejercicio 1 (Ejercicio 11, práctico 5)
Considere la función f tal que f(x) = x2- 18x + 5, donde x es un valor entero en la escala de -10 a 10. Escriba
un programa en Octave que encuentre y despliegue el valor máximo de f(x) para x en ese entorno.
% Código Octave
% Defino la función f a evaluar, f(x) = x^2-18x+5
function valor = f(x)
valor = x^2 - 18*x + 5;
endfunction
%Código del programa que resuelve el problema
maximo = 0 % esta variable almacenará el máximo calculado, se incializa en 0
% esta iteración calcula la funcion para todos los enteros de (-10,10)
for i=-10:10
y = f(i)
% si el valor calculado es mayor que el que consideramos máximo, este ultimo se actualiza
if (y > maximo)
maximo = y;
endif
endfor
% mostramos el máximo calculado
disp("El máximo es:")
maximo
Ejercicio 2 (Ejercicio 16, práctico 5)
Escriba un programa en Octave que determine si un número n es primo, n es un entero positivo leído de la
entrada estándar.
% Código Octave
%pido que ingresen el numero
n = input("Ingrese un entero positivo n (n>0)")
% si n es 1, ya sabemos que es primo
if (n==1)
disp("Ingreso el número 1, es primo");
else %si no
i = 2;
parar = false; %variable para detener el ciclo una vez que detectamos que n es divisible entre algun i
while (i < n && not(parar))
if (rem(n,i) == 0)
disp("El numero ingresado no es primo, es divisible entre")
i
1 de 2
Segundo Parcial
Computación 1
Julio 2016
parar = true;
endif
i = i + 1;
endwhile
if not(parar)
disp("El numero ingresado es primo")
endif
endif
Ejercicio Opcional (en caso de resolver bien este ejercicio, se agregara 20 puntos a la nota final del
Segundo Parcial)
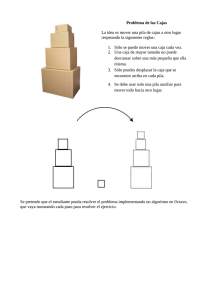
Problema de las Cajas
La idea es mover una pila de cajas a otro lugar respetando la siguientes
reglas:
1. Sólo se puede mover una caja cada vez.
2. Una caja de mayor tamaño no puede descansar sobre una más
pequeña que ella misma.
3. Sólo puedes desplazar la caja que se encuentre arriba en cada pila.
4. Se debe usar solo una pila auxiliar para mover todo hacia otro lugar.
Se pretende que el estudiante pueda resolver el problema implementando un algoritmo en Octave, que vaya
mostrando cada paso para resolver el ejercicio.
Este problema se conoce tambien como las torres de Hanoi: https://es.wikipedia.org/wiki/Torres_de_Han
%C3%B3i. Se deben considerar tres pilas de cajas (la de origen, la auxiliar y la final)
Un código que resuelve el problema para las cajas recursivamente es este:
function cajas( cantCajas,com,aux,fin )
if cantCajas==1
fprintf('mover caja de arriba de %s a %s',com,fin);
else
cajas(cantCajas-1,com,fin,aux);
fprintf('\nmover caja de arriba de %s a %s\n',com,fin);
cajas(cantCajas-1,aux,com,fin);
end
endfunction
n=input('Numero de cajas: ');
fprintf('Los movimientos a realizar son: \n');
cajas(n,"pila origen","pila aux","pila final");
fprintf('\n');
2 de 2