Átomo aislado Molécula Red periódica Banda prohibida EC EV EG

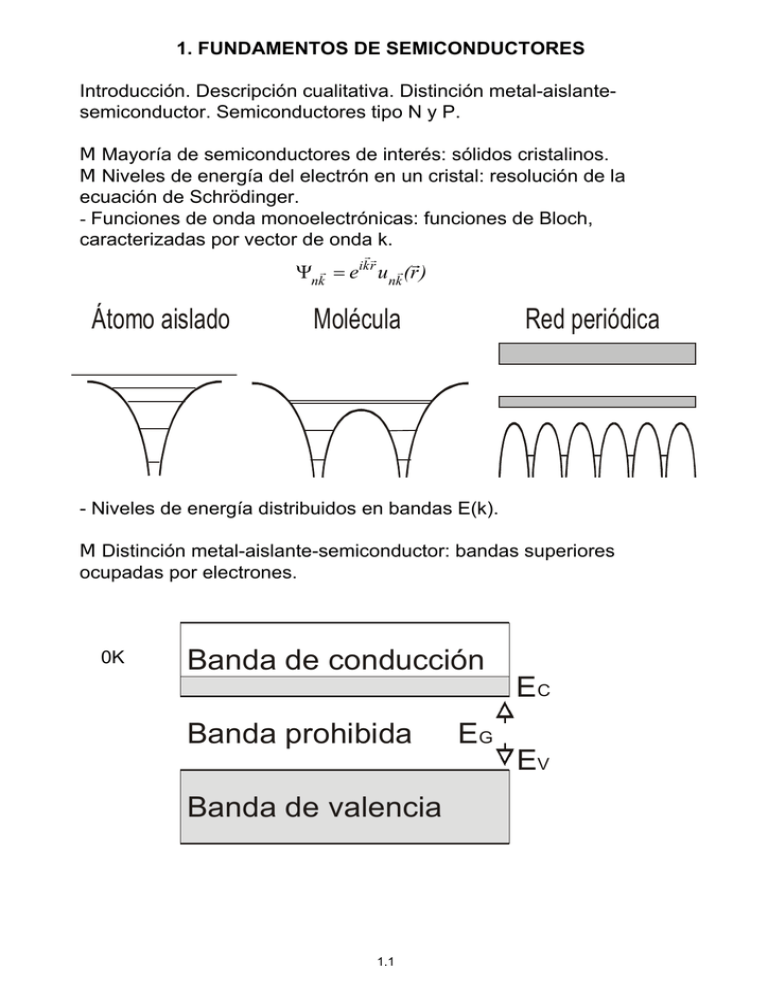
1. FUNDAMENTOS DE SEMICONDUCTORES
Introducción. Descripción cualitativa. Distinción metal-aislantesemiconductor. Semiconductores tipo N y P.
M Mayoría de semiconductores de interés: sólidos cristalinos.
M Niveles de energía del electrón en un cristal: resolución de la
ecuación de Schrödinger.
- Funciones de onda monoelectrónicas: funciones de Bloch,
caracterizadas por vector de onda k.
rr
ik r
r
Ψnkr = e unkr(r )
Átomo aislado
Molécula
Red periódica
- Niveles de energía distribuidos en bandas E(k).
M Distinción metal-aislante-semiconductor: bandas superiores
ocupadas por electrones.
0K
Banda de conducción
Banda prohibida
Banda de valencia
1.1
EG
EC
EV
M 0K
Aislantes y
semiconductores
Metales
EC
EG
EC
EG
EV
EV
Conducción por electrones
No conducción
M T>0, T.ambiente
EC
F.0
F>0
EG
Semiconductor.
Conducción por
e- y huecos
EG
EV
Aislante
EC
EV
M Diferencia metal-semiconductor por vía experimental:
- Dependencia térmica de σ
F
F
T
T
Semiconductor
Metal
- Por el signo de los portadores de carga medido por efecto Hall.
M Modelo de enlace covalente.
Concepto de HUECO.
Si
Si Si
2
1.2
Si
Si
1
EFECTO HALL
Conducción por electrones.
B
E
v
-q·E
-
J
EH
Campo
resultante
-q·vvB
Acumulación de
electrones
F = -qE - qv ∧ B
Conducción por huecos.
E
B
v +
q·E
J
q·vvB
Acumulación de
huecos
1.3
EH
Campo
resultante
SEMICONDUCTORES TIPO N
Ejemplo: Silicio dopado con fósforo en posición sustitucional
Si
Si P
EC
ED
-
Si
Si
EV
- Ión fijo positivo Y Impureza donadora
- Se crean electrones sin huecos Y n>p
Y
- semiconductor tipo N
- conducción mayoritaria por electrones
electrones: mayoritarios.
huecos: minoritarios
SEMICONDUCTORES TIPO P
Ejemplo: Silicio dopado con boro en posición sustitucional
EC
Si
Si
B
Si
Si
-
EA
EV
- Boro ionizado fijo positivo Y Impureza aceptadora
- Se crean huecos sin electrones Y p>n
Y
- semiconductor tipo P
- conducción mayoritaria por huecos
huecos: mayoritarios.
electrones: minoritarios
1.4
Electrón libre:
dp d( hk)
=
= ma
dt
dt
F = -qE =
2
E=
Electrón en cristal:
2
p
=h k
2m
2m
F = -qE + F int = ... = ma
dp*
¿¿ - qE = m a =
??
dt
2
*
E
E
EC
EV
k
k
100
000
2
1 E
E(k) = E( k 0 ) + d 2 (k - k 0 )2 + ..
2 dk
CONCEPTO DE MASA EFECTIVA
Si los electrones y huecos se sitúan en torno a los extremos de las
bandas podemos desarrollar E(k) respecto a ellos. En primera
aproximación tenemos unas bandas parabólicas:
En( k n )= Ec +
2
h 2 ( k n - k min )
2 m*n
+ ...
2
h2 k p
+ ...
E p( k p )= Ev +
2 m*p
Definición p n = h( k n - k min )
⇒
cuasimomento :
p p = hk p
p 2n
En = Ec +
2 m*n
E p = Ev +
p 2p
2 m*p
1 dE
1 dE
d( hk)
; dE = F ext vdt = F ext
dt; F ext =
dt
h dK
h dk
dv 1 d  dE  1 d 2 E dk 1 d 2 E
a= =
= 2
=

F ext
2
dt h dt  dK  h dk dt h dk 2
v=
1.5
DENSIDADES DE ELECTRONES Y HUECOS EN SEMICONDUCTORES
Finalidad: calcular la conductividad del semiconductor
N1 de electrones en una banda:
- Densidad de estados por unidad de energía.
- Ocupación de cada estado.
EC
M Densidades de estados:
g n (E) = c n (E -
1
E c )2
g p (E) = c p ( E v - E
1
)2
cn ∝
3
*2
mn
cp ∝
3
* 2
mp
EV
M Función de ocupación de Fermi-Dirac
f(E) =
1
E-EF
1 + e KT
1, E« E F
1
=
, E = EF
2
0, E» E F
M Relación de la posición del nivel de Fermi con la concentración de
electrones y huecos:
EC
EF
EV
½1
f(E)
g(E)
g(E)·f(E)
EC
EF
EV
g(E)·(1-f(E))
½1
g(E)
f(E)
1.6
M Densidad de electrones y huecos
E c max
∫
n=
Ev
p=
g n (E)f(E)dE
Ec
∫
g p (E)(1 - f(E))dE
E v min
! Caso particular: semiconductores no degenerados Ev<EF<Ec
a) En banda de conducción E$Ec>EF
E-EF
e KT
E c max → ∞
∫
n=
>> 1 ⇒ f(E) ≈ e ∞
g n (E)f(E)dE ≈
Ec
E-EF
KT
1
2
∫ c n (E - E c )
e
-
E-EF
KT
dE
Ec
u≡
3
2
n = c n (KT )
Ec - E F
e - KT
∞
E - Ec
KT
1
3
Ec - E F
KT
N c (T) = cte ⋅ T
∫ u 2 e-u du = c n (KT )2 e-
Ec - E F
KT
0
n = N c e-
3
π
2
2
Nc=densidad efectiva de estados en la banda de conducción.
b) En la banda de valencia: E#Ev<EF
e
Ev
p=
∫
E-EF
KT
<< 1 ⇒ f(E) ≈ 1 - e
g p (E)(1 - f(E))dE ≈
E-EF
KT
Ev
1
2
∫ c p( Ev - E )
E-EF
e KT
dE
-∞
E v min
-E
u ≡ Ev
KT
3
2
p = c p (KT )
Ev - E F
e KT
∞
1
∫ u 2 e-u du
0
p=
Ev - E F
N v e KT
N v (T) = cte'⋅ T
EG
np = N c (T) N v (T) e - KT = ni 2
1.7
3
2
(Ley de acción
de masas)
M SEMICONDUCTORES INTRÍNSECOS n=p=ni
E
- G
n i = N c (T) N v (T) e 2KT
Depende del material y de la temperatura
ni(Si,300K).1010cm-3
- Posición del nivel de Fermi:
E c - E Fi
E v - E Fi
n = p ⇒ N c e - KT = N v e KT ⇒
E c + E v + KT ln N v
E Fi =
2
2
Nc
N c = 2.8 ⋅ 10 19 cm- 3
+
En Si, T = 300K : N v = 1.1 ⋅ 10 19 cm - 3 ⇒ E Fi ≈ E c E v - 12meV
2
=
1.12eV
EG
M SEMICONDUCTORES EXTRÍNSECOS: n≠p, n⋅p=ni2
n=p+ND+
! Tipo N:
-Generación de electrones: n=n1+n2
- banda a banda n1=p
- desde impurezas n2=ND+
-Grado de ocupación del nivel creado por las impurezas:
función de ocupación de Fermi-Dirac.
o
1
ND =
N D 1 + e E DKTE F
+
1
ND =
N D 1 + e E FKTE D
-Hipótesis: a temperaturas de interés ND+.ND
en casos prácticos ND>>ni Y n>>p
-Ejemplo: ND=1016cm-3 en Si (((1ppm!!), T=300K
n=p+ND+. ND=1016cm-3
p<<n pero p≠0
Ec-EF=KTln(Nc/n)=205.6meV
Advertencia: a bajas temperaturas ND≠ ND
p=ni2/n=104cm-3
-Ejemplo: Ec-ED=40meV. Calcular temperatura para que ND+= ND/2
1.8
p=n+NA-
! Tipo P:
-Generación de huecos: p=p1+p2
- banda a banda p1=n
- desde impurezas p2=NA-Grado de ocupación del nivel creado por las impurezas:
función de ocupación de Fermi-Dirac.
o
-
1
NA =
N A 1 + e E FKTE A
1
NA =
N A 1 + e E AKTE F
-Hipótesis: a temperaturas de interés NA- ≈ NA>>ni Y p>>n Y
p≈NA
n ≈ ni2/NA
- Advertencia:( COMPROBAR SIEMPRE LAS HIPÓTESIS!
-Ejemplo: NA=1016cm-3 en Si , T=300K, EA-Ev=40meV
p=n+NA- ≈ NA=1016cm-3
n=ni2/p=104cm-3
n<<p pero n≠0
EF-Ev=KTln(Nv/p)=181.4meV
NA-=0.996 NA (99.6%)
EC
EF
EA
EV
!Semiconductores parcialmente compensados:
si N +D > N -A ⇒ tipo N N +D → N +D - N -A
si N +D < N -A ⇒ tipo P N -A → N -A - N +D
Ecuación de neutralidad general:
n + N -A = p + N +D
1.9
CONCENTRACIONES DE PORTADORES DE CARGA EN
DESEQUILIBRIO . GENERACIÓN-RECOMBINACIÓN.
- En desequilibrio no es aplicable el nivel de Fermi.
- Electrones en equilibrio entre sí.
- Huecos en equilibrio entre sí.
- Definición de un nivel de Fermi para cada tipo de partículas y con
carácter local.
n( r ) = N c e -
E c ( r )- E Fn( r )
KT
p( r ) = N v e
E v ( r )- E Fp ( r )
KT
EFn, EFp: pseudoniveles de Fermi.
Situaciones:
np = N c e
np =
E v - E Fp
E Fn - E c
⋅
N v e KT =
KT
qV np
2
n i e KT
E - E E Fn - E Fp
- c v
N c N v e KT e KT
exceso
V np > 0 ⇒ np > ni2
defecto
V np < 0 ⇒ np < n i2
- Agente causante de desequilibrio Y reacción del semiconductor.
exceso Y activación de mecanismos de recombinación.
defecto Y activación de mecanismos de generación.
-)Con qué rapidez responde un semiconductor?
Definición de la probabilidad de generación recombinación.
1.10
Probabilidad de generación recombinación.
N1 de pares electrón hueco que se generan- n1 de pares que se
recombinan por unidad de tiempo.
- U gr ∝ np - n i2 =
exceso:
defecto:
qV np
2
n i ( e KT
np>ni2 Y Ugr<0,
np<ni2 Y Ugr>0,
- 1)
domina recombinación
domina generación
- Caso particular: desequilibrio de bajo nivel
(los mayoritarios apenas se ven afectados)
a) TIPO N:
2
n
i
n ≈ N D , p = p 0 + δp, n0 ⋅ p 0 =
p0 =
ND
np - n i2 = N D ( p 0 + δp) - N D p 0 = N D δ p ⇒
ni2 ,
U gr = b) TIPO P:
δp
τp
2
n
i
p ≈ p 0 = N A , n = n0 + δn, n0 =
NA
np - n i2 = N A ( n0 + δn) - N A n0 = N A δ n ⇒
δn
U gr = τn
- Si se mantiene el agente externo causante de la generación:
U gr = G -
δp
τp
ó U gr = G -
δn
τn
τn,τp: constantes de tiempo de recombinación.
E
EC
- Aumento de la velocidad de
respuesta de los dispositivos
mediante la introducción de
impurezas metálicas que favorecen
la generación-recombinación
absorbiendo momento
(El oro en silicio es la más usada)
EV
000
1.11
k
100
TRANSPORTE DE ELECTRONES Y HUECOS.
CONTRIBUCIONES A LA CORRIENTE.
M Aplicación de un campo eléctrico a un semiconductor
dV(x)
dx
E c (x) = -qV(x) + cte
E(x) = -
-
! Durante un vuelo libre
d
- qE(x) = h k n
dt
EC
EFn
! Interrupciones del vuelo libre
(mecanismos de dispersión):
- vibraciones de la red
- impurezas ionizadas
V
- defectos
- otros portadores, etc
! jn=qnvn vn: velocidad media
de los portadores.
! vn=µnE transporte óhmico
µn:
movilidad de los electrones
(depende de los mecanismos de dispersión, "scattering")
E(x)
! Corriente de arrastre:
E
jn=qnµnE=σnE
jp=qnµpE=σpE
j=jp+jn=(σp+σn)E
M Existencia de un gradiente de concentración de portadores.
Y Flujo de portadores en sentido contrario al gradiente
Y Corrientes de difusión de electrones y de huecos:
(Dn,Dp: coeficientes de difusión)
J n = qD n
M Corriente total
dn
dp
J p = - qD p
dx
dx
dn
dx
dp
J p = qp µ p E - qD p
dx
J = J n+ J p
J n = qn µ n E + qD n
1.12
Relaciones de Einstein:
•


n dE c - dE Fn 
dx 
 dx
dn
n  dV(x) dE Fn 
=- q

dx
KT 
dx
dx 
n = N c e-
E c (x)- E Fn(x)
KT
dn
1
=dx
KT
dV(x) qn
q2
 dV(x) 
dE Fn
+
+ n
J n = qn µ n  Dn
Dn
KT
KT
dx
dx
 dx 
d
En equilibrio E Fn = 0 , J n = 0 ⇒
dx
dV(x) 
q

qn µ n
- µn+
Dn  = 0
dx 
KT

D n = KT
q
µn
se supone válida incluso fuera del equilibrio
J n = µn n
•
dE Fn
dx
dp
1  dV(x) dE Fp 
=
p - q

dx KT 
dx
dx 
D p  dV(x) dE Fp 
 dV(x) 
- q
=
 - pq
J p = qp µ p  KT 
dx
dx 
 dx 
p=
E v (x)- E Fp (x)
N v e KT
= qp
dV
q
p d E Fp
(- µ p +
D p )+ q D p
dx
KT
KT dx
En equilibrio ⇒
D p KT
=
q
µp
en general J p = µ p p
1.13
dE Fp
dx
M Variación de portadores en un elemento de volumen=
Los que entran - los que salen
+ los que se generan - los que se recombinan.
M Análisis unidimensional (por unidad de área):
! Entran por unidad de área y tiempo:
-
x
x+)x
1
J n (x)
q
)x
! Salen por unidad de área y tiempo:
-
1
1
1 ∂Jn
∆x ⇒
J n (x + ∆x) ≈ - J n (x) q
q
q ∂x
 1
∂n
1
1 ∂Jn  
δn 
∆x = - J n (x) -  - J n (x) ∆x  +  G - ∆x
∂t
q
q ∂x
τn
 q
 
∂n 1 ∂ J n
n=
+ G - n0
∂t q ∂x
τn
! De forma similar para huecos:
1
∂p
δp 
1
1 ∂ J p  
∆x = J p (x) -  J p (x) +
∆x  +  G - ∆x
∂t
q
q ∂x
q
  τ p
p - p0
∂p
1∂Jp
=+G ∂t
q ∂x
τp
M Ecuación de Poisson:
d 2 V(x) = - ρ (x)
εs
dx 2
1.14
Caso particular:
E = 0, G = 0 ⇒ J n = q D n
dn
dx
2
∂Jn
n
= q Dn ∂ 2 ⇒
∂x
∂x
2
∂n
n n∂
= D n 2 - n0
∂t
∂x
τn
EJEMPLO:
G
situación estacionaria pero no homogénea:
∂n
∂n
= 0, ≠ 0
∂t
∂x
2 ′
n n′
∂
n′ ≡ n - n0 ⇒ 0 = D n
2
∂x τn
2
2 ∂ n′
≡
⇒
- n′
0
=
Ln
Dnτ n
Ln
2
∂x
x
x
n′(x) = A e - Ln + B e Ln
Si el semiconductor es infinitamente largo
x
n′(x) = A e - Ln
J n = q Dn
En la superficie:
x
∂n
= -qn′(0) D n e - Ln
∂x
Ln
0=G-
n′
τn
n′ = n′(0) = G τ n
1.15