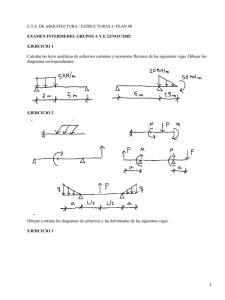
vigas isostaticas vigas - U

CURSO
ESTRUCTURAS I
ELEMENTOS SOMETIDOS A FLEXION
VIGAS ISOSTATICAS
Profesor: Jing Chang Lou
ELEMENTOS SOMETIDOS A FLEXION
VIGAS
La viga es un elemento estructural en forma prismática,
larga y rectas, que están sometido a cargas laterales; es
decir, a fuerzas perpendiculares al eje longitudinal de la
barra causándoles efectos de corte y de flexión.
1
ELEMENTOS SOMETIDOS A FLEXION
VIGAS
TIPO DE VIGAS : VIGAS ISOSTATICAS
ELEMENTOS SOMETIDOS A FLEXION
VIGAS
EJEMPLO
2
ELEMENTOS SOMETIDOS A FLEXION
VIGAS
EJEMPLO
ELEMENTOS SOMETIDOS A FLEXION
VIGAS ISOSTATICAS
FUERZAS CORTANTES Y MOMENTOS FLEXIONANTES
3
ELEMENTOS SOMETIDOS A FLEXION
VIGAS ISOSTATICAS
FUERZAS CORTANTES Y MOMENTOS FLEXIONANTES
ELEMENTOS SOMETIDOS A FLEXION
VIGAS ISOSTATICAS
FUERZAS CORTANTES Y MOMENTOS FLEXIONANTES
∑Fy = 0
V' = R A
V' = P
∑M
X
=0
M' = R A x − M A
M ' = Px − PL
4
ELEMENTOS SOMETIDOS A FLEXION
VIGAS ISOSTATICAS
FUERZAS CORTANTES Y MOMENTOS FLEXIONANTES
∑Fy = 0
V' = R A
V' = P
∑M
X
=0
M' = R A x − M A
M ' = Px − PL
ELEMENTOS SOMETIDOS A FLEXION
VIGAS ISOSTATICAS
FUERZAS CORTANTES Y MOMENTOS FLEXIONANTES
∑Fy = 0
V ' = R A − qx
V ' = qL − qx
∑M
X
=0
M ' = R A x − qx
M ' = qLx −
x
− MA
2
qx 2 qL2
−
2
2
5
ELEMENTOS SOMETIDOS A FLEXION
VIGAS ISOSTATICAS
FUERZAS CORTANTES Y MOMENTOS FLEXIONANTES
∑Fy = 0
V ' = R A − qx
V ' = qL − qx
∑M
X
=0
M ' = R A x − qx
M ' = qLx −
x
− MA
2
qx 2 qL2
−
2
2
ELEMENTOS SOMETIDOS A FLEXION
VIGAS ISOSTATICAS
FUERZAS CORTANTES Y MOMENTOS FLEXIONANTES
∑Fy = 0
x
2
qL qx x
V' =
−
2
L 2
V ' = R A − q'
V' =
∑M
X
qL qx 2
−
2
2L
=0
M ' = R A x − q'
q' =
qx
L
M' =
xx
− MA
23
qL
qx 3 qL2
x−
−
2
6L
3
6
ELEMENTOS SOMETIDOS A FLEXION
VIGAS ISOSTATICAS
FUERZAS CORTANTES Y MOMENTOS FLEXIONANTES
∑Fy = 0
x
2
qL qx x
V' =
−
2
L 2
V ' = R A − q'
qL qx 2
−
2
2L
V' =
∑M
=0
X
M ' = R A x − q'
M' =
xx
− MA
23
qL
qx 3 qL2
x−
−
2
6L
3
ELEMENTOS SOMETIDOS A FLEXION
VIGAS ISOSTATICAS
FUERZAS CORTANTES Y MOMENTOS FLEXIONANTES
∑Fy = 0
V ' = −R A
V' = −
∑M
X
M
L
=0
M ' = −R A x
M' = −
Mx
L
7
ELEMENTOS SOMETIDOS A FLEXION
VIGAS ISOSTATICAS
FUERZAS CORTANTES Y MOMENTOS FLEXIONANTES
∑Fy = 0
V ' = −R A
V' = −
∑M
X
M
L
=0
M ' = −R A x
Mx
L
M' = −
ELEMENTOS SOMETIDOS A FLEXION
VIGAS ISOSTATICAS
FUERZAS CORTANTES Y MOMENTOS FLEXIONANTES
∑Fy = 0
V ' = −R A
V' = −
∑M
X
M
L
=0
M ' = −R A x
M' = −
Mx
L
8
ELEMENTOS SOMETIDOS A FLEXION
VIGAS ISOSTATICAS
FUERZAS CORTANTES Y MOMENTOS FLEXIONANTES
∑Fy = 0
V ' = −R A
V' = −
∑M
M
L
=0
X
M' = −R A x + M
M' = −
Mx
+M
L
ELEMENTOS SOMETIDOS A FLEXION
VIGAS ISOSTATICAS
FUERZAS CORTANTES Y MOMENTOS FLEXIONANTES
∑Fy = 0
V' = −
M
L
TRAMO 1
V' = −
M
L
TRAMO 2
∑M
X
=0
M' = −
Mx
L TRAMO 1
M' = −
Mx
+M
TRAMO 2
L
9
ELEMENTOS SOMETIDOS A FLEXION
VIGAS ISOSTATICAS
FUERZAS CORTANTES Y MOMENTOS FLEXIONANTES
ELEMENTOS SOMETIDOS A FLEXION
VIGAS ISOSTATICAS
FUERZAS CORTANTES Y MOMENTOS FLEXIONANTES
10
ELEMENTOS SOMETIDOS A FLEXION
VIGAS ISOSTATICAS
FUERZAS CORTANTES Y MOMENTOS FLEXIONANTES
ELEMENTOS SOMETIDOS A FLEXION
VIGAS ISOSTATICAS
FUERZAS CORTANTES Y MOMENTOS FLEXIONANTES
11
ELEMENTOS SOMETIDOS A FLEXION
VIGAS ISOSTATICAS
FUERZAS CORTANTES Y MOMENTOS FLEXIONANTES
BIBLIOGRAFIA
DISEÑO Y CALCULO DE ESTRUCTURAS
•Bernardo Villasuso (1994) – El Ateneo – Buenos Aires - Argentina.
MECANICA VECTORIAL PARA INGENIEROS - ESTATICA
Ferdinand P. Beer, E. Russell Johnston Jr (1990) – Ediciones
McGraw-Hill.
DISEÑO ESTRUCTURAL
Rafael Riddell C., Pedro Hidalgo O. (2002) 3°Ed. Ediciones PUC de
Chile.
FUNDAMENTOS DE INGENIERIA ESTRUCTURAL PARA
ESTUDIANTES DE ARQUITECTURA
Rafael Riddell C., Pedro Hidalgo O. (2000) Ediciones PUC de Chile.
12