Guía de Problemas. Hidrostática. 1. Un tanque cerrado está

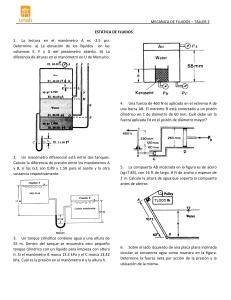
Guía de Problemas. Hidrostática.
1. Un tanque cerrado está parcialmente lleno con glicerina. Si la presión del aire
dentro del tanque es de 6 psi (41,37 kPa) y el nivel de glicerina es de 10 ft
(3,05 m), cual será la presión en el fondo del tanque?.( γglicerina = 12,4 kN/m3)
2. Se tiene un tanque construido por una serie de cilindros con los siguientes
diámetros : 0,3 ; 0,25 y 0,15 m como se muestra en la figura. El tanque contiene:
aceite (γaceite = 8,95 kN/m3), agua (γagua = 10 kN/m3) y glicerina (γglicerina = 12,4
kN/m3) y en el fondo del mismo se coloca un manómetro de mercurio. Se pide
calcular la altura h indicada por el manómetro.
3. Determine la inclinación del tubo del manómetro si para las condiciones
mostradas en la figura la presión en A supera a la presión en B por 6,89 kPa.
(Nota: SG es la densidad del líquido relativa a la del agua, es decir SG = ρ/ ρagua)
4. Una piscina tiene 7 m de ancho y 18 m de largo. Determinar la magnitud y la
ubicación de la fuerza horizontal que experimenta cada una de las paredes
laterales de la piscina. Considerar que la profundidad de la misma es constante e
igual a 2,5 m.
5. La figura muestra la sección transversal de un tanque cerrado de 7 m de largo. El
tanque contiene alcohol etílico y la presión del aire es de 40 kPa. Determine la
magnitud de la fuerza resultante que actúa sobre la base del tanque.
6. Un tanque abierto tiene en una de sus paredes laterales una compuerta triangular
como la mostrada en la figura. La puerta puede pivotar respecto al eje A-B.
Conociendo las dimensiones del tanque y que este contiene agua se pide:
determinar el momento, respecto al eje A-B, que es necesario aplicar para
mantener la compuerta cerrada.
7. La compuerta rectangular C-D de la figura tiene 2 m de ancho y 1,8 m de largo.
Asumiendo que el material de la compuerta es homogéneo y despreciando la
fricción en la bisagra C, se pide: determinar el peso de la compuerta de manera
que esta permanezca cerrada hasta que el nivel del agua esté 2 m por encima de
la bisagra.
8. Una compuerta con la forma de una superficie cilíndrica parcial (conocida como
compuerta Tainter) es empleada para contener el agua en un dique como
muestra la figura. El radio de la superficie es de 6,7 m y su longitud es de 11 m.
La compuerta puede pivotar respecto del punto A y a su vez dicho punto está 3
m por encima del punto de apoyo de la compuerta (C). Determine la magnitud
de la fuerza resultante sobre la compuerta. ¿Pasará esta resultante por el punto
A?, justifique.
9. Un tapón cónico es colocado en la pared de un tanque como se muestra en la
figura. Mostrar que la fuerza horizontal que el agua ejerce sobre el tapón no
depende de h. Para la profundidad indicada: ¿cuál será la magnitud de dicha
fuerza? (Nota: 1ft = 0,3048 m)
10. El cilindro de la figura (de 2,74 m de longitud) se mantiene flotando en aceite y
en contacto con la pared. Se pide: determinar la fuerza horizontal que el cilindro
ejerce sobre la pared en el punto A. (Nota: γaceite = 9,13 kN/m3 )
11. Un globo aerostático pesa 225 kg incluyendo el peso del globo, la canasta y un
pasajero. El aire ambiente tiene una temperatura de 26 ºC mientras que el aire
caliente contenido en el globo está a 66 ºC. Asumiendo que tanto el aire
ambiente como el contenido en el globo tiene una presión estándar de 100 kPa
(1 atm), se pide: determinar el volumen del globo para soportar el peso total.
Asumiendo un globo esférico establecer el radio del mismo. (Nota: considerar
al aire como un gas ideal. p = ρ.R.T)
12. Una pieza de forma irregular pesa 3,65 kg en aire y 2,39 kg cuando está
completamente sumergido en agua. Determinar la densidad del objeto.
13. Un cubo de 1,2 m de arista y 1360 kg de peso flota sumergido hasta la mitad en
un líquido contenido en un tanque abierto como se observa en la figura. Se pide
determinar la magnitud, dirección y ubicación de la fuerza ejercida por el líquido
sobre la superficie inclinada A-B. El ancho del tanque es de 2,44 m.
14. Un recipiente que está parcialmente lleno con agua es acelerado en forma
uniforme según la dirección horizontal. Debido a la aceleración la superficie
libre del líquido forma un ángulo de 40º respecto de la dirección de la
aceleración como muestra la figura. Determinar el valor de la aceleración
aplicada.
15. Un recipiente cilíndrico de 0,6 m de diámetro esta parcialmente lleno con agua.
El nivel de agua alcanza 1 m cuando el recipiente está en reposo. Si el tanque
comienza a ser rotado respecto de su eje vertical a una velocidad angular
constante (ω = 160 rev/min) determinar la altura mínima que tiene que tener el
cilindro para evitar que se derrame su contenido.
16. Un acelerómetro barato puede hacerse con un tubo en U como indica la figura.
Las variaciones de nivel h son dan una medida del valor de la aceleración según
el eje x. Para L = 0,2 m y D = 0,01 m determinar el valor de h cuando la
aceleración según el eje x es constante e igual a 5 m/s2?
17. Una pieza con simetría axial es manufacturada por moldeado centrífugo como
indica la figura. Durante el proceso de conformado el molde de arena rota con
una velocidad angular constante (Ω). Se pide:
a) Calcular la presión p1 en [1] en función de Ω.
b) Determinar la velocidad angular máxima (Ωmáx) tal que en [1] no se supere
la presión máxima tolerada por el molde (pmáx)
c) Calcular para la velocidad angular hallada en el punto anterior (Ωmáx) la
altura h máxima tal que en el punto [2] la presión no supere el valor de pmáx
18. La noria de la figura de 2 m de radio es utilizada para elevar agua por medio de
sus poleas semicilíndricas de 0,3 m de diámetro. Si la noria gira a 10 r.p.m. y
suponemos movimiento como sólido rígido: ¿cuál es el ángulo θ que forma la
superficie libre con la horizontal en la posición A de su trayectoria circular?