cm % de volumen. Una hormiga camina desde el punto A hasta el

1. El cubo de la …gura tiene 27cm3 de volumen. Una hormiga camina desde
el punto A hasta el punto B siguiendo la ruta que se muestra en la …gura.
¿Cuántos centímetros recorrió la hormiga?
(a)9
(b)10
(c)12
(d)15
(e)No se puede determinar
Solución:
La hormiga recorrió una distancia igual a 5 veces la longitud de cada
arista. Como el volumen del cubo es de 27cm3 , cada arista mide 3cm, por
lo tanto la hormiga recorrió 5 3 = 15cm.
Respuesta correcta: (d)
2. Mario es mayor que Zelda por 128 días, este año Mario celebró su cumpleaños
en martes, ¿En qué día celebrará su cumpleaños Zelda?
(a)martes (b)miércoles (c)jueves (d)viernes
(e)domingo
Solución:
Mario es mayor que Zelda por 18 semanas y dos días, así que el cumpleaños
de Zelda será dos días después de un martes, o sea, un jueves.
Respuesta correcta:(c)
3. Si xy + 5 = 4x, ¿Cuánto vale y + x5 ?
(a)5
(b)0
(c)20
(d)4
(e)No se puede determinar
Solución:
Tenemos que y + x5 = xyx+5 , luego dividiendo entre x la igualdad inicial
tenemos xy+5
= 4, por lo tanto y + x5 = 4:
x
Respuesta correcta:(d)
4. En la ecuación a + 3b = 2001, a y b son enteros. ¿Cuál de los siguientes
valores es imposible para a ?
(a)3
(b)45
(c)111
(d)1001
(e)2001
Solución:
Como 2001 y 3b son múltiplos de 3, a también debe ser un múltiplo de 3.
El único número que no lo es, es 1001. En los demás casos, a es múltiplo
de 3 y podemos tomar b = 20013 a , que es un entero.
Respuesta correcta: (d)
1
5. Julio pegó 7 dados de manera que coincidieran los números de las caras
pegadas. ¿Cuántos puntos quedaron en total en la super…cie?
(a)95
(b)102
(c)105
(d)112
(e)126
Solución:
Considerando los 6 dados exteriores antes de pegarlos, el total de puntos
en sus super…cies es 6(1 + 2 + 3 + 4 + 5 + 6) = 126. A esta cantidad hay
que restarle la suma de los puntos en la super…cie del dado que quedará
al centro (cada uno de los lados de afuera se pega por el mismo número al
dado central), que es 1 + 2 + 3 + 4 + 5 + 6 = 21: Así, la cantidad de puntos
que quedaron en la super…cie es 126 21 = 105:
Respuestas correcta: (c)
6. Lucero y David van al cine y entran en una sala que tiene 12 …las de 13
asientos cada una, observan que varios asientos ya se han ocupado, ¿Cuál
es el máximo número de asientos ocupados que puede haber para asegurar
que Lucero y David se pueden sentar juntos en la misma …la?
(a)71
(b)83
(c)154
(d)72
(e)78
Solución:
Tenemos que tomar el peor de los casos, es decir el caso en el que Lucero
y David no se puedan sentar juntos en alguna …la, es fácil ver qué ocurre
cuando alternadamente hay asientos ocupados y desocupados, si a cada
asiento de una …la le asignamos un número en orden 1, 2, 3, ..., 13, y
están ocupados todos los asientos impares, tendríamos 7 lugares ocupados,
mientras que si ocupamos todos los asientos pares tendríamos 6 lugares
ocupados. Entonces en el peor de los casos en cada …la estarían ocupados
todos los asientos pares por lo que tendría que haber 6 personas por …la
6 12 = 72: Por lo tanto con solo 71 personas aseguramos que Lucero y
David se podrán sentar juntos.
Respuesta correcta: (a)
7. Si cortamos un rectángulo por la mitad y ponemos una pieza encima de
la otra obtenemos un cuadrado cuya área es 144cm2 :¿Cuál es el perímetro
del rectángulo con el que empezamos?
2
(a)24cm
(b)30cm
(c)48cm
(d)60cm
(e)72cm
Solución:
Si el área del cuadrado es 144cm2 entonces sus lados miden 12cm. Es
fácil ver que dividimos el rectángulo grande en dos rectángulos pequeños
iguales, el largo de estos es igual al lado del cuadrado, es decir 12cm:Por
otra parte el ancho de los rectángulos pequeños mide la mitad del lado
del cuadrado, es decir 6cm; por lo tanto el perímetro del rectángulo con
el que empezamos es 12cm + 12cm + 12cm + 12cm + 6cm + 6cm = 60cm
Respuesta correcta: (d)
8. En el triángulo ABC de la …gura el segmento BH es una altura y los
ángulos \CAD y \DAB miden lo mismo, el ángulo mayor entre AD y
BH mide 4 veces lo que el \DAB, así como se ha marcado en la …gura.
¿Cuál es la medida del ángulo \CAB?
(a)30o
(b)45o
(c)60o
(d)75o
(e)90o
Solución
Por la sumatoria de los ángulos internos de un triángulo tenemos que
+ 90 + (180
4 ) = 180; + 90 = 4 ; 3 = 90 ; = 30 ; luego
\CAB = 2 = 60 :
Respuesta correcta: (c)
9. En un curso se aplican 5 examenes. Todos tienen la misma puntuación
máxima, pero la cali…cación …nal se obtiene como sigue: la cali…cación del
primer examen se promedia con la del segundo; el resultado se promedia
con la cali…cación del tercero; el resultado se promedia con la cali…cación
del cuarto examen y, …nalmente, el resultado se promedia con la quinta
cali…cación. ¿En qué porcentaje de la cali…cación …nal contribuye el tercer
examen?
3
(a)10%
(b)12:5%
(c)20%
(d)25%
(e)Depende de las cali…caciones
Solución:
Haciendo el primer promedio:
1o +2o
2 o ;el
o
segundo:
1 +2 +3o
2
+4o
2
2
1o +2o
2
+3o
2
;el tercero:
1o +2o +3o
2
2
+5o
…nalmente el cuarto promedio:
:Notemos que en el último
2
promedio el 5o examen equivale al 50% de la cali…cación …nal mientras que
1o +2o +3o
2
2
+4o
2
también es el 50%, de esto sale que el 4o examen vale pues
1o +2o
+3o
también vale 25%, de igual forma se obtiene
el 25% por lo que 2 2
que el 3o equivale al 12:5% de la cali…cación …nal.
Respuesta correcta (b)
10. ¿Cuál es la suma de los dígitos de 111:::11
| {z } 101?
2014
(a)2012
(b)2016
(c)4028
(d)4032
(e)8056
Solución
Tenemos que:
|111:::11
{z } 101 = 111:::11
| {z } (100 + 1) = |111:::11
{z } 00 + |111:::11
{z } = 11 222:::22
| {z } 11
2014
2014
2014
2014
2012
luego la suma de los dígitos es
2 2012 + 4 = 4028:
Respuesta correcta: (c)
11. En un rectángulo de 6 11 se trazan las rectas que dividen a la mitad cada
uno de los ángulos que están en los extremos de uno de los lados que mide
11, de forma que el lado opuesto queda dividido en tres partes.¿Cuáles son
las longitudes de esas tres partes?
(a)5; 1; 5
(b)2; 7; 2
(c)3; 5; 3
Solución:
4
(d)4; 3; 4
(e)1; 9; 1
2
+4o
;y
La …gura queda de la siguiente forma:
Como AF es bisectriz de \DAB que mide 90 , entonces \DAF = 45 ;
por la sumatoria de los ángulos interiores de un triángulo tenemos que
\DAF +\ADF +\DF A = 180; 45 +90 +\DF A = 180 ; \DF A = 45 .
Como \DAF = \DF A = 45 entonces 4ADF es un triángulo isósceles
con AD = DF = 6:Análogamente podemos llegar a que BC = CE = 6.
Finalmente tenemos que DC = CE + DE; 11 = 6 + DE; DE = 5,
análogamente F C = 5, luego CE = EF + F C; 6 = EF + 5; EF = 1, así
que las longitudes de las tres partes son 5; 1; 5:
Respuesta correcta: (a)
12. Se tiene una baraja que consta de cartas de varios colores distintos, en
la baraja hay 5 cartas de cada color. Se reparten todas las cartas de la
baraja entre 4 personas, ¿Cuál es la probabilidad de que al menos a una
persona le toquen a lo menos 2 cartas del mismo color?
(a)1
(b) 45
5
(c) 11
(d) 25
(e)No se puede determinar
Solución:
Como hay 5 cartas de un mismo color y se van a repartir todas a 4 personas,
entonces al menos a una persona siempre le tocarán a lo menos dos cartas
del mismo color (principio de las casillas), por lo tanto la probabilidad es
1.
Respuesta correcta: (a )
13. En la siguiente …gura se tiene que CE = DE, además ]CAB = 50o y
]BDE = 25o .¿Cuánto mide ]CED?
5
(a)80o
(b)50o
(c)45o
(d)30o
(e)No se puede determinar.
Solución:
Tenemos que ]CAB es un ángulo central y que ]CDB es una ángulo
=
inscrito en el mismo arco que ]CAB, por lo tanto ]CDB = ]CAB
2
50o
o
o
=
25
;
luego
]CDE
=
50
:
Como
CE
=
DE
entonces
4CDE
es
2
isósceles con ]CDE = ]DCE = 50o . Finalmente por la sumatoria de los
ángulos internos de un triángulo tenemos que ]CDE +]DCE +]CED =
180o ; es decir 50o + 50o + ]CED = 180o ; luego ]CED = 80o :
Respuesta correcta: (a)
14. Si 4x = 9 y 9y = 256, ¿A qué es igual xy?
(a)2006
(b)48
(c)36
(d)10
(e)4
Solución:
Como (4x )y = 4xy = 9y = 256 = 44 , tenemos que xy = 4.
Respuesta correcta: (e)
15. Se lanzan dos dados distintos uno azul y otro rojo. ¿Cuál es la probabilidad
de que la suma de las caras que quedan hacia arriba sea un número primo?
36
(a) 36
5
(b) 36
5
(c) 11
5
(d) 15
5
(e) 12
(Un número primo es aquel que tiene únicamente dos divisores positivos)
Solución:
Los números primos que podemos obtener como suma son 2; 3; 5; 7 y 11,
y las formas distintas de obtener cada número primo son 1; 2; 4; 6 y 2
respectivamente.
Como los dados son distintos, no es lo mismo 1 + 3 que 3 + 1, observemos
que las formas de obtener por ejemplo 5 son 1 + 4; 2 + 3; 3 + 2; 4 + 1; es
decir 4 formas.
Así que el total de formas en las que obtenemos como suma un número
primo son 1 + 2 + 4 + 6 + 2 = 15, y como el total de resultados al lanzar
5
15
= 12
los dados es 6 6 = 36 entonces la probabilidad es 36
Respuesta correcta: (e)
6
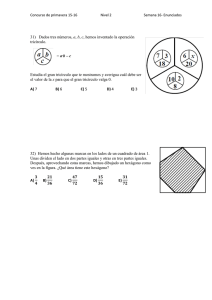
16. Recordando que las tarántulas y los ratones tienen 8 y 4 patas respectivamente, si en un conjunto de tarántulas y ratones el cuádruple del número
de cabezas más 12 es igual al número de patas en el conjunto. ¿Cuántas
tarántulas hay en el conjunto?
(a) 3 (b) 12 (c) 1 (d) no se puede determinar (e) ninguno de los anteriores
Solución:
Los ratones tienen 4 patas y una cabeza, las tarántulas tienen 8 patas y una
cabeza por lo tanto podemos plantear la siguiente ecuación: 4(x+y)+12 =
8x + 4y, donde "x" es el número de tarántulas y "y" el número de ratones.
Luego de la ecuación:
4x + 4y + 12 = 8x + 4y; 12 = 4x; x = 3
Por lo tanto hay 3 tarántulas en el conjunto.
Respuesta correcta: (a)
17. En la …gura se muestran dos hexágonos regulares. Los lados del hexágono
grande miden el doble que los del hexágono pequeño. El hexágono pequeño
tiene un área de 4cm2 : ¿Cuál es el área del hexágono grande?
(a)24cm2
(e)12cm2
(b)18cm2
(c)16cm2
(d)15cm2
Solución:
Sean P y A el perímetro y el apotema del hexágono grande, y sean p y
a el perímetro y el apotema del hexágono pequeño respectivamente. El
área del hexágono pequeño es 4cm2 = p2a : Como los lados del hexágono
grande son el doble de los lados del pequeño entonces P = 2p; además
A = 2a: Luego el área S del hexágono grande es S = P 2A = 2p22a =
4p a
2
2
2 = 4 4cm = 16cm .
Respuesta correcta: (c)
18. ¿Cuántos números de 5 dígitos abcde existen tales que a + b, b + c, c + d
y d + e son todos números pares?
(a)55
(b)54
(c)2 55
(d)54 9
(e)Otra respuesta
Solución:
Los números que cumplen esto son los que tienen todos sus dígitos pares o
todos sus dígitos impares. Si contamos primero los que tienen sus dígitos
impares hay que tomar en cuenta que tenemos cinco dígitos impares, 1,
3, 5, 7 y 9, por principio fundamental del conteo tenemos que a tiene 5
7
valores posibles e igualmente b, c, d y e, por lo que el total de números
que hay en este caso es 5 5 5 5 5 = 55 :Análogamente en el caso donde
todos los dígitos son pares hay 4 5 5 5 5 = 4 54 (ya que los dígitos
posibles son 0, 2, 4, 6 y 8, solo que en a no puede valer cero, entonces el
conteo cambia a 4 5 5 5 5 = 4 54 )
Luego 55 + 4 54 = 54 (5 + 4) = 54 9. Por lo tanto el resultado es 54 9:
Respuesta correcta: (d)
19. Cada uno de los lados del cuadrado que se muestra en la …gura mide 24
cm. En su interior se dibujaron 5 rectángulos iguales.¿Cuál es el área de
cada uno de esos rectángulos?
(a)32cm2
(e)12cm2
(b)24cm2
(c)18cm2
(d)16cm2
Sea "x" y "y" el largo y ancho de los rectángulos respectivamente, expresando el lado del cuadrado en términos de "x" y "y" es fácil ver que
x + (x y) + y + x = 24; 3x = 24; x = 8. Por otra parte también tenemos
que y + x + x + y = 24; como x = 8 entonces 2y = 24 16, y = 4 luego
el área de los rectángulos es 4 8 = 32
Respuesta correcta: (a)
20. Varios piratas se repartieron un cofre con monedas de oro de manera que
cada uno le tocó la misma cantidad. Si hubiera habido cuatro piratas
menos, a cada persona le habría tocado 10 monedas más. Si hubiera
habido 50 monedas menos, a cada persona le hubieran tocado 5 monedas
menos que en el reparto original. ¿Cuántas monedas se repartieron en
total?
(a)80
(b)100
(c)120
(d)150
(e)250
Solución:
Sea "x" la cantidad original de piratas y sea "y" la cantidad de monedas
que le tocaron a cada pirata en el reparto original, observemos entonces
que "xy" es el total de monedas que se repartieron en total. Si hubiera
habido cuatro piratas menos, a cada persona le habría tocado 10 monedas
más, es decir:
8
(x
4)(y + 10) = xy; xy + 10x
4y
40 = xy; 10x
4y = 40
Si hubiera habido 50 monedas menos, a cada persona le hubieran tocado
5 monedas menos que en el reparto original, es decir:
x(y
5) = xy
50; xy
5x = xy
50;
5x = 50; x = 10
Por lo tanto originalmente había 10 piratas, luego sustituyendo en 10x
4y = 40; 100 4y = 40; 4y = 60; y = 15; luego a cada pirata le tocaron 15
monedas en el reparto original, por lo tanto había 15 10 = 150 monedas.
Respuesta correcta: (d)
21. Todos los ángulos interiores de un polígono convexo son menores que 108o .
El número de lados de ese polígono puede ser a lo más:
(a)3
(b)4
(c)5
(d)6
(e)7
(Un polígono convexo es aquel que tiene todos sus ángulos menores que
180o )
Solución:
Observemos que si n es el número de lados de un polígono convexo, entonces la suma de sus ángulos interiores está dada por 180(n 2):Como
todos los ángulos son menores que 108o , tenemos que 180(n 2) < 108n,
luego 72n < 360, de donde n < 5. Por lo tanto, a lo más el polígono puede
tener 4 lados.
Respuesta correcta: (b)
22. Al …nal de un día de ventas, Mariana y Ricardo juntaron el dinero que
ganó cada uno y se lo repartieron en partes iguales. Haciendo esto, Ricardo perdió un 30% del dinero que había ganado. ¿Qué porcentaje ganó
Mariana?
(a)20%
(b)25%
(c)30%
(d)70%
(e)75%
Solución:
Tomemos lo que Mariana vendió como un porcentaje de lo que Ricardo
vendió, Ricardo perdió 30% por lo que le queda sólo 70% de lo que ganó,
como se repartieron equitativamente la ganancias entonces Mariana al
…nal también quedo con un 70% de lo que ganó Ricardo. Por tanto como
Mariana recibió 30% de lo que Ricardo vendió, entonces ella solo vendió
40% de lo que Ricardo. Finalmente es fácil notar que 30% son 43 de 40%,
por lo que Mariana recibe un aumento del 75% de lo que vendió.
Respuesta correcta: (e)
23. Una caja tiene 900 tarjetas numeradas del 100 al 999 (una con cada
número). Francisco va a extraer de la caja algunas de las tarjetas y apuntará la suma de los dígitos de cada una (por ejemplo, si toma las tarjetas
209,833 y 911, apuntará 11, 14 y 11). ¿Cuántas tarjetas debe tomar para
poder garantizar que tomará tres cartas al menos con la misma suma de
dígitos?
9
(a)51
(b)52
(c)53
(d)54
(e)55
Solución:
Las posibles sumas de los dígitos son los números del 1 al 27; la suma 1 sólo
se logra con el número 100, y la suma 27 sólo se logra con el número 999.
Todas las demás sumas se logran con al menos dos números. Entonces
sería posible que Francisco escogiera el 100, el999 y dos números de cada
una de las otras 25 sumas y todavía no habría encontrado 3 números con
la misma suma de dígitos; una tarjeta extra forzosamente repetiría suma.
Respuesta correcta: (c)
24. En la …gura se tiene que ]BAE = ]ADE, si ]ACE = 30o y ]DAE =
25o ;¿Cuánto mide ]BAD + ]EAC ?
(a)90o
(b)100o
(c)60o
(d)77:5o
(e)50o
Solución:
Por la sumatoria de los ángulos internos de un triángulo tenemos que
]DAE + ]CAE + ]ACE + ]ADE = 180o , es decir 25o + ]CAE + 30o +
]ADE = 180 , por lo tanto ]EAC + ]ADE = 125o y como ]BAE =
]ADE, entonces ]EAC+]BAE = 125o :Por otra parte ]BAE = ]DAE+
]BAD; luego ]EAC + ]DAE + ]BAD = 125o , pero como ]DAE =
25o ;llegamos a que ]EAC+25o +]BAD = 125o y ]EAC+]BAD = 100o
Respuesta correcta: (b)
25. Dos lados de un triángulo acutángulo y la altura sobre el tercer lado tienen
longitudes 12,13 y 15 (tal vez no en ese orden). ¿Cuál es el área del
triángulo?
(a)168
saber
(b)156
(c)80
Solución:
10
(d)84
(e)no se puede
La altura debe tener la longitud más corta, 12. Entonces tenemos el
triángulo de la siguiente forma:
Luego por teorema de Pitágoras BH = 9 y HC = 5, entonces BC = 14 y
el área del triángulo es BC 2AH = 12214 = 84:
Respuesta correcta: (d)
26. María y Luisa compitieron resolviendo una lista de 100 problemas. Algunos problemas no fueron por ninguna pero otros los resolvieron las dos.
Por cada problema resuelto, la primera en resolverlo obtuvo 4 puntos y, en
caso que lo hubieran resuelto las dos, la segunda obtuvo sólo un punto. Si
cada una de ellas resolvió 60 problemas de la lista y entre las dos lograron
312 puntos, ¿cuántos problemas resolvieron en común?
(a)57
(b)56
(c)55
(d)54
(e)53
Solución:
Sea k la cantidad de problemas que resolvieron en común, observemos que
María resolvió 60 k = a problemas que Luisa no pudo resolver, pero
también Luisa resolvió 60 k = a problemas que María no pudo resolver.
Por cada uno de los k problemas que resolvieron las dos, acumulan 5
puntos, ya que una acumula 4 puntos y la otra 1 punto. Además por cada
uno de los a problemas que María resolvió y Luisa no, María acumula 4
puntos. Pero también por cada uno de los a problemas que Luisa resolvió
y María no, Luisa acumula 4 puntos. Como entre las dos tuvieron una
puntuación de 312; podemos plantear la ecuación: 4a+4a+5k = 312. Pero
además ya teníamos que a + k = 60. Resolviendo el sistema de ecuaciones
tenemos que a = 4 y k = 56, por lo tanto la cantidad de problemas que
resolvieron en común son 56:
Respuesta correcta:(b)
27. En la siguiente …gura CD =
p
p
18, EC = 3, ED = 3; AC = 9 2, CB = 9;
11
¿Cuál es la medida de ]CAB ?
(a)30o
(b)45o
se puede determinar
(c)55o
(d)60o
(e)no
Solución:
Observemos que el CED es un triángulo rectángulo con hipotenusa CD
ya que se cumple el teorema de Pitágoras.
p
p
p
32 + 32 = 9 + 9 = 18
Pero además el CED es isósceles ya que EC = ED = 3 y por lo tanto
\ECD = \EDC, por la sumatoria de los ángulos internos de un triángulo
o
o
o
\EDC = 180 2\CED = 180 2 90 = 45o
Por otra parte
p
p 18
3 32 2
=
ABC:
p
18
p
9 2
CED
=
EC
CB
=
ABC por criterio LAL ya que
CD
AC
3
9
y el ángulo \ACB es común de
=
p
p18
3 18
=
CED y
De la semejanza se tiene que \EDC = \CAB = 45o
Respuesta correcta: (b)
28. En la siguiente …gura, ¿Cuantos caminos distintos hay para ir del punto
A al punto B, si solo se puede avanzar en las direcciones: &, #, % ; ! ?
12
(a)71
(b)83
(c)55
(d)53
(e)78
Solución:
Contamos las formas en que podemos llegar a los puntos más próximos a
"A", a cada punto podemos llegar por las direcciones opuestas a las que
podemos avanzar. Por ejemplo las formas en que podemos llegar a "G"
son llegar desde los puntos A, F y H, como solo podemos llegar de 1 forma
a cada uno, entonces el total de caminos hasta G son 1 + 1 + 1 = 3.
Siguiendo el mismo procedimiento podemos saber cuántos caminos hay
hasta "K", como podemos llegar desde "A"; "I"; "G" y "H" entonces los
caminos hasta "K" son: 1 + 2 + 3 + 1 = 7:
Siguiendo el mismo procedimiento obtenemos el total de caminos desde
"A" hasta "B", que son 55:
13
Respuesta correcta: (c)
29. En el bosque hay 20 duendes. Algunos son verdes, otros son amarillos y
otros son morados. Se les hicieron 3 preguntas. Los verdes siempre dijeron
la verdad, los morados siempre mintieron, y cada uno de los amarillos eligió
entre mentir y decir la verdad al responder la primera pregunta y, a partir
de ahí alternó entre verdad y mentira. La primera pregunta que se le hizo
a cada uno fue ¿Eres verde?, a lo que 17 de ellos respondieron "Si". La
segunda pregunta fue ¿Eres amarillo? a lo que 12 de ellos respondieron
"Si". La tercera pregunta fue ¿Eres morado? a lo que 8 respondieron "Si"
¿Cuántos duendes son amarillos?
a)7
(b)8
(c)9
(d)10
(e)11
Solución:
Los duendes verdes y morados no respondieron "Si" a la tercera pregunta,
ya que iría en contra de su naturaleza de siempre decir la verdad y siempre
mentir respectivamente. Por lo tanto todos los duendes que respondieron
"Si" a la tercera pregunta son duendes amarillos que empezaron mintiendo,
es decir 8.
Por otra parte los duendes que empezaron respondiendo la verdad no respondieron "Si" a la primera pregunta y además es claro que el resto (duendes morados, verdes y amarillos que empezaron mintiendo) respondieron
"Si". Por lo tanto los duendes que empezaron respondiendo la verdad son
20 17 = 3.
Luego el total de duendes amarillos son 8 + 3 = 11
Respuesta correcta:(b)
30. Los vértices de un cubo se numeran del 1 al 8 de manera que el resultado
de sumar los cuatro números de cada cara es el mismo para todas las caras.
Se han colocado ya los números 1; 4 y 6 como se muestra en la …gura.¿Qué
número va en el vértice marcado con x?
a)2
(b)3
(c)5
(d)7
Solución:
14
(e)8
Sea S la suma en cada cara y de…namos los vertices del cubo como se
sigue:
Como cada vértice es parte de 3 caras, podemos plantear la siguiente
ecuación:
6S = 3b + 3c + 3a + 3d + 3x + 3 6 + 3 4 + 3 1
2S = b + c + a + d + x + 11 = 1 + 2 + 3 + ::: + 8 = 36
S = 18
Luego observemos que 6 + 1 + 4 + d = S = 18, y d = 7:
Por otra parte 4 + d + c + x = S; 11 + c + x = 18; c + x = 7:
Análogamente a + x = 5:
Entonces:
c + x = 7; a + x = 5
c
a=2
Luego los números que nos faltan por acomodar son, 2; 3; 5 y 8; y los únicos
cuya diferencia es 2 son 5 y 3, luego c = 5 y a = 3
Finalmente c + x = 7; 5 + x = 7; luego x = 2:
Respuesta correcta:(a)
15