PDF

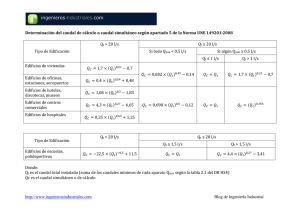
VI SEREA - Seminário Iberoamericano sobre Sistemas de Abastecimento Urbano de Água
João Pessoa (Brasil), 5 a 7 de junho de 2006
APLICACIÓN DE LOS MÉTODOS PARA EL CÁLCULO DE CAUDALES MÁXIMOS
PROBABLES INSTANTÁNEOS, EN EDIFICACIONES DE DIFERENTE TIPO
Nelson Yovani Castro Ladino1,Jorge Enrique Garzón Garzón2,Rafael Orlando Ortiz Mosquera3
Resumen: En complemento de las políticas gubernamentales sobre el uso racional del agua y
continuando las investigaciones desarrolladas por diferentes instituciones, en particular los estudios
que ha realizado la Facultad de Ingeniería de la Universidad Nacional de Colombia a través del
Grupo de Investigación en Ingeniería de Recursos Hídricos (GIREH); ésta investigación recopila,
analiza y evalúa algunos métodos para la estimación de los caudales máximos probables, que
permiten diseñar las redes de suministro de agua en edificaciones. Se exponen siete (7) métodos y
se aplican 6 de éstos a ocho (8) edificaciones de las cuales se conoce el caudal máximo demandado,
como resultado de los aforos realizados en dos (2) trabajos de grado; buscando establecer una
metodología que permita estimar con mayor certeza los consumos reales, para racionalizar el agua,
disminuir costos y hacer más eficientes las instalaciones hidráulicas y los equipos de bombeo donde
sea necesaria su implementación.
ABSTRACT: In complement of the government politicians on the rational use of the water and the
investigations developed by different institutions continuing, in particular the studies that she has
carried out the Ability of Engineering of the National University of Colombia through the Group of
Investigation in Engineering of Resources Hidrics (GIREH); this investigation gathers, it analyzes
and it evaluates some methods for the estimate of the probable maximum flows that they allow to
design the nets of supply of water in constructions. Seven are exposed (7) methods and 6 of these
are applied at eight (8) constructions of which the demanded maximum flow is known, as a result of
the seating carried out in two (2) grade works; looking for to establish a methodology that allows to
estimate with more certainty the real consumptions, to rationalize the water, to diminish costs and to
make more efficient the hydraulic facilities and the teams of pumping where it is necessary their
implementation.
Palabras claves: Métodos de diseño, caudal de diseño y suministro
1
Universidad Nacional de Colombia - Ingeniero Civil – Departamento de Ingeniería civil y Agrícola –Unidad de
Hidráulica –Bogota, Colombia. E-mail: [email protected]
2
Universidad Nacional de Colombia - Ingeniero Civil – Departamento de Ingeniería civil y Agrícola –Unidad de
Hidráulica –Bogota, Colombia. E-mail: [email protected]
3
Universidad Nacional de Colombia - Ingeniero Civil – Departamento de Ingeniería Civil y Agrícola –Unidad de
Hidráulica – M. Sc. En Docencia – Candidato a M. Sc. en Recursos Hidráulicos – Director de la Unidad de Hidráulica Integrante GIREH ( Grupo de investigación de Recursos Hídricos) - Bogota, Colombia. Tel: (+57) 1 3165000 Ext.
13474 – Fax: (+57) 1 3165563 E-mail: [email protected]
VI SEREA - Seminário Iberoamericano sobre Sistemas de Abastecimento Urbano de Água
João Pessoa (Brasil), 5 a 7 de junho de 2006
INTRODUCCIÓN
La estimación de los caudales de diseño para el suministro de redes de agua potable en
edificaciones en nuestro país, se ha venido realizando por medio de la aplicación del método de
probabilidades de Roy Hunter; de acuerdo con estudios recientes realizados se ha demostrado que
los caudales de diseño difieren significativamente de los consumos reales en dichas edificaciones.
En el presente artículo se pretende recopilar y analizar algunos de los diferentes métodos
disponibles para la estimación de los caudales máximos probables y comparar los resultados
obtenidos con las demandas reales, con el fin de establecer la metodología que permita estimar con
mayor certeza los consumos reales.
MARCO TEÓRICO
1.
MÉTODOS DE CÁLCULO CAUDALES MÁXIMOS
El objeto principal de todos los métodos es determinar el caudal máximo probable que se puede
presentar en una instalación, sin embargo, es complicado establecer dicho valor debido a que los
muebles sanitarios son utilizados de forma intermitente, con frecuencias muy variadas y en
diferentes tipos de edificaciones.
En términos generales se han desarrollado tres metodologías para determinar los caudales o gastos
de diseño para las diferentes partes de un sistema de distribución de agua; los cuales se pueden
clasificar así:
1.1.
MÉTODOS EMPÍRICOS
En estos métodos, para un número dado de muebles sanitarios en un sistema, se toma una decisión
arbitraria, con base en la experiencia, en relación al número de muebles que pueden operar
simultáneamente. En teoría, los métodos empíricos podrían considerarse los mejores para el cálculo
de pequeños sistemas hidráulicos.
1.1.1.
Método Británico
Este método establece, con base en el criterio de un grupo de personas especializadas en el diseño
de sistemas hidráulicos, tablas de "Probables Demandas Simultáneas", correspondientes a diversas
cargas potenciales. La Tabla Nº 1 muestra las demandas para distintos muebles sanitarios; después,
considerando el sistema de distribución hidráulico, se sumaron las demandas de todos los muebles
sanitarios que puede servir una línea de tubería en el sistema, para luego ingresar a la Tabla Nº 2
con el número de litros por minuto que se calcularon, leer la Probable Demanda Máxima
Simultánea en litros por minuto, y diseñar la tubería que conducirá este flujo.
VI SEREA - Seminário Iberoamericano sobre Sistemas de Abastecimento Urbano de Água
João Pessoa (Brasil), 5 a 7 de junho de 2006
Tabla Nº 1. DESCARGAS APROXIMADAS PARA MUEBLES SANITARIOS
EN AGUA FRÍA Y AGUA CALIENTE1
MUEBLES
DESCARGA
SANITARIOS
(l.p.m)
Baño privado
18.93
Baño público
30.28
Lavadero
15.14
Lavamanos
7.57
Ducha
7.57
Regadera de 4”
15.14
Regadera de 6”
30.28
Válvulas de
57.00
fluxómetro*
* Caudal supuesto
Tabla Nº 2. Descargas simultáneas para muebles sanitarios2
DEMANDA
DEMANDA
GASTO TOTAL
GASTO
PROBABLE
PROBABLE
(l/m)
TOTAL (l/m)
(l/m)
(l/m)
100% del máximo
Hasta 12
318.0
147.6
posible
53.0
49.2
405.0
159.0
60.6
54.9
465.6
170.3
68.1
60.6
537.5
181.7
75.7
66.2
617.0
196.8
87.1
71.9
711.7
212.0
98.4
77.6
817.6
230.9
113.6
85.2
938.8
246.1
132.5
90.8
1082.8
268.8
151.4
98.4
1245.4
291.5
174.1
106.0
1430.9
321.8
200.6
113.6
1646.6
359.6
230.9
121.1
1892.7
393.7
20% del máximo
268.8
128.7
Más de 1892.7
posible
306.6
140.1
1.1.2.
Método de Dawson y Bowman
De manera análoga al método anterior, es el desarrollado por Dawson y Bowman en la Universidad
de Wisconsin. Ellos prepararon una tabla del número total de muebles sanitarios en varias clases de
vivienda unifamiliar y casas de apartamentos de hasta seis unidades de vivienda y especificaron el
número y la clase de muebles sanitarios que podrían estar en uso simultáneo para determinar las
cargas de diseño. En la Tabla Nº 3 se muestran los resultados que obtuvieron.
Para estimar el caudal máximo posible se tienen en cuenta los caudales individuales de la Tabla
Nº1.
VI SEREA - Seminário Iberoamericano sobre Sistemas de Abastecimento Urbano de Água
João Pessoa (Brasil), 5 a 7 de junho de 2006
1.2.
MÉTODOS SEMIEMPÍRICOS
Estos métodos, aunque se basan en la experiencia, tienen cierto sustento teórico, que les permite
establecer fórmulas y expresiones matemáticas.
1.2.1.
Método Alemán de la Raíz Cuadrada
Este método toma como unidad de gasto, la descarga de una llave de 3/8" (0.25 l.p.s) bajo ciertas
condiciones, y asigna un "factor de carga" unitario a dicho gasto.
Para cualquier otro mueble que tenga un gasto diferente, un factor de carga es establecido tomando
una relación entre el gasto de éste y el "gasto unitario" (llave de 3/8") y elevando al cuadrado el
resultado.
Así, el factor de carga para cada tipo de mueble en el edificio es multiplicada por el número de
muebles servidos por la tubería en cuestión, el resultado es sumado, y finalmente es obtenida la raíz
cuadrada. El resultado es multiplicado por el gasto unitario de una llave de 3/8" para obtener el
gasto de abastecimiento al edificio, cualquiera que éste sea. La obtención de la raíz cuadrada
considera, de una manera arbitraria, el hecho que los muebles no trabajan simultáneamente.
La metodología es como sigue:
Considere una unidad de flujo o gasto, la cual es tomada normalmente como la de una llave de 3/8".
Este gasto se asume que es de 0.25 l/s (4 g.p.m); esta unidad de gasto se denota con q1, y el factor
de carga f1 para la llave es tomado como unitario.
VI SEREA - Seminário Iberoamericano sobre Sistemas de Abastecimento Urbano de Água
João Pessoa (Brasil), 5 a 7 de junho de 2006
Tabla Nº 3. GASTOS DE DISEÑO RECOMENDADOS PARA PEQUEÑAS INSTALACIONES
HIDRÁULICAS EN EDIFICIOS DE APARTAMENTOS Y VIVIENDA UNIFAMILIAR3
TIPO DE
EDIFICIO
MUEBLES
GASTO TOTA GASTO DE DISEÑO
SANITARIOS
(l/min)
(l/min)
2 llaves exteriores
37.85
18.93
2 llaves de lavandería
60.56
30.28
1 llave de fregadero
28.39
Casa unifamiliar
1 lavabo
18.93
18.93
de familia pequeña
1 WC o inodoro*
11.36
11.36
1 tina o regadera
37.85
Sumatorias
195.84
79.50
2 llaves exteriores
37.85
18.93
2 llaves de lavandería
60.56
30.28
1 llave de fregadero
28.39
Casa unifamiliar
3 lavabos
56.78
18.93
de familia grande
3 WCs o inodoros*
34.07
11.36
2 tinas o regaderas
75.70
37.85
Sumatorias
293.35
117.35
2 llaves exteriores
37.85
18.93
4 llaves de lavandería
121.12
60.56
2 llaves de fregadero
56.78
28.39
Dos familias
2 lavabos
37.85
18.93
en una sola planta
2 WCs o inodoros*
22.71
11.36
2 tinas o regaderas
75.70
Sumatorias
352.01
138.17
2 llaves exteriores
37.85
18.93
6 llaves de lavandería
181.68
90.84
4 llaves de fregadero
113.55
56.78
Cuatro familias
4 lavabos
75.70
18.93
en apartamentos
4 WCs o inodoros*
45.42
22.71
4 tinas o regaderas
151.40
Sumatorias
605.60
208.19
2 llaves exteriores
37.85
18.93
8 llaves de lavandería
242.24
90.84
6 llaves de fregadero
170.33
81.38
Seis familias
6 lavabos
75.70
37.85
en apartamentos
6 WCs o inodoros*
68.13
22.71
6 tinas o regaderas
227.10
37.85
Sumatorias
821.35
289.56
*Todos los WC o inodoros se consideran de tanque. Si se utilizarán fluxómetros, úsese el
valor de 113.55 l/min en las columnas 3 y 4 del WC.
Ahora, considere que se tienen n1 llaves de este diámetro abastecidas por una tubería, cuya carga o
gasto de diseño quiere ser determinada. Si se asume que n1 de estos muebles pueden operar
simultáneamente en cualquier instante de observación, la carga de diseño será:
Q = q1 f1n1
VI SEREA - Seminário Iberoamericano sobre Sistemas de Abastecimento Urbano de Água
João Pessoa (Brasil), 5 a 7 de junho de 2006
Ahora, a manera de ilustración, se puede considerar que tenemos también n2 llaves de 3/4"
abastecidas por la misma línea. Se considera que una llave de 3/4" tiene una demanda de 0.75 l/s en
la tubería de abastecimiento, esto es, consume un gasto tres veces mayor que la llave de 3/8". El
factor de carga f2 para la llave de 3/4" será 32 = 9.
Generalizando, para cualquier clase de muebles que son usados de manera intermitente en el
sistema, tenemos como fórmula para la carga de diseño, la siguiente:
Q = q1 f 1 n1 + f 2 n 2 + ⋅ ⋅ ⋅ + f i ni
Donde;
Q = carga o gasto de diseño, en l.p.s.
f1, f2, fn = factor de carga.
n1, n2, ni = número de muebles sanitarios por clase.
1.2.2.
Método del Factor de Simultaneidad
Para la obtención del caudal máximo probable (Qp) se hace preciso establecer los caudales de los
aparatos instalados, sumarlos y, posteriormente, afectar los resultados por un coeficiente de
simultaneidad K1.
K1 =
1
(n − 1)
Esta fórmula es la establecida por la Norma Francesa NP 41-204 para toda clase de edificios. Los
caudales mínimos recomendados se muestran en la Tabla Nº 4.
Tabla Nº 4. CAUDALES MÍNIMOS PARA CADA APARATO.4
Qmín
APARATO
(lt/seg)
Calentador Eléctrico
0,30
Ducha
0,20
Inodoro de Tanque
0,15
Inodoro de
0.95
Fluxómetro
Lavamanos
0,20
Lavadero
0.20 – 0.30
Lavaplatos
0.25 – 0.30
Lavadora
0.20 – 0.30
Llave Externa
0,25
entonces Qp será:
QP = K1 × qmáx
De diferentes congresos internacionales sobre el tema se ha concluido por conveniencia que K1 en
ningún caso será inferior a 0,2; aunque es una condición que puede ser revaluada.
VI SEREA - Seminário Iberoamericano sobre Sistemas de Abastecimento Urbano de Água
João Pessoa (Brasil), 5 a 7 de junho de 2006
1.2.3.
Método Racional o Español5
Al igual que en el caso anterior se establecen los caudales de los aparatos instalados, se suman y se
afectan los resultados por el coeficiente de simultaneidad K1, pero en éste caso n será el número de
aparatos instalados en una vivienda;
K1 =
1
(n − 1)
En conjuntos de viviendas de similares características, para considerar la simultaneidad, el caudal
punta QP del distribuidor común a un determinado número de las mismas se obtiene como la
sumatoria de los caudales puntas de cada vivienda qp afectado por el siguiente factor:
K2 =
( N + 19)
10 * ( N + 1)
Donde N, es el número de viviendas.
Para una buen funcionamiento de los aparatos, en la Tabla Nº 5 se muestran los caudales mínimos
que se deben suministrar.
Tabla Nº 5. CAUDALES MÍNIMOS MÉTODO RACIONAL
P
APARATO
Q
(Kg/cm2 P
(lt/seg)
(mca)
)
Lavabo
0,10
0,35 3,50
Sanitario con
0,10
0,35 3,50
depósito
Ducha
0,20
1,00 10,00
Lavadero
0,20
0,35 3,50
Lavadora
0,20
Lavaplatos
0,20
Llave Exterior
0,25
Fregadero
0,20
0,35 3,50
Bidet
0,10
0,35 3,50
Bañera
0,30
1,00 10,00
"Oficce"
0,15
0,35 3,50
0.95 Fluxómetros
1,00 10,00
2,0
Nota: Según normatividad española
1.3.
METODOS PROBABILISTICOS
La teoría de la probabilidad, aunque es la más racional, es de dudosa aplicación cuando se trata del
diseño de instalaciones hidráulicas en edificios con escasos muebles sanitarios; además, las
frecuencias de uso consideradas en el método probabilístico de Hunter, son demasiado altas para
este tipo de diseño.
VI SEREA - Seminário Iberoamericano sobre Sistemas de Abastecimento Urbano de Água
João Pessoa (Brasil), 5 a 7 de junho de 2006
1.3.1.
Método de Hunter6
Para el dimensionamiento de las tuberías se tiene en cuenta que todos los aparatos instalados no
funcionan simultáneamente; por esta razón se deben distinguir varios tipos de caudal.
El método pretende evaluar el caudal máximo probable y se basa en el concepto de que únicamente
unos pocos aparatos, de todos los que están conectados al sistema, entrarán en operación simultánea
en un instante dado. El efecto de cada aparato que forma parte de un grupo numeroso de elementos
similares, depende de:
•
•
•
Caudal del aparato, o sea la rata de flujo que deja pasar el servicio (q).
Frecuencia de uso: tiempo entre usos sucesivos (T).
Duración de uso: tiempo que el agua fluye para atender la demanda del aparato (t).
El método es aplicable a grandes grupos de elementos, ya que la carga de diseño es tal que tiene
cierta probabilidad de no ser excedida (aunque lo puede ser en pocas ocasiones).
Según Hunter, se tiene en funcionamiento satisfactorio cuando las tuberías están proporcionadas
para suministrar la carga de demanda para el número m del total de n aparatos del edificio, de tal
forma que no más de m serán encontrados en uso simultáneo por más del 1% del tiempo.
Si se considera que en una instalación de n aparatos, un número m de éstos se encuentre en
funcionamiento simultáneo por más del 1% del tiempo, se puede expresar así:
p0 + p1 + p 2 + ..... + p m−1 + pm = 0,99
P es la probabilidad de no encontrar ningún aparato funcionando. Los términos faltantes de la serie
son:
P =
∑
r=n
r=m1
 n 
  (1 − p
 r 
)n − r
p
r
≤ 0 , 01
que corresponde a la forma dada en las tablas de distribución binomial de probabilidades, excepto
que la expresión (1 - p) reemplaza al término q de las tablas.
El caudal de diseño se determina de acuerdo con;
Qdiseño = m × q
donde q es el caudal promedio que utiliza uno de los aparatos supuestos.
Hunter se ideó la forma de aplicar el método a sistemas con aparatos de diferente clase asignando el
peso o influencia de un aparato con respecto a los demás; entonces, el número que identifica un
aparato será una relación del número de válvulas de fluxómetro que producen un caudal
determinado al número de aparatos de otro tipo que producen el mismo caudal.
Unidades para un aparato =
Número de Fluxómetros
× Unidades asignadas al fluxómetro
No. de aparatos de otro tipo
VI SEREA - Seminário Iberoamericano sobre Sistemas de Abastecimento Urbano de Água
João Pessoa (Brasil), 5 a 7 de junho de 2006
Los valores aceptados por la mayoría de códigos para los diferentes aparatos se muestran en la
Tabla Nº 6.
Privado
Público
Tabla Nº 6. UNIDADES DE DIFERENTES APARATOS
Aparato o
Tipo
Tipo de
Unidades de Aparato
Grupo
de uso
Suministro
Agua Caliente Agua Fría
Sanitario
Fluxómetro
10
Sanitario
Tanque
5
Orinal Pedestal
Fluxómetro 1”
10
Orinal Pared
Fluxómetro 3/4”
5
Lavamanos
1.5
1.5
Tina
3
3
Regadera ducha
Mezclador
3
3
Lavaplatos
Mezclador
3
3
Sanitario
Fluxómetro
6
Sanitario
Tanque
3
Lavamanos
Mezclador
0.75
0.75
Tina
Mezclador
1.5
1.5
Regadera ducha
Mezclador
1.5
1.5
Grupo de Baño
Sanitario Flux
2.25
6.75
Grupo de Baño
Sanitario Tanque
2.25
4.5
Lavaplatos
Mezclador
1.5
1.5
Lavadora
2.25
2.25
1.3.2.
Total
10
5
10
5
2
4
4
4
6
3
1
2
2
8
6
2
3
Método de Hunter Modificado
Consumo Probable ( l/min )
Este método se deriva del anterior; y la obtención de las unidades de consumo se realiza de forma
idéntica; la modificación se da en la lectura del caudal máximo probable, que se halla de las figuras
1 y 27; donde se realiza una reducción del caudal promedio de los aparatos respecto del que usa el
método original.
Unidades de consumo (x 100)
Instalaciones con Fluxómetro
Instalaciones sin Fluxómetro
Figura Nº 1.a. CURVA DE DEMANDA HUNTER MODIFICADO
Consumo Probable ( l/min )
VI SEREA - Seminário Iberoamericano sobre Sistemas de Abastecimento Urbano de Água
João Pessoa (Brasil), 5 a 7 de junho de 2006
Unidades de consumo (x 10)
Instalaciones con Fluxómetro
Instalaciones sin Fluxómetro
Figura Nº 1.b. CURVA DE DEMANDA HUNTER MODIFICADO
APLICACIÓN DE LOS MÉTODOS A EDIFICACIONES DE DIFERENTE TIPO
Los métodos explicados anteriormente, se aplicaron a ocho (8) edificios de los que se conoce el
caudal máximo demandado, en total se evaluaron seis (6) métodos; Británico, Alemán de la Raíz
Cuadrada, Simultaneidad, Racional o Español, Hunter y Hunter Modificado; aunque se estudiaron
los métodos de Certeza Total, Presunción del Gasto y el de Dawson y Bowman; pero no se
consideraron para los cálculos porque no son adecuados para las edificaciones en estudio.
Los edificios que se han considerado son; de conjuntos residenciales, Takay II, Santa María del
Campo; de oficinas, Lago 76; todos ellos ubicados en la ciudad de Bogotá y los edificios de
Biblioteca Central, Odontología, Ciencias Humanas, Aulas de Ingeniería y Medicina de la
Universidad Nacional de Colombia sede Bogotá.
En la Tabla Nº 7 se muestran los resultados obtenidos una vez aplicado cada uno de los métodos y
se contrasta con el caudal aforado en cada edificio; en la Figura Nº 2 se muestran estos mismos
resultados gráficamente.
VI SEREA - Seminário Iberoamericano sobre Sistemas de Abastecimento Urbano de Água
João Pessoa (Brasil), 5 a 7 de junho de 2006
Tabla Nº 7. RESUMEN DE RESULTADOS APLICACIÓN DE LOS MÉTODOS.
EDIFICIOS
MÉTODOS Taka El SMD Bibliotec Odontolo Ciencias Aulas de Medici
Lago
a
Humana Ingenierí
y II
C
gía
na
76
Central
s
a
8,52 3,72 20,79 7,46
9,02
9,40
8,64
15,70
Hunter
Hunter
6,42 2,83 16,00 5,67
6,67
6,92
6,33
11,33
Modificado
11,1
3,33 34,62 7,55
11,22
12,51
10,32 24,91
Británico
0
Raíz
9,49 4,61 17,15 9,89
16,61
12,39
11,62 17,46
Cuadrada
17,2
2,99 52,92 7,53
12,59
12,41
10,19 21,98
Simultaneidad
0
2,68 1,22 6,25 4,41
3,66
6,04
4,82
6,87
Racional
3,12 0,86 3,24 0,34
2,28
1,11
0,97
1,72
Aforado
Es preciso anotar que en los 40 apartamentos del conjunto residencial Takay II cada uno cuenta con
2 baños completos (Ducha, Lamanos e Inodoro) y lavadora, lavadero y lavaplatos; las casas de
Santa María del Campo tiene 3 baños completos, lavadora, lavadero y lavaplatos con un total de 98
casas; en el edificio Lago 76 se tienen 42 oficinas cada una con un lavamanos y un inodoro. Los
edificios universitarios presentan instalaciones más complejas y se encuentran gran número de
válvulas de fluxómetro, además en algunos se encuentran instalaciones adecuadas para las prácticas
estudiantiles como es el caso de los edificios de medicina y odontología.
Si se observa cuidadosamente los valores de la Tabla Nº 7 o la Figura Nº 2 se encuentra que para
cada una de las edificaciones por los diferentes métodos, el caudal de diseño varía ampliamente y
en la mayoría de los casos el caudal calculado excede significativamente el caudal medido (excepto
para Takay II por Método Racional, donde es inferior). Los métodos que presentan un mayor
acercamiento al caudal aforado son en su orden el método Racional, Hunter Modificado y Hunter
Original.
VI SEREA - Seminário Iberoamericano sobre Sistemas de Abastecimento Urbano de Água
João Pessoa (Brasil), 5 a 7 de junho de 2006
60
Hunter
Hunter Modificado
50
Británico
Raíz Cuadrada
Simultaneidad
40
Caudal (l/s)
Racional
Aforado
30
20
10
0
Takay II
El Lago 76
SMDC
Biblioteca Central
Odontología
Ciencias Humanas
Figura Nº 2. RESUMEN GRÁFICO DE RESULTADOS.
Aulas de Ingeniería
Medicina
VI SEREA - Seminário Iberoamericano sobre Sistemas de Abastecimento Urbano de Água
João Pessoa (Brasil), 5 a 7 de junho de 2006
CONCLUSIONES Y RECOMENDACIONES
Una de las variables con mayor incidencia en los resultados es el caudal de funcionamiento de cada uno
de los aparatos o el caudal promedio según sea el caso; en general los métodos más antiguos consideran
caudales altos generando un sobredimensionamiento en las instalaciones.
El método que más se acerca a la aproximación del caudal máximo real en todos los casos es el Método
Racional; cabe anotar que para el edificio residencial Takay II se obtiene un caudal de diseño un 14%
más bajo que el medido; dicha aproximación se debe a los bajos caudales de funcionamiento que
considera y al factor K2; es preciso anotar que éste factor no presenta un modelo matemático o
probabilístico que lo sustente y es muy subjetiva su aplicación, en particular en los edificios donde no
se tiene uniformidad en la distribución de los conjuntos de aparatos.
Si se tienen en cuenta los resultados mostrados se observa que la aplicación del método Racional es
una buena alternativa en el diseño de éste tipo de instalaciones, pero se debe tener cuidado con las
consideraciones, pues el caudal calculado varía ampliamente con los factores K1 y K2; y por tanto la
incertidumbre sobre los resultados obtenidos.
En los edificios estudiados de la Ciudad Universitaria se presume que los caudales máximos medidos
son muy bajos para el uso masivo que se puede esperar en este tipo de edificaciones, por ejemplo en la
Biblioteca Central el caudal medido es de 0.34 l/s el cual en teoría no cumple ni con el mínimo
requerido por una válvula de fluxómetro; es una de las razones por la que los caudales calculados
difieren significativamente de los aforados.
NOMENCLATURA
Q (l.p.s): Carga o gasto de diseño.
f1, f2, fn : Factor de carga.
n1, n2, ni : Número de muebles sanitarios por clase.
Qp (l.p.s): Caudal máximo probable
K1 : Coeficiente de simultaneidad
n: Número de aparatos instalados en una vivienda
m: Número de aparatos instalados en la vivienda en funcionamiento
N: Número de viviendas
q (l.p.s): Caudal del aparato, o sea la rata de flujo que deja pasar el servicio.
T (s): Frecuencia de uso
t (s): Duración de uso: tiempo que el agua fluye para atender la demanda del aparato.
BIBLIOGRAFÍA
GARCIA SOSA, JORGE.. “Instalaciones Hidráulicas y Sanitarias en Edificios”. México. 2001
MELGUIZO.”Instalaciones Hidráulicas y Sanitarias”. Vol 1. Medellín.
GRANADOS, JORGE. “Redes Hidráulicas y Sanitarias en Edificios”. UNIBIBLOS. Bogotá. 2002.
INSTITUTO COLOMBIANO DE NORMAS TÉCNICAS. Norma 1500 “Código Colombiano de
Fontanería”. Figura Nº 9 Curva de demanda. ICONTEC. 1979.
VI SEREA - Seminário Iberoamericano sobre Sistemas de Abastecimento Urbano de Água
João Pessoa (Brasil), 5 a 7 de junho de 2006
1
GARCIA SOSA, Jorge. Instalaciones Hidráulicas y Sanitarias en Edificios. México. 2001.
Idem
3
GARCÍA SOSA, Jorge. Instalaciones Hidráulicas y Sanitarias en Edificios. México. 2001.
4
MELGUIZO. Instalaciones Hidráulicas y Sanitarias. Vol 1. Medellín.
5
Tomado de Gallizio, en Roca y Carratala 2002.
6
GRANADOS, Jorge. Redes Hidráulicas y Sanitarias en Edificios. UNIBIBLOS. Bogotá. 2002.
7
INSTITUTO COLOMBIANO DE NORMAS TÉCNICAS. Norma 1500 “Código Colombiano de Fontanería”. Figura 9
Curva de demanda. ICONTEC. 1979.
2