Tema 3. GeoGebra aplicado a geometría analítica GeoGebra

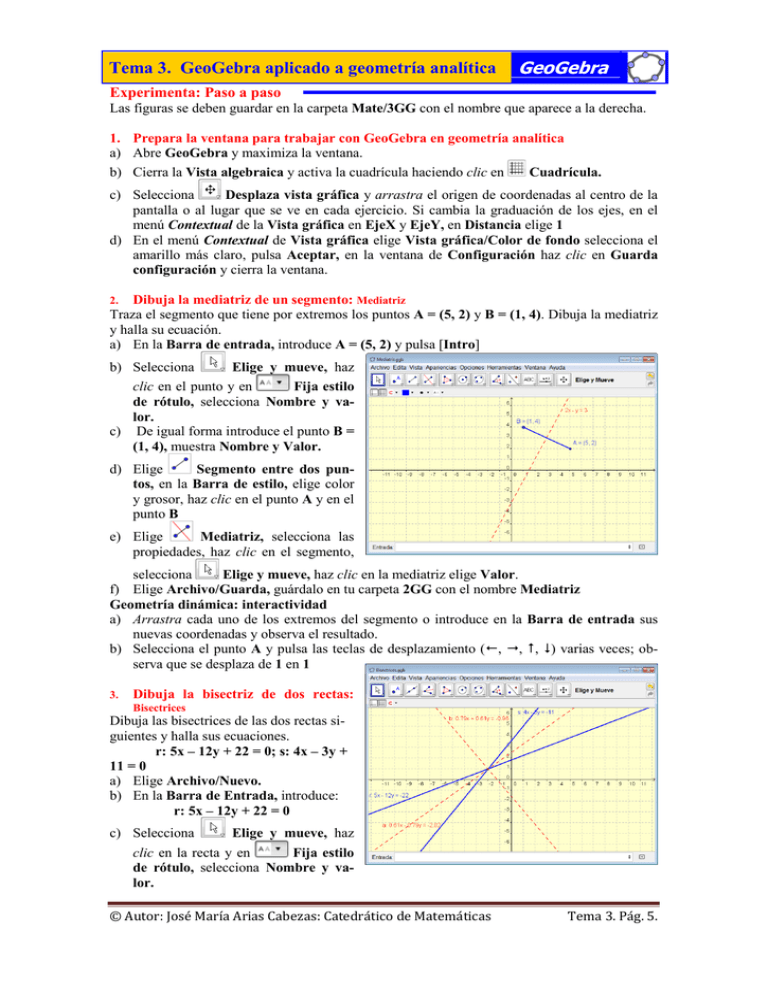
Tema 3. GeoGebra aplicado a geometría analítica
GeoGebra
Experimenta: Paso a paso
Las figuras se deben guardar en la carpeta Mate/3GG con el nombre que aparece a la derecha.
1. Prepara la ventana para trabajar con GeoGebra en geometría analítica
a) Abre GeoGebra y maximiza la ventana.
b) Cierra la Vista algebraica y activa la cuadrícula haciendo clic en
Cuadrícula.
c) Selecciona
Desplaza vista gráfica y arrastra el origen de coordenadas al centro de la
pantalla o al lugar que se ve en cada ejercicio. Si cambia la graduación de los ejes, en el
menú Contextual de la Vista gráfica en EjeX y EjeY, en Distancia elige 1
d) En el menú Contextual de Vista gráfica elige Vista gráfica/Color de fondo selecciona el
amarillo más claro, pulsa Aceptar, en la ventana de Configuración haz clic en Guarda
configuración y cierra la ventana.
Dibuja la mediatriz de un segmento: Mediatriz
Traza el segmento que tiene por extremos los puntos A = (5, 2) y B = (1, 4). Dibuja la mediatriz
y halla su ecuación.
a) En la Barra de entrada, introduce A = (5, 2) y pulsa [Intro]
2.
b) Selecciona
Elige y mueve, haz
clic en el punto y en
Fija estilo
de rótulo, selecciona Nombre y valor.
c) De igual forma introduce el punto B =
(1, 4), muestra Nombre y Valor.
d) Elige
Segmento entre dos puntos, en la Barra de estilo, elige color
y grosor, haz clic en el punto A y en el
punto B
e) Elige
Mediatriz, selecciona las
propiedades, haz clic en el segmento,
selecciona
Elige y mueve, haz clic en la mediatriz elige Valor.
f) Elige Archivo/Guarda, guárdalo en tu carpeta 2GG con el nombre Mediatriz
Geometría dinámica: interactividad
a) Arrastra cada uno de los extremos del segmento o introduce en la Barra de entrada sus
nuevas coordenadas y observa el resultado.
b) Selecciona el punto A y pulsa las teclas de desplazamiento (, , , ) varias veces; observa que se desplaza de 1 en 1
3.
Dibuja la bisectriz de dos rectas:
Bisectrices
Dibuja las bisectrices de las dos rectas siguientes y halla sus ecuaciones.
r: 5x – 12y + 22 = 0; s: 4x – 3y +
11 = 0
a) Elige Archivo/Nuevo.
b) En la Barra de Entrada, introduce:
r: 5x – 12y + 22 = 0
c) Selecciona
Elige y mueve, haz
clic en la recta y en
Fija estilo
de rótulo, selecciona Nombre y valor.
© Autor: José María Arias Cabezas: Catedrático de Matemáticas
Tema 3. Pág. 5.
d) Dibuja de igual forma la recta s
e) Elige
Bisectriz y haz clic en la recta r y en la recta s
f) Muestra en las dos bisectrices el nombre y el valor.
Geometría dinámica: interactividad
a) En la ventana Algebraica, modifica una de las ecuaciones de las rectas y verás cómo cambian las bisectrices y sus ecuaciones. También puedes introducir las nuevas ecuaciones en la
Barra de entrada.
4. Dibuja el circuncentro de un triángulo: Circuncentro
Dibuja el triángulo que tiene como vértices los puntos A = (6, 2), B = (1, – 3) y C = (– 3, 5).
Halla las mediatrices de sus lados, sus ecuaciones, el circuncentro, la circunferencia circunscrita
y su ecuación.
a) En la Barra de entrada, introduce uno a
uno los siguientes puntos que son los vértices del triángulo A = (6, 2), B = (1, – 3) y
C = (– 3, 5)
b) Dibuja el triángulo ABC
c) Dibuja las mediatrices.
d) Halla las ecuaciones de las mediatrices.
e) Halla el circuncentro como intersección de
dos mediatrices.
f) Muestra las coordenadas del circuncentro.
g) Dibuja la circunferencia circunscrita.
h) Halla la ecuación de la circunferencia circunscrita.
Geometría dinámica: interactividad
a) Arrastra un vértice del triángulo, modifica sus coordenadas en la ventana Algebraica o introduce en la Barra de entrada las nuevas coordenadas y observa los resultados.
b) Introduce, en la Barra de entrada, los nuevos vértices A = (7, –1), B = (4, 8) y C = (–1, 3)
Recta definida por un punto y un vector director: RectaPv
Dibuja la recta que pasa por el punto P = (– 5, 2) y cuyo vector director es v(3, 2). Halla la
ecuación de la recta.
a) En la Barra de entrada, introduce P = (– 5,
2)
5.
b)
Elige
Vector entre dos puntos. Haz
clic en el origen de coordenadas y en el extremo del vector v(3, 2). Renómbralo como
v y muestra su valor.
c) Elige
Recta paralela, haz clic en el
punto P y en el vector v
d) Muestra su ecuación.
Geometría dinámica: interactividad
a) Arrastra el punto P, modifica sus coordenadas en la Ventana algebraica o introdúcelas en
la Barra de entrada. Observa cómo se obtienen la nueva recta y su ecuación.
b) Arrastra el extremo del vector v, modifica sus coordenadas en la Ventana algebraica o
introdúcelas en la Barra de entrada. Observa cómo se obtienen la nueva recta y su ecuación.
c) Teniendo seleccionado el punto P, mantén pulsada la tecla [Ctrl] y pulsa las teclas de desplazamiento varias veces; observa que se desplaza de 1 en 1
© Autor: José María Arias Cabezas: Catedrático de Matemáticas
Tema 3. Pág. 6.