Biocinética y Bioreactores

Biocinética y Bioreactores
¿Qué hace a un reactor biológico distinto a un reactor convencional? ¿Cómo trasladamos lo que
ya sabemos sobre reactores químicos para ahora entender, analizar, diseñar y optimizar reactores
biológicos? Bien, comencemos por decir que, desde el punto de vista de tratamiento formal, no
hay diferencias apreciables. Al igual que para el caso de los reactores “convencionales” en el
análisis de los reactores biológicos nos valemos de ecuaciones de diseño (derivadas del balance
de masa correspondiente) y en ellas introducimos un término de producción (o consumo) que
derivamos de leyes cinéticas. Si, el proceso matemático es análogo, y el propósito el mismo
(maximizar conversión del producto deseado, si hay más de un producto favorecer la
selectividad hacia el producto deseado, optimizar la temperatura de operación, etc.
¿Dónde están entonces las diferencias? Pues en las expresiones cinéticas. Los modelos cinéticos
que hemos visto hasta el momento no necesariamente reproducen aceptablemente el
comportamiento de reacciones biológicas. Estriba en esto la sutil gran diferencia. Claro que,
detrás de esta diferencia en el tratamiento matemático hay una distinción mas fundamental. En
un bioreactor trabajamos con organismos vivos o con partes de organismos vivos (enzimas) que
poseen características muy particulares.
Comencemos por el modelo cinético más característico de una reacción bioquímica, el modelo
de Michaelis-Menten para cinética enzimática. ¿Por qué es este el modelo más característico?
Todas las reacciones bioquímicas, así sean llevadas a cabo en un bioreactor industrial, dentro de
una célula o fuera de ella, dentro de tu cuerpo o en un tejido animal o vegetal, son mediadas por
enzimas. Las enzimas son proteínas que actúan como catalizadores. Facilitan el acontecimiento
de reacciones que de otra forma, en su ausencia, estarían muy impedidas energéticamente (serían
muy lentas o termodinámicamente imposibles a condiciones normales de P y T). Por citar un
ejemplo trivial, la combustión de un carbohidrato (azúcar) requiere de altas temperaturas para
Ingeniería de Reactores
62
M.Alvarez 2003
ocurrir. Sin embargo, el proceso de respiración celular (que no es más que una combustión) se
lleva a cabo de forma muy eficiente y a T = 37°C cuando es mediado por enzimas presentes en
nuestras mitocondrias. Las enzimas son moléculas tridimensionales muy complejas y flexibles,
que por diversos mecanismos reducen la energía de activación necesaria para una reacción. En
verdad son catalizadores, pues posibilitan las reacciones pero no se involucran en ellas como
reactivos. Es momento de que introduzcamos aquí un poco de nomenclatura.
Sustrato: Es el reactivo o reactivos que la enzima procesará.
Producto: No hay mayor problema, es el producto de la reacción.
Complejo Enzima-Sustrato: Es el complejo activado de una reacción enzimática. En este
estado transitorio, la enzima y el sustrato se encuentran unidos, ya sea por atracciones
electrostáticas, o inclusive en algunos casos covalentemente. Este complejo activado es
reversible y transitorio.
Sitio activo: Localidad de la enzima donde físicamente se lleva a cabo la reacción. Normalmente
al sitio activo se une el sustrato (de una forma altamente específica) y es ahí donde se
llevan a cabo las transformaciones químicas.
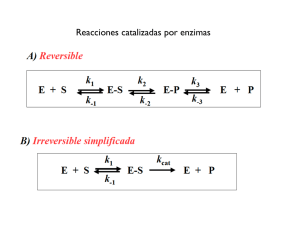
La figura 1, esquematiza en forma muy simplista, como actúa una enzima. Este modelo o
mecanismo fue propuesto a principios del siglo XX. Está compuesto por tres etapas (aunque
luego introduciremos una simplificación). En la primera etapa la enzima y el sustrato se
encuentran, uno a uno, y se realiza un acoplamiento. Nótese que esta etapa del mecanismo es
reversible, y está mediada entonces por una constante de velocidad en cada dirección (a las que
llamaremos k1 y k2). La segunda etapa es aquella en donde se realiza la transformación química.
El sustrato pasa a producto en el seno de la enzima, en el sitio activo. En la tercera etapa, la
enzima libera al producto, quedando disponible para un posterior encuentro con otra molécula de
sustrato.
Hagamos algunas simplificaciones y algunas suposiciones. Supongamos que la segunda y tercera
etapa pueden ser sintetizadas en una sola. Formulemos entonces que todo el proceso puede ser
descrito por los dos pasos ilustrados en la figura 2. Ya con esta simplificación, derivaremos un
modelo matemático consistente con ciertas observaciones experimentales. Como primer paso en
Ingeniería de Reactores
63
M.Alvarez 2003
la derivación, supondremos que la primera etapa del mecanismo ocurre rápidamente, y
rápidamente llega al equilibrio. Es decir:
k1[E][S] = k2 [ES]
(1)
En consecuencia, la segunda etapa del mecanismo es la etapa lenta, y por tanto la limitante.
Luego, la velocidad del proceso global (rs) deberá estar correctamente descrito por:
rs = k3 [ES]
(2)
Este es un modelo que correctamente describiría a una reacción enzimática típica bajo las
suposiciones que hemos hecho. Hay solo un problema. Como recordarás, es recomendable
expresar ecuaciones cinéticas en términos de constantes y concentraciones (o presiones
parciales) que podemos calcular o medir. Desgraciadamente, en este modelo sencillo de primer
orden en [ES] no se cumple este requisito, pues ES es un complejo transitorio difícilmente
medible. Esto nos lleva a la necesidad de buscar substituir la concentración de ES por otras
variables que si podamos monitorear. Para lograr esto, recurriremos al siguiente argumento:
El intermediario ES, precisamente por su naturaleza intermediaria, no se acumula con respecto al
tiempo y por tanto, en estado estacionario podemos escribir este balance:
d[ES]
= k 1 [E][S] − k 2 [ES] − k 3 [ES] = 0
dt
(3)
Reagrupando este balance diferencial se puede llegar a la expresión:
Ingeniería de Reactores
64
M.Alvarez 2003
Esta expresión por si sola no es muy útil, pues contiene el término de enzima libre [E] que
difícilmente puede ser medido durante la reacción. Afortunadamente podemos recurrir a una
argucia matemática. Consideremos un balance global de enzima. La enzima inicialmente
dispuesta para la reacción será en todo momento igual a la suma entre la enzima libre y la
enzima acomplejada con el sustrato. Entonces:
[Eo] = [E]+[ES]
(4)
Substituyendo la ecuación (4) en la ecuación (3) podemos deshacernos de [E]:
k1{[Eo] − [ES]}[S] = [ES](k2 + k3)
(5)
Aún más, en la ecuación 5, convenientemente, podemos despejar [ES] dejándola en función de
constantes cinéticas y valores de concentraciones que si podemos medir: [Eo], [S].
k1[Eo][S] − k1[ES][S] = [ES] (k2+k1)
k1[Eo][S] = [ES]{(k2+k1)+(k1[S]}
[ES] =
k 1 [Eo][S]
k 2 + k 3 + k 1 [S]
(6)
Y substituyendo (6) en (2)
rs =
k 3 k 1 [Eo][S]
k 2 + k 3 + k 1 [S]
Dividiendo ahora arriba y abajo entre k1 llegamos a la expresión (7)
rs =
k 3 [Eo][S]
(k 2 + k 3 ) / k 1 + [S]
(7)
Y si a k3[Eo] le llamamos velocidad máxima (rmax), y a (k2+k3)/k1 le llamamos Km, entonces
habremos derivado la famosa ecuación típica para cinética enzimática, la ecuación de MichaelisMenten:
rs =
rmax [S]
K m + [S]
(8)
Ya tenemos entonces una expresión que refleja el mecanismo propuesto en la Figura 2. Son esta
expresión y su mecanismo válidos. Bueno, la experiencia ha demostrado que bien reproducen
resultados experimentales como el que presentado en la Figura 3. En tal figura, se te presentan
datos de concentración de velocidad de la enzima con respecto al tiempo. Nótese que en tal
Ingeniería de Reactores
65
M.Alvarez 2003
gráfica se refiere al punto de concentración donde la velocidad alcanza la mitad de rmax como Km.
Puedes corroborar matemáticamente que esto es cierto?
Pues si ya tenemos nuestra expresión cinética, estamos listos para comenzar a diseñar reactores.
Veamos por ejemplo el caso de un reactor enzimático operado en forma batch, donde el sustrato
glucosa se convierte en fructosa (como probablemente sabes, los jarabes fructosados son mas
dulces y tienen mayor valor comercial que los jarabes de glucosa). La ecuación de diseño para
un reactor batch sigue siendo la misma, pues proviene del balance de materia sobre el sustrato en
el reactor. Al no entrar ni salir sustrato, el balance, como en un reactor batch convencional, solo
incluye los términos de acumulación y producción.
−
r [S]
d[S]
= rs = max
K m + [S]
dt
Como siguiente paso en nuestra discusión, mencionaremos como evaluar los parámetros
cinéticos de la ecuación (8), rmax y Km. La ecuación de velocidad se puede re-arreglar de varias
formas para expresarla como una línea recta.
Tres formas de linearización de la ecuación de Michaelis-Menten (M-M) son comunes:
[S] K m [S]
=
+
rs
rmax rmax
K 1
1
1
(b)
=
+ m
rs rmax rmax [S]
r
(c) rs = rmax − K m s
[S]
(9)
(a)
(10)
(11)
Por cualquiera de estas tres formas (cada una presenta sus ventajas y desventajas), es posible
encontrar los parámetros cinéticos a través de los valores de la pendiente y la intersección con la
abscisa.
Por ejemplo, tomemos la segunda ecuación. Según esta, una gráfica de la variable independiente
1/[S] contra la variable dependiente (1/rs) nos daría una línea recta al graficar datos
experimentales si en verdad el proceso correspondiera a una cinética M-M. La intersección de
esta línea recta con la abcisa sería el inverso del valor de rmax. Ya teniendo este podemos calcular
también el valor de Km, puesto que el valor de pendiente de la recta es precisamente Km/rmax.
Ingeniería de Reactores
66
M.Alvarez 2003
Consideremos los siguientes datos experimentales. De una serie de corridas en reactores batch a
distintas concentraciones de glucosa (sustrato) se han calculado los siguientes datos de velocidad
inicial de conversión de glucosa a fructosa:
Experimento
(R. Batch)
1
2
3
4
5
6
7
8
[So]
(mmol/L)
1
2
3
5
7
10
15
20
rso
mmol/(L min)
0.20
0.22
0.30
0.45
0.41
0.50
0.40
0.33
Data_Biorxn_clase
5.5
y = 2. 2249 + 3 .0387 x R = 0.884 67
5
4.5
4
1/v
3.5
3
2.5
2
1.5
0
0.2
0.4
0.6
0.8
1
1.2
1/ [S]o
Así, 1/rmax = 2.2249. Entonces rmax = 0.4494 mmol/(L min). La pendiente de la recta descrita por
los datos experimentales es 3.0387. Este valor es igual a Km/rmax, de donde Km = 3.0387×0.4494
= 1.3657 mmol/L
El método de cálculo de valores cinéticos basado en experimentos en reactores batch es el más
práctico. Aunque hay forma de calcular rmax y Km con experimentos en reactores continuos, el
método de velocidades iniciales en batch es el mas simple de operar.
Ingeniería de Reactores
67
M.Alvarez 2003
Una vez obtenidos los parámetros cinéticos, podemos dimensionar bioreactores. Por ejemplo,
supongamos que queremos calcular el tiempo que deberemos procesar una solución de glucosa
de 10 mmol/lt hasta un 90% de conversión en un reactor batch. El balance de materia sería:
−
r [S]
d[S]
= max
dt
K m + [S]
(12)
Separando variables e integrando:
[ S]
∫
K m + [S]
−
d[S] =
[
S
]
[ S ]o
La solución de esta integral es:
K m ln
∫
t
rmax dt
0
[S]0
+ [S]0 − [S] = rmax t
[S]
(13)
Que es la ecuación que podremos utilizar para calcular el tiempo de residencia de nuestro
bioreactor enzimático.
¿Y para un reactor continuo tipo tanque? La ecuación de balance sobre sustrato (suponiendo
densidad constante, v0 = v) es:
v 0 [S]0 − v 0 [S] − rs V = V
d[S]
dt
(14)
Considerando estado estacionario, el término de acumulación se elimina:
v0
r [S]
([S]0 − [S]) = rs = max
V
K m + [S]
(15)
El factor (v0/V) es el inverso del tiempo espacial (τ), también conocido como velocidad espacial
(s), entonces:
r [S]
1
([S]0 − [S])
= max
τ K m + [S]
(16)
que sería la ecuación de diseño para un reactor enzimático continuo.
Ahora bien, en muchas situaciones prácticas no utilizamos directamente a una enzima aislada,
sino a todo un microorganismo vivo para realizar una reacción biológica. Si este es el caso,
entonces nuestro problema de diseño resulta aún más interesante. Ahora el biocatalizador no es
una enzima sino toda una célula. Las células se reproducen una vez provistas condiciones de T,
pH, concentración de nutrientes adecuadas, lo que significa que la concentración del
“biocatalizador” también puede varíar con respecto al tiempo. Para un bioreactor batch donde
estamos creciendo células, por ejemplo células de levadura, el balance sobre la biomasa (X) se
vería así:
Ingeniería de Reactores
68
M.Alvarez 2003
d[X ]
= µ[X]
dt
(17)
Este balance es consistente con el hecho de que la velocidad de incremento de biomasa (masa
celular) es dependiente de la biomasa celular misma existente en un cierto momento. Nótese que
si [X] tiene unidades de g células/mL, y t unidades de s, entonces µ tiene unidades de 1/s (µ es la
tasa de crecimiento específico para esa célula). Ahora bien, esa tasa de crecimiento no es
constante, sino que depende de la concentración de alimento de que dependa la célula y de
parámetros cinéticos propios. Si suponemos que todo el funcionamiento de la célula depende de
enzimas, y que es la más lenta de estas la que determina la tasa de crecimiento, entonces
podemos pensar en que µ tenga la forma de una ecuación M-M. De hecho, esa suposición es
ampliamente utilizada. La ecuación (18) es llamada ecuación de Monod, y es análoga a la
ecuación de Michaelis-Menten:
µ [S]
(18)
µ = max
K m + [S]
Y sustituyendo en (17) llegamos a:
d[X] µ max [S][X]
=
dt
K m + [S]
(19)
Desde luego este es solo uno de los balances pertinentes al análisis de un reactor celular.
Podríamos, y en muchas instancias debemos, formular ecuaciones de cambio para el sustrato (o
sustratos), el producto (o productos), etc.
Esta fue solamente una breve introducción al área de Ingeniería de reactores biológicos, un área
más de acción para el ingeniero de procesos. Checar http://216.47.139.198/pensim/ donde se
presenta un simulador de procesos biológicos de este tipo.
Ingeniería de Reactores
69
M.Alvarez 2003