Segunda Prueba Solemne IC 320 Métodos de Optimización Ejercicio 1:

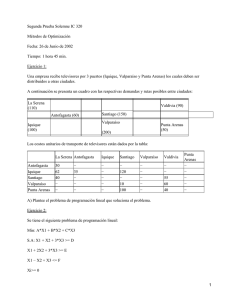
Segunda Prueba Solemne IC 320
Métodos de Optimización
Tiempo: 1 hora 45 min.
Ejercicio 1:
Una empresa recibirá cargamento marítimo de televisores por 3 puertos (Iquique, Valparaíso y Punta Arenas)
los cuales deben ser distribuidos a otras ciudades. El cargamento lo distribuye un solo barco.
Los puertos tienes los siguientes costos de internación promedio por unidad: Iquique de 20 mil, Valparaíso de
30 mil y Punta Arenas 15 mil pesos.
Por distintos motivos, existe una perdida en los puertos de entrada, de 10% en Valparaíso y 20% en Punta
Arenas, los que deben ser compensados.
Adicionalmente, el Estado, permite la internación de solo 200 unidades a través de Iquique.
A continuación se presenta un cuadro con las respectivas demandas y rutas posibles entre ciudades:
Los costos unitarios de transporte de televisores están dados por la tabla:
Antofagasta
Iquique
Santiago
Valparaíso
Punta Arenas
La Serena Antofagasta
Iquique
Santiago
Valparaíso
Valdivia
30
62
40
−
−
−
−
−
−
−
−
120
−
10
100
−
−
−
−
−
−
−
55
60
40
−
35
−
−
−
Punta
Arenas
−
−
−
−
−
A) Plantee el problema de programación lineal que soluciona el problema.
Ejercicio 2:
Se tiene el siguiente problema de programación lineal:
Min: A*X1 + B*X2 + C*X3
1
S.A: X1 + X2 + 3*X3 >= D
X1 + 2X2 + 3*X3 >= E
X1 − X2 + X3 <= F
Xi>= 0
D es el recurso asociado a la primera restricción.
E es el recurso asociado a la segunda restricción.
F es el recurso asociado a la tercera restricción.
A = 3; B = 2; C = 4; D = 5; E = 4; F = 10
Se pide:
• Resolver el problema por el método Simplex
• ¿En que intervalo puede variar A, C, D y F (en forma independiente) sin modificar la solución óptima?
• ¿Cuanto estaría dispuesto a pagar por una unidad extra del recurso D y E?
Ejercicio 3:
Se le ha escogido para acomodar las canciones del último álbun de Madonna, en la versión de cassette. Una
cinta de cassette tiene dos lados ( Lado 1 y Lado 2). Las canciones en cada lado deben sumar entre 14 y 16
minutos de duración. Cada canción tiene un nivel de aceptación dependiendo del lado donde se ubique
(medido en estrellas).
La duración, la aceptación (estrellas) y el tipo de cada canción se dan en la siguiente tabla:
Canción
1
2
3
4
5
6
Tipo
Balada−Hit
Hit
Balada
Hit
Balada
Hit
Duración
4
5
3
2
4
3
Aceptación Lado 1
**
***
*
*
****
**
Aceptación Lado 2
*******
***
**
****
**
****
La asignación de canciones debe satisfacer las siguientes condiciones:
• En cada lado debe haber exactamente 2 Baladas.
• En el lado 1 debe haber por lo menos 3 Hits.
• La canción 5 o 6 deben estar en el lado 1.
• Las canciones 2 y 4 van juntas y solo en el lado 1
A) Plantee el problema de P.L. que permite maximizar la aceptación del álbun.
2
Figure 1, Primera tabla, continuelas.
3