y M(x) viene dado por Sustituyendo convenientemente: Derivando

48
MÉTODO DE LAS FUERZAS. DESCRIPCIÓN Y COMENTARIOS
y M(x) viene dado por
Sustituyendo convenientemente:
Derivando respecto de las acciones correspondientes, y sin tener en cuenta el efecto
del esfuerzo cortante:
a.2.-
Análisis siguiendo el Primer Teorema de la Viga Conjugada, que puede enunciarse
como sigue:
El ángulo girado por la sección que corresponde a un apoyo articulado extremo de
una viga dada viene medido por la reacción en dicho apoyo de la viga conjugada.
Planteando las siguientes ecuaciones de equilibrio:
E. MARTIN & J. VALCARCEL & J. ESTEVEZ
ANÁLISIS MATRICIAL DE SISTEMAS ESTRUCTURALES
49
Y despejando adecuadamente, resulta:
En el caso que aquí nos ocupa, y aplicando el Principio de Superposición:
expresiones plenamente coincidentes con las obtenidas en el punto anterior.
Atendiendo a las expresiones [11] y [13], las ecuaciones del material, para un
miembro AB unido rígidamente, pueden expresarse de la siguiente forma:
E. MARTIN & J. VALCARCEL & J. ESTEVEZ
50
MÉTODO DE LAS FUERZAS. DESCRIPCIÓN Y COMENTARIOS
2.5.2.2.
EMPARRILLADOS PLANOS DE NODOS RÍGIDOS
En este caso, cada nodo aparecerá representado, en el vector de acciones exteriores
P, por una carga perpendicular al plano de la estructura, y dos momentos de eje contenido
en dicho plano. A este sistema le corresponde, igualmente por punto, un conjunto de
desplazamientos d constituido por un corrimiento y dos rotaciones. Con todo:
a.-
ECUACIONES DEL MATERIAL
E. MARTIN & J.VALCARCEL & J. ESTEVEZ
ANÁLISIS MATRICIAL DE SISTEMAS ESTRUCTURALES
51
La deducción de los giros $A y €>B de las secciones extremas, debidos a la acción de
los momentos Héctores MA y MB, es análoga a la desarrollada para el caso de pórticos
planos.
No obstante, aquí prescindimos de los esfuerzos axiles N (y de los correspondientes
alargamientos u), y sí contemplamos un momento torsor MT que origina rotaciones $x
alrededor de la directriz de la pieza.
En estas condiciones, la ecuación [12] se estructura de la siguiente forma:
Aplicando el Segundo Teorema de Castigliano:
2.6. COMENTARIOS EN TORNO A LA ELECCIÓN DEL SISTEMA
ISOSTATICO EQUIVALENTE
En apartados precedentes hemos expuesto que el desarrollo del proceso, en su
aplicación a estructuras estáticamente indeterminadas, pasa necesariamente por la elección
de un sistema isostático equivalente; mediante la aplicación de un conjunto de fuerzas
redundantes, que vienen así a sustituir a los vínculos sobrantes.
Cada estructura hiperestática permite un cierto número de esquemas alternativos, cada
uno de ellos asociado a un sistema de ecuaciones en principio válido y con la forma ya
E. MARTIN & J. VALCARCEL & J. ESTEVEZ
52
MÉTODO DE LAS FUERZAS. DESCRIPCIÓN Y COMENTARIOS
expuesta:
Ahora bien, en la resolución del conjunto [9], necesario para evaluar las fuerzas
redundantes Pr, pueden producirse situaciones extremadamente sensibles a los errores de
redondeo. Así, el cálculo de la diferencia entre dos cantidades muy grandes y relativamente
próximas será tanto más impreciso cuanto menor sea el número de cifras significativas con
que se opere (teniendo en cuenta que el resultado es un número comparativamente reducido).
En el mencionado susbsistema, el segundo sumando [Frr Pr] representa el conjunto
de desplazamientos que se producirán en el esquema isostático seleccionado, sobre la línea
de acción de las fuerzas redundantes, y originadas por éstas.
La matriz Frr está así constituida por los coeficientes de flexibilidad correspondientes
a las liberaciones adoptadas. Los situados sobre la diagonal principal no son sino los
desplazamientos producidos por acciones unitarias, actuando separadamente en el sentido de
las fuerzas redundantes, y en sus puntos de aplicación. Los demás elementos constituyen los
desplazamientos de cada uno de ellos, pero ahora originados por cargas unidad actuando
independientemente en lugar de cada una de las redundancias restantes. La relación entre los
coeficientes de la citada diagonal y los no incluidos en ella, da un orden de magnitud del
nivel de interacción que se establece ante las acciones redundantes seleccionadas.
En general, y con objeto de paliar las incorrecciones aludidas, debe elegirse una
combinación de liberaciones tal que la matriz Frr resulte dominada por los elementos de su
diagonal principal (esto es, con interacciones mínimas).
Se propone el siguiente ejemplo con el fin de clarificar las ideas hasta aquí expuestas:
E. MARTIN & J.VALCARCEL & J. ESTEVEZ
ANÁLISIS MATRICIAL DE SISTEMAS ESTRUCTURALES
53
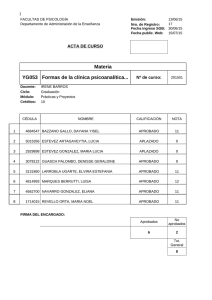
Se trata de una viga continua, con grado de indeterminación 3, y con luces las
indicadas en la figura. En estas condiciones, la igualdad [9] puede expresarse como sigue:
Multiplicando a ambos lados por la inversa de la matriz de flexibilidades Frr:
siendo
A = determinante de la matriz F,
A continuación se analizan las implicaciones que se derivan de la adopción de dos
sistemas isostáticos diferentes:
Sistema estáticamente determinado a.-).
Se liberan los apoyos intermedios, y se aplican las reacciones correspondientes como
fuerzas redundantes.
E. MARTIN & J. VALCARCEL & J. ESTEVEZ
54
MÉTODO DE LAS FUERZAS. DESCRIPCIÓN Y COMENTARIOS
Partimos de la ecuación de la elástica para una viga biapoyada sometida a la acción
de una carga concentrada y transversal a su directriz:
Con estos datos estamos en condiciones de evaluar los coeficientes de influencia
correspondientes:
(fjj es el desplazamiento del nodo i cuando actúa una fuerza R¡ unitaria)
Los restantes coeficientes pueden obtenerse por condiciones de simetría, tanto de la
estructura como de la propia matriz:
E. MARTIN & J. VALCARCEL & J. ESTEVEZ
ANÁLISIS MATRICIAL DE SISTEMAS ESTRUCTURALES
55
El determinante de la matriz, que, como hemos indicado, afecta directamente al valor
de las fuerzas redundantes {R,, R2, R3}, adopta las siguientes magnitudes en función del
redondeo con que se efectúen las operaciones:
1 cifra significativa A¿ = 51,3
2 cifras significativas Aa = 57,93
3 cifras significativas A;j = 58,593
4 cifras significativas A* = 58,6605
Se aprecian notables variaciones entre los resultados obtenidos (divergencias que aún
podrían aumentar dependiendo de la forma en que se plantee el determinante y del orden en
que se realicen los cálculos).
Sistema estáticamente determinado b.-).
Se adoptan como fuerzas redundantes los momentos Héctores que soporta la viga en
los apoyos intermedios.
En este caso, las ecuaciones que proporcionan los giros producidos en las secciones
extremas de una viga biapoyada, ante un momento aplicado en el origen, son:
Sustituyendo convenientemente:
E. MARTIN & J. VALCARCEL & J. ESTEVEZ
56
MÉTODO DE LAS FUERZAS. DESCRIPCIÓN Y COMENTARIOS
Operando, se obtiene para el determinante un valor exacto:
A t = 132
La imprecisión de cálculo obtenida en el esquema isostático a.-) frente al b.-) posee
una cierta interpretación física. En efecto, las reacciones correspondientes a los vínculos
internos son sumamente sensibles ante variaciones de su posición o frente a modificaciones
en las propiedades elásticas de los miembros.
En apartados precedentes, hemos afirmado que el Método de las Fuerzas no es
adecuado de cara a la confección de una aplicación informática, y sí para afrontar
determinados cálculos de forma manual. No obstante, y a la vista de las conclusiones aquí
expuestas, insistimos en que su uso debe producirse con una buena dosis de intuición y
capacidad de análisis, actitudes ambas que debe desarrollar todo técnico.
E. MARTIN & J. VALCARCEL & J. ESTEVEZ
ANÁLISIS MATRICIAL DE SISTEMAS ESTRUCTURALES
57
CAPITULO 3
MÉTODO DE LOS DESPLAZAMIENTOS
DESCRIPCIÓN Y COMENTARIOS
3.1. DESCRIPCIÓN DEL MÉTODO
El procedimiento pasa por satisfacer simultáneamente un cierto número de ecuaciones
que representan el equilibrio a través de la totalidad de la estructura. Su resolución
proporciona cantidades de desplazamiento que constituyen así el primer conjunto de
incógnitas del problema.
Cuando el volumen de información, conocida y desconocida, se reordena en un
formato matricial, dichas ecuaciones incorporan la matriz de rigideces; que no es sino una
síntesis de las sucesivas matrices de rigideces individuales de los distintos miembros que
componen el sistema estructural.
Atendiendo a las anteriores nociones, el Método se dice de "los Desplazamientos",
de "las Rigideces", o del "Equilibrio". El orden en que recurriremos a las consabidas
relaciones fundamentales para su aplicación es el siguiente:
a.b.c.-
LEY DE HOOKE.
COMPATIBILIDAD DE DESPLAZAMIENTOS.
ECUACIONES DE EQUILIBRIO.
Una de las diferencias fundamentales que lo distinguen del Método de las Fuerzas es
la no necesidad, por parte del analista, de asumir una selección similar a la de las fuerzas
redundantes. En apartados anteriores hemos reseñado que esta operación añadía dos
dificultades: La propia elección de liberaciones, tanto más costosa cuanto más compleja sea
la estructura; y la determinación de un esquema isostático asociado con un adecuado
comportamiento.
Por otra parte, en el procedimiento descrito debía resolverse un sistema de ecuaciones
cuyo orden era igual al número de redundancias (grado de indeterminación estática). El
sistema correlativo al Método de los Desplazamientos contendrá, en cambio, tantas
ecuaciones como grados de libertad (indeterminación cinemática), lo que supone un
incremento notable en el volumen de operaciones. Si bien esta situación puede paliarse
aplicando determinadas técnicas, no cabe duda que representa una cierta desventaja de cara
E. MARTIN & J. VALCARCEL & J. ESTEVEZ
58
MÉTODO DE LOS DESPLAZAMIENTOS. DESCRIPCIÓN Y COMENTARIOS
al cálculo manual. No obstante, y cuando nos enfrentamos a la confección de aplicaciones
informáticas, este aumento en el tiempo de cálculo resulta despreciable; especialmente si se
considera frente a las prestaciones del Método del Equilibrio en cuanto a su formalización
y sistematización.
En las siguientes secciones del presente texto procederemos a su descripción detallada,
así como al estudio de ciertas utilidades avanzadas que pueden optimizar notablemente su
implementación en ordenador.
Con objeto de abordar una descripción general del llamado Método de los
Desplazamientos, volvemos sobre el esquema de los cuatro muelles ya resuelto en capítulos
anteriores. Recordemos que el sistema se hallaba solicitado por las cargas {P4, P5}, y
desarrollaba los esfuerzos axiles internos {N,, N2, N3, N4, N5} y las fuerzas reactivas {R,,
R2, R3}En estas condiciones, procedemos a aplicar:
3.1.1. LEY DE HOOKE
Las ecuaciones constitutivas del material expresan, para cada miembro, una relación
lineal entre el esfuerzo que soporta y el alargamiento que experimenta. Esto es:
donde ki representa la rigidez del elemento vinculada al esfuerzo axil, o, de otra forma, el
esfuerzo axil desarrollado cuando el alargamiento es unitario. Como se desprende de la
expresión, la rigidez de la pieza es la inversa de la flexibilidad. Así:
En forma matricial:
E. MARTIN & J. VALCARCEL & J. ESTEVEZ
ANÁLISIS MATRICIAL DE SISTEMAS ESTRUCTURALES
[16]
N =k D
siendo
N
k
D
59
Vector de esfuerzos en la estructura.
Matriz diagonal formada por las rigideces de las piezas.
Vector que incorpora las deformaciones elásticas de los distintos miembros de
la estructura.
3.1.2. COMPATIBILIDAD DE DESPLAZAMIENTOS
Las condiciones de compatibilidad de la estructura exigen que los corrimientos de los
extremos de las piezas coincidan con los de los nodos a que se unen; todo ello a fin de
obtener un ajuste geométrico. Analizando bajo este punto de vista la configuración
deformada:
E. MARTIN & J. VALCARCEL
& J. ESTEVEZ
60
MÉTODO DE LOS DESPLAZAMIENTOS. DESCRIPCIÓN Y COMENTARIOS
siendo:
C
d
Matriz de Transformación de Desplazamientos.
Vector compuesto por los corrimientos de las articulaciones de la estructura.
3.1.3. ECUACIONES DE EQUILIBRIO
Las condiciones de equilibrio imponen que, en cada nodo de la estructura, las cargas
exteriores en él aplicadas igualan a la suma de los esfuerzos que la unión ejerce sobre los
extremos de las piezas que a ella concurren. De su aplicación se deducen las siguientes
igualdades:
P4 = Nl sena + N2 + N3 sena - N4
E. MARTIN & J. VALCARCEL & J. ESTEVEZ
ANÁLISIS MATRICIAL DE SISTEMAS ESTRUCTURALES
P = C1N
siendo:
P
61
[18]
Vector compuesto por las acciones extemas aplicadas en los nodos.
Analizando las expresiones [17] y [18] se observa que la matriz de coeficientes Cl
coincide con la transpuesta de la Matriz de Transformación de Desplazamientos C. Este
hecho se puede demostrar aplicando el Principio de Conservación de la Energía; esto es,
igualando el trabajo efectuado por las acciones exteriores y el desarrollado por los esfuerzos
internos en los distintos miembros de la estructura.
Atendiendo a la Ley de Clapeyron, el trabajo realizado por una carga P¡, cuando su
punto de aplicación i experimenta un desplazamiento 5¡ durante la deformación, adopta un
valor:
Del mismo modo, y en relación a los esfuerzos internos N¡, cuando actúan sobre un
desplazamiento en i, resulta:
Para la totalidad de la estructura se ha de cumplir:
En forma matricial:
El 8 = til D
Y sustituyendo la igualdad [17]:
Transponiendo ambos términos, se obtiene:
P = C1N
E. MARTIN & J. VALCARCEL & J. ESTEVEZ
62
MÉTODO DE LOS DESPLAZAMIENTOS. DESCRIPCIÓN Y COMENTARIOS
coincidente con la expresión [18] antes expuesta.
3.1.4. SUSTITUCIONES
Las relaciones fundamentales hasta aquí desarrolladas pueden indicarse como sigue:
N =k D
[16]
P = C1N
[18]
Reemplazando el vector N (dado por [16]) en la igualdad [18], y D (evaluado por
[17]) sobre el resultado:
Las anteriores conclusiones pueden expresarse de la siguiente forma:
[20]
K = ClkC
K constituye la Matriz de Rigidez de la estructura y representa su resistencia a la
deformación bajo la acción de las cargas exteriores. En apartados posteriores volveremos
sobre su definición e implicaciones. Retornando al ejemplo ya analizado:
E. MARTIN & J. VALCARCEL
& J. ESTEVEZ
ANÁLISIS MATRICIAL DE SISTEMAS ESTRUCTURALES
63
Desarrollando la igualdad [19]:
El anterior sistema de ecuaciones permite evaluar los desplazamientos {54, d¡}, que
constituyen el primer conjunto de incógnitas del problema.
Por otra parte, de [16] y [17]:
Sustituyendo en esta igualdad los desplazamientos 5 antes calculados, se obtienen los
esfuerzos N en los miembros de la estructura.
3.2. RESUMEN DEL PROCESO
El llamado Método de los Desplazamientos puede esquematizarse como sigue:
a.-
Establecimiento de las ecuaciones constitutivas del material, expuestas en [16]:
N=KD
b. -
Aplicación de las condiciones de compatibilidad, lo que permite construir la Matriz
de Transformación de Desplazamientos C, y el sistema [17]:
D = C¿
c.-
Planteamiento de las ecuaciones de equilibrio [18]:
E = C1N
d. -
Construcción de la Matriz de Rigidez Global K:
E. MARTIN & J. VALCARCEL & J. ESTEVEZ
64
MÉTODO DE LOS DESPLAZAMIENTOS. DESCRIPCIÓN Y COMENTARIOS
e. -
Obtención de los desplazamientos de los nodos, resolviendo para ello el sistema de
ecuaciones [19]:
/-
Cálculo de los esfuerzos en los elementos que componen la estructura, mediante la
sustitución de 6 en la igualdad [21]:
3.3. NOTACIÓN. SISTEMAS DE REFERENCIA Y CONVENIOS DE
SIGNOS
Recordaremos en primer lugar la nomenclatura básica empleada hasta el momento,
que, en lo sucesivo, vendrá referida únicamente a estructuras planas.
En cada una de las piezas rectas integrantes, se adoptará como sentido de avance
aquél que nos conduzca desde el nodo de menor numeración al opuesto. Al origen de dicho
recorrido se le denomina extremo dorsal o inicial, y al que representa su término, frontal o
final.
En la práctica, tanto los nodos como las barras se designan por cifras, si bien, y como
es lógico, con numeraciones independientes. De ahí que, para evitar confusiones, se aconseje
distinguirlas de alguna forma (recuadrando unas, o estableciendo diferencias de color o tipo
de letra). Se recuerda igualmente que el orden de numeración de las barras es indiferente.
Por el contrario, y como demostraremos en próximos apartados, conviene numerar los nodos
de forma que se reduzca, en la medida de lo posible, la máxima diferencia existente entre
los extremos de las barras.
Conforme a lo anteriormente expuesto, se elegirá para cada pieza un sistema local de
referencia, esto es, un triedro directo referido a la misma; en virtud del cual se expresarán
las magnitudes propias del elemento. Estará constituido por:
a. -
Un eje X que contenga a la directriz de la barra, y con sentido positivo idéntico al
de avance ya definido.
b.-
Un eje Y perpendicular al anterior, y situado en el plano de la estructura,
c. -
Un eje Z normal al plano mencionado.
E. MARTIN & J. VALCARCEL & J. ESTEVEZ
ANÁLISIS MATRICIAL DE SISTEMAS ESTRUCTURALES
65
Teniendo en cuenta las anteriores consideraciones, lo normal es que los ejes [Y,Z]
sean principales de inercia de la sección transversal.
Por otra parte, se adoptará un sistema global de referencia, respecto del cual se
plantearán aquellos problemas en los que no intervenga únicamente una de las piezas de la
estructura. Habitualmente se elige como eje X' uno contenido en el plano y, o bien
horizontal, o bien paralelo a una de las dimensiones de la estructura. Los ejes [Y', Z'] se
determinan imponiendo las mismas condiciones indicadas en la descripción del sistema local.
En lo que resta del presente epígrafe, concretaremos las consideraciones anteriores
para cada uno de los tipos estructurales que pretendemos estudiar. Del mismo modo, se
indicará en cada caso el convenio de signos que corresponda.
3.3.1. ESTRUCTURAS ARTICULADAS
E. MARTIN
& J. VALCARCEL & J. ESTEVEZ
66
MÉTODO DE LOS DESPLAZAMIENTOS. DESCRIPCIÓN Y COMENTARIOS
Toda estructura plana articulada está constituida por piezas rectas unidas entre sí por
sus extremos (articulaciones), que se suponen incapaces de transmitir momentos. Para que
el equilibrio de las barras sea factible, es preciso que no existan cortantes; con lo que
únicamente soportarán esfuerzos axiles.
En realidad, los nodos que definen las cerchas o celosías trianguladas no suelen ser
propiamente articulaciones. No obstante, no hay problema en incluir a estos sistemas en el
presente punto, siempre y cuando al considerar dichas uniones como perfectamente
articuladas, el conjunto no se convierta en un mecanismo.
3.3.2. ESTRUCTURAS DE NODOS RÍGIDOS
Consideraremos sistemas planos compuestos por piezas de directriz recta unidas
rígidamente en sus extremos. En estas condiciones, cada nodo puede experimentar una
rotación rígida por efecto de la flexión en los elementos que a él concurren.
3.3.2.1.
PÓRTICOS PLANOS DE NODOS RÍGIDOS
E. MARTIN & J. VALCARCEL & J. ESTEVEZ
ANÁLISIS MATRICIAL DE SISTEMAS ESTRUCTURALES
3.3.2.2.
EMPARRILLADOS PLANOS DE NODOS RÍGIDOS
E. MARTIN & J. VALCARCEL
& J. ESTEVEZ
67
68
MÉTODO DE LOS DESPLAZAMIENTOS. DESCRIPCIÓN Y COMENTARIOS
E. MARTIN & J. VALCARCEL & J. ESTEVEZ
ANÁLISIS MATRICIAL DE SISTEMAS ESTRUCTURALES
69
CAPITULO 4
RELACIONES FUNDAMENTALES EN EL MÉTODO
DE LOS DESPLAZAMIENTOS
4.1. ECUACIONES DEL MATERIAL
Las relaciones constitutivas del material permiten vincular, en cada elemento, los
esfuerzos característicos a que se encuentra sometido con los desplazamientos relativos de
sus secciones extremas.
4.1.1. ESTRUCTURAS ARTICULADAS
En este tipo estructural, cada barra soporta únicamente un esfuerzo axil, y
experimenta, por tanto, incrementos o disminuciones en su longitud. Admitiendo que la piez
responde a un comportamiento lineal, y encontrándose sometida a tracción pura, su
alargamiento total vendrá dado por:
En estas condiciones, se denomina rigidez al alargamiento al cociente:
E. MARTIN & J. VALCARCEL & J. ESTEVEZ
70
RELACIONES FUNDAMENTALES EN EL MÉTODO DE LOS DESPLAZAMIENTOS
Para piezas constituidas por un único material, de Módulo de Elasticidad Longitudinal
E, y de sección transversal A constante, resulta:
expresión que corresponde, como ya hemos apuntado, a la inversa de la flexibilidad del
elemento (ecuación [10]).
De esta forma, la igualdad [16] puede expresarse como sigue:
siendo
Af
k
D
Vector de esfuerzos axiles en los miembros de la estructura, cuyo número total
es n.
Matriz diagonal compuesta por las rigideces al alargamiento de las distintas
piezas.
Vector compuesto por las correspondientes variaciones elásticas de longitud.
4.1.2. ESTRUCTURAS DE NODOS RÍGIDOS
Centrándonos en el estudio de las estructuras planas, consideraremos los siguientes
tipos:
E. MARTIN & J. VALCARCEL
& J. ESTEVEZ