Volumen de la pirámide. - Wiki

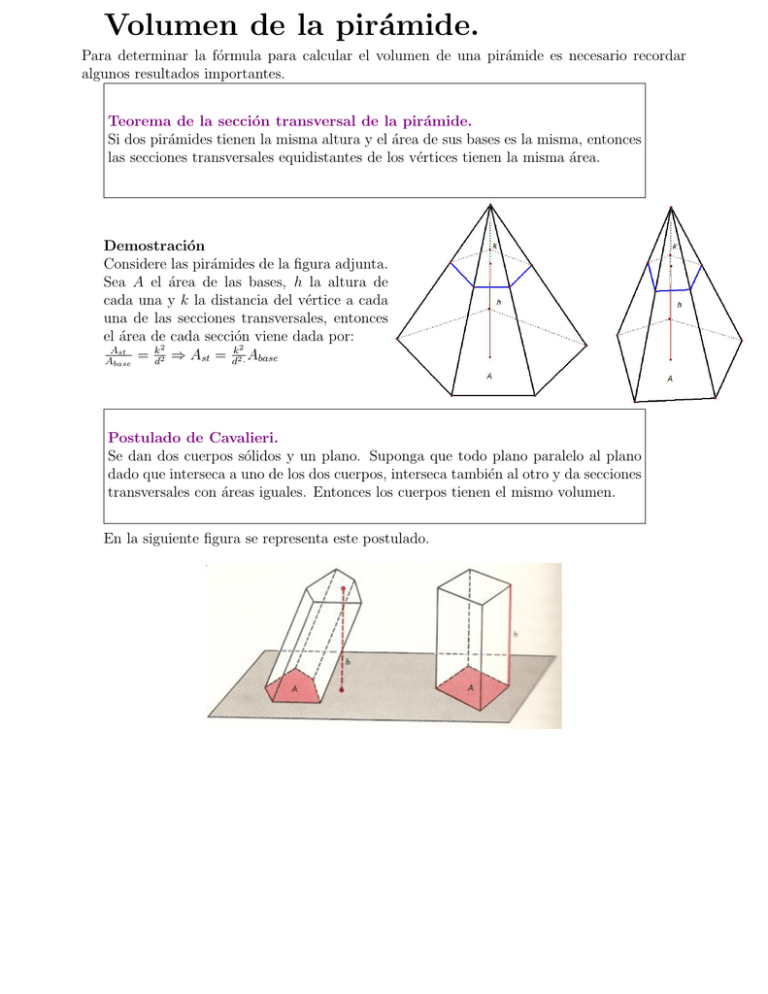
Volumen de la pirámide.
Para determinar la fórmula para calcular el volumen de una pirámide es necesario recordar
algunos resultados importantes.
Teorema de la sección transversal de la pirámide.
Si dos pirámides tienen la misma altura y el área de sus bases es la misma, entonces
las secciones transversales equidistantes de los vértices tienen la misma área.
Demostración
Considere las pirámides de la figura adjunta.
Sea A el área de las bases, h la altura de
cada una y k la distancia del vértice a cada
una de las secciones transversales, entonces
el área de cada sección viene dada por:
2
2
Ast
= kd2 ⇒ Ast = dk2 · Abase
Abase
Postulado de Cavalieri.
Se dan dos cuerpos sólidos y un plano. Suponga que todo plano paralelo al plano
dado que interseca a uno de los dos cuerpos, interseca también al otro y da secciones
transversales con áreas iguales. Entonces los cuerpos tienen el mismo volumen.
En la siguiente figura se representa este postulado.
Teorema.
El volumen de una pirámide triángular es un tercio del
producto de su altura y el área de la base.
Demostración
Considere la pirámide triángular S.ABC de
altura h. Trace AD k SB, CE k SB
con AD ∼
= SB ∼
= CE, luego el sólido
ABCSDE es un prisma triangular que tiene
la misma base y la misma altura de la
pirámide S.ABC.
El volumen del prisma es igual a:
Vprisma = (ABC) · h, pero observe que
el prisma está formado por dos pirámides,
S.ABC y S.ACED, cuya base es un paralelogramo, por lo tanto se cumple que 4ACD ∼
=
∼
4ECD, luego VS.ACD = VS.ECD
Ası́ entonces Vprisma = VS.ABC + VS.ACD +
VS.ECD .
4ABC ∼
= 4DES, entonces VS.ABC =
VS.DEC
Vprisma = 3VS.ABC
VS.ABC = 31 Vprisma
VS.ABC = 31 (ABC) · h
Teorema.
El volumen de una pirámide es un tercio del producto
de su altura y el área de la base
Demostración
Considere una pirámide de altura h y área de
la base A. Tómese una pirámide triángular
de la misma altura y la misma área de
la base, con las bases en el mismo plano.
Por el teorema de la sección transversal de
la pirámide, las secciones transversales a la
misma distancia del vértice tienen la misma
área, luego en virtud del Postulado de Cavalieri, las dos pirámides tienen el mismo volumen y ası́ el volumen de cada una de ellas
viene dado por V = 31 A · h