Leyes de Kirchhoff

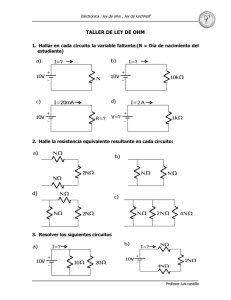
1
Leyes de Kirchhoff
Objetivo


Verificar el cumplimiento de las leyes de Kirchhoff.
Calcular la potencia disipada en el circuito.
Material







2 Amperímetro
Osciloscopio Fluke
Generador de onda
Computador
Fuente Protek
Cables de conexión
Tablero varias resistencias.
Introducción
Señales variables en el tiempo
En la corriente directa (CC) se tratan cantidades independientes del tiempo; sin
embargo, la gran mayoría de las señales eléctricas si dependen del tiempo. La
forma de alternación más simple son las ondas seno y coseno.
Esta
representación puede ser para el voltaje o la corriente.
El voltaje instantáneo
mediante la ecuación:
, se relaciona con el voltaje máximo o de pico, V p,
Escrita por Lucelly Reyes, Yonatan Zuleta y Alejandro Martinez
2
Características de la señal periódica
Período (T): Tiempo que abarca una onda completa de la señal alterna:
T ( s) 
2
 rad  2

 s  T


Frecuencia (f): Número de ciclos que se producen en un segundo:
ciclos  1
1

f  Hz 
 
s  T 2 

Valor instantáneo “v” o “i”: Es el que tiene la tensión o la corriente alterna para
cada valor de t. (Se representa con letra minúscula).
v(t )  V p sen(wt   )
i(t )  I p .sen(wt   )
o
Valores máximos (Vp) (Ip): Se corresponden con la cresta (máximo) y con el valle
(mínimo), situados en t=T/4 y en t=3T/4.
Valor medio o promedio (Componente continua de Vdc o Idc):
El valor medio de una onda periódica es por definición,
T
Vdc  Vcc 
1
v(t )dt
T 0
Para una señal senusoidal centrada en el eje de coordenadas, tenemos:
Vdc
T
T
Vp
1
1
cos 2  cos 0  0
 Vcc   v(t )dt   V p sent.dt  
T0
T0
2
Escrita por Lucelly Reyes, Yonatan Zuleta y Alejandro Martinez
3
Valor eficaz (Vrms) (Irms): El valor característico más común de una forma de
onda variante con el tiempo es su valor eficaz. En efecto, el valor eficaz se utiliza
más a menudo que el valor promedio para describir forma de onda de señales
eléctricas. La principal razón es que el valor promedio de formas de onda
periódicas simétricas es cero. Un valor de cero ciertamente no suministra mucha
información útil acerca de las propiedades de una señal. En contraste, el valor
eficaz de una forma de onda no sufre esta limitación.
El valor eficaz de una forma de onda se refiere a su capacidad de entregar
potencia. Por esta razón, algunas veces se lo llama valor efectivo.
El valor eficaz de una señal alterna es el equivalente al de una señal constante,
cuando aplicadas ambas señales a una misma resistencia durante un período
igual de tiempo, desarrollan la misma cantidad de calor. Por lo tanto, la intensidad
eficaz Vef o Vrms de una onda de voltaje variable en el tiempo se halla calculando la
potencia media disipada en la resistencia e igualándola a la potencia de c.c, o sea
T
2
Vrms
1 v(t ) 2
P
 
dt
R
T0 R
1 T
v(t ) 2 dt
T 0
Para una señal senusoidal se tiene:
Vrms 
I rms 
1 T
i(t ) 2 dt
T 0
1 T
1 T 2 2
2 2 1  cos 2t 
v(t ) 2 dt 
V p sen t.dt  V p


 dt
T 0
T 0
T 0 
2

T
Vrms 
Vrms  V p
2  T sen2  sen(0)  V p

 2
T  4
2

Marco teórico de leyes de Kirchhoff
Hasta ahora se ha descrito el comportamiento de los circuitos simples, en base a
los conceptos de potencial, corriente, resistencia y se ha utilizado la ley de Ohm
esencialmente. En esta práctica se utiliza un conjunto más general de principios
Escrita por Lucelly Reyes, Yonatan Zuleta y Alejandro Martinez
4
conocidos como leyes de kirchhoff, para circuitos en redes eléctricas más
complejas.
Las leyes de Kirchhoff son una consecuencia directa de las leyes básicas del
Electromagnetismo (Leyes de Maxwell)
Para poder enunciar la primera Ley de Kirchhoff hay que definir:



Rama: uno o más elementos de circuitos conectados en serie en camino
abierto.
Nodo: como el punto de unión de dos o más ramas de un circuito.
Malla: La unión de dos o más ramas en camino cerrado.
Nodo
Malla
La primera ley de Kirchhoff
Se basa en la ley de conservación de la carga eléctrica, y establece que:
"la suma de la corrientes en todo nodo
debe ser siempre igual a cero":
Esto es la cantidad de carga que entra a un
nodo cualquiera en un cierto instante, es
igual a la cantidad de carga que sale de
ese nodo.
Ejemplo: tenemos un nodo donde se unen un terminal de una resistencia,
bombillo, fuente de voltaje y un alambre. En forma muy arbitraria podemos tomar
que las corrientes que entran van a ser positivas y las que salen por tanto seran
negativas.
Escrita por Lucelly Reyes, Yonatan Zuleta y Alejandro Martinez
5
La segunda ley de Kirchhoff
La segunda regla se deduce de la conservación de la energía. Es decir, cualquier
carga que se mueve en torno a cualquier circuito cerrado (sale de un punto y llega
al mismo punto) debe ganar tanta energía como la que pierde.
Se basa en la conservación de la energía, y establece que: " la suma de las
diferencias de potencial en cualquier entorno conductor cerrado de la red eléctrica,
debe ser siempre igual a cero".
Recuérdese que la diferencia de
potencias entre dos puntos a y b es el
trabajo (energía) por unidad de carga
que adquiere o se pierde al mover la
carga
desde
a
hasta
b.
matemáticamente:
Para aplicar correctamente la segunda ley de Kirchhoff, se recomienda asumir
primero un sentido de recorrer la malla. Una vez hecho esto se asigna signos
positivos a todas las tensiones de aquellas ramas donde se entre por el terminal
positivo en el recorrido de la malla y se asigna signos negativos cuando entre por
el terminal negativo de la rama.
Un circuito simple puede analizarse utilizando la ley de Ohm y las reglas de
combinaciones en serie y paralelo de resistencias. Muchas veces no es posible
reducirlo a un circuito de un simple lazo. El procedimiento para analizar un circuito
más complejo se simplifica enormemente al utilizar las Leyes de Kirchhoff.
Normalmente, en tales problemas algunos de las fem, corriente y resistencias son
conocidas y otras desconocidas. El número de ecuaciones obtenidas de las reglas
de Kirchhoff ha de ser siempre igual al número de incógnitas, para poder
solucionar simultáneamente las ecuaciones.
Ejemplo de circuito en serie
Escrita por Lucelly Reyes, Yonatan Zuleta y Alejandro Martinez
6
R1
R2
1.5kΩ
240Ω
R3
2kΩ
Vi
12 V
En este circuito solo hay un camino para los electrones por tanto solo hay una
malla y la corriente es la misma para todas las resistencias.
R1
R2
1.5kΩ
240Ω
Vi
12 V
R3
2kΩ
i
Ley de malla
Ley de Ohm
Combinando las ecuaciones 1 y 2 tenemos
Esto lo que significa es que podemos remplazar nuestro circuito por uno
equivalente, por el que pasa la misma corriente i.
Req
3.74kΩ
Vi1
12 V
i
Comprobación de las leyes de Kirchhoff
Escrita por Lucelly Reyes, Yonatan Zuleta y Alejandro Martinez
7
Se mide el voltaje de la fuente de alimentación, observe que se ha conectado una
fuente de DC, lo que significa que el voltaje de la fuente se mantiene constante en
el tiempo mientras el experimentador no cambie su valor.
i=3.209mA
Desconectando el voltímetro de la fuente y conectándolo a la resistencia R1 se
mide la caída de potencial de esta.
El valor medido debe coincidir con la Ley de Ohm la cual nos dice que la
diferencia de potencial en esa resistencia es
Escrita por Lucelly Reyes, Yonatan Zuleta y Alejandro Martinez
8
Se hace lo mismo para las otras resistencias
Si remplazamos estos valores en la ecuación 1 se tiene
ecuación de conservación de energía
Escrita por Lucelly Reyes, Yonatan Zuleta y Alejandro Martinez
9
Potencia
La potencia eléctrica es la relación de paso de energía por unidad de tiempo; es
decir, la cantidad de energía entregada o absorbida por un elemento en un tiempo
determinado (
). La unidad en el Sistema Internacional de Unidades es
el vatio o watt, que es lo mismo.
Cuando se trata de corriente continua (CC) la potencia eléctrica desarrollada en un
cierto instante por un dispositivo de dos terminales, es el producto de la diferencia
de potencial entre dichos terminales y la intensidad de corriente que pasa a través
del dispositivo. Por esta razón la potencia es proporcional a la corriente y a la
tensión. Esto es,
Para el ejemplo anterior la potencia entregada por la fuente es
Mientras que la potencia disipada por cada resistencia del circuito es
Ejemplo de circuito en paralelo
+
Lo primero que se debe hacer es identificar los nodos donde existen más de dos
ramas(o caminos) por los que los electrones pueden ir.
Escrita por Lucelly Reyes, Yonatan Zuleta y Alejandro Martinez
10
Como se puede observar en la figura los electrones salen del borne positivo de la
fuente y llegan a un punto común donde hay 2 ramas o caminos, a este punto lo
identificaremos como el primer nodo (a), en forma simular tendremos otro nodo (b)
donde las electrones se encuentras de nuevo para ir todos por el mismo camino
de retorno al borne negativo de la fuente, de esta manera han recorrido toda la
malla principal.
Ley de nodos
Ley de Ohm
donde
por tanto
Escrita por Lucelly Reyes, Yonatan Zuleta y Alejandro Martinez
11
Escrita por Lucelly Reyes, Yonatan Zuleta y Alejandro Martinez
12
Como se puede observar se cumple la Ley de nodos de Kirchhoff
Procedimiento


Seleccione 3 resistencias para su experimento. Mida con el multímetro la
resistencia de cada una de ellas.
Haga una lectura del valor de las resistencias interpretando el código de
colores dado por el fabricante, tome como ayuda la interfaz del laboratorio y
compare con el valor medido con el multímetro.
R1±∆R1
R2±∆R2
R3±∆R3
Multimetro
Codigo
Montaje_1
Escrita por Lucelly Reyes, Yonatan Zuleta y Alejandro Martinez
R4±∆R4
R5±∆R5
13
 Procedimiento para la fuente DC


Arme el circuito de la figura anterior en el simulador multisim
Corra la simulación y halle la caída de potencial en cada uno de los
elementos resistivos como también la corriente que pasa por ellos.
 Monte el circuito y conéctelo a la fuente como se indica en la figura.
 Ajuste el Voltaje de salida de la Fuente al valor indicado por el profesor
 Mida el voltaje V y la corriente en cada resistencia.
 Identifique los nodos y mallas presentes en el circuito y verifique las
leyes de Kirchhoff.
 Calcule la potencia disipada por cada resistencia.
 Halle las resistencias equivalentes del circuito. ¿Cuál es la potencia
disipada por la fuente de alimentación?
 Mida la resistencia equivalente con el multimetro. ¿Concuerda con lo
esperado?
 ¿Cuál es el significado físico de que su cumpla la regla de las mallas?
¿La regla de los nodos?
 Repita lo anterior para los circuitos en paralelo y para el circuito serie
paralelo
 Procedimiento para la fuente AC
Escrita por Lucelly Reyes, Yonatan Zuleta y Alejandro Martinez
14












Arme el circuito anterior en el simulador multisim
Corra la simulación y halle la caída de potencial en cada uno de los
elementos resistivos como también la corriente que pasa por ellos.
Monte el circuito y conéctelo a la fuente como se indica en la figura.
Ajuste el Voltaje de salida de la Fuente una de señal alterna (seno) y
seleccione una frecuencia de 1000 KHz.
Mida con el osciloscopio el voltaje de pico, corriente de pico y la
frecuencia en cada resistencia.
Calcule el voltaje RMS para cada resistencia como:
Identifique los nodos y mallas presentes en el circuito y verifique las
leyes de Kirchhoff.
Calcule la potencia disipada por cada resistencia.
Halle las resistencias equivalentes del circuito. ¿Cuál es la potencia
disipada por la fuente de alimentación?
Mida la resistencia equivalente con el multimetro. ¿Concuerda con lo
esperado?
¿Cuál es el significado físico de que su cumpla la regla de las mallas?
¿La regla de los nodos?
Repita lo anterior para los circuitos en paralelo y para el circuito serie
paralelo
Escrita por Lucelly Reyes, Yonatan Zuleta y Alejandro Martinez