Apunte - Ejercicio Física Resuelto

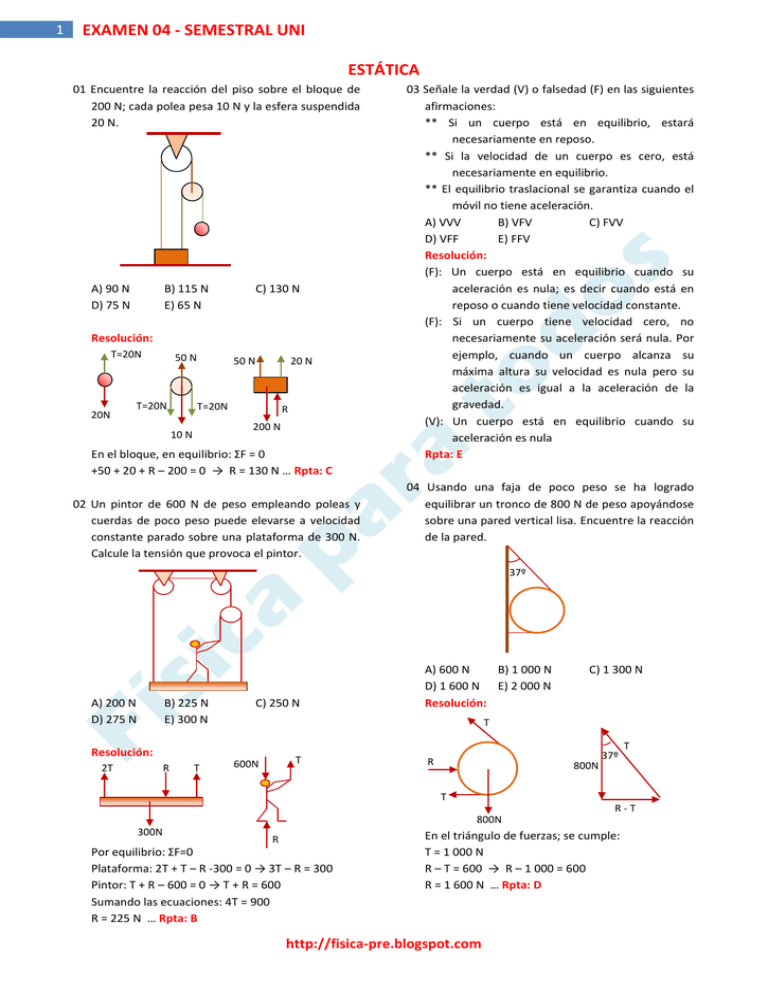
1
EXAMEN 04 - SEMESTRAL UNI
ESTÁTICA
01 Encuentre la reacción del piso sobre el bloque de
200 N; cada polea pesa 10 N y la esfera suspendida
20 N.
A) 90 N
D) 75 N
B) 115 N
E) 65 N
C) 130 N
Resolución:
T=20N
20N
50 N
T=20N
50 N
20 N
T=20N
R
200 N
10 N
En el bloque, en equilibrio: ΣF = 0
+50 + 20 + R – 200 = 0 → R = 130 N … Rpta: C
02 Un pintor de 600 N de peso empleando poleas y
cuerdas de poco peso puede elevarse a velocidad
constante parado sobre una plataforma de 300 N.
Calcule la tensión que provoca el pintor.
03 Señale la verdad (V) o falsedad (F) en las siguientes
afirmaciones:
** Si un cuerpo está en equilibrio, estará
necesariamente en reposo.
** Si la velocidad de un cuerpo es cero, está
necesariamente en equilibrio.
** El equilibrio traslacional se garantiza cuando el
móvil no tiene aceleración.
A) VVV
B) VFV
C) FVV
D) VFF
E) FFV
Resolución:
(F): Un cuerpo está en equilibrio cuando su
aceleración es nula; es decir cuando está en
reposo o cuando tiene velocidad constante.
(F): Si un cuerpo tiene velocidad cero, no
necesariamente su aceleración será nula. Por
ejemplo, cuando un cuerpo alcanza su
máxima altura su velocidad es nula pero su
aceleración es igual a la aceleración de la
gravedad.
(V): Un cuerpo está en equilibrio cuando su
aceleración es nula
Rpta: E
04 Usando una faja de poco peso se ha logrado
equilibrar un tronco de 800 N de peso apoyándose
sobre una pared vertical lisa. Encuentre la reacción
de la pared.
37º
A) 200 N
D) 275 N
B) 225 N
E) 300 N
C) 250 N
R
T
C) 1 300 N
T
Resolución:
2T
A) 600 N
B) 1 000 N
D) 1 600 N E) 2 000 N
Resolución:
T
600N
R
800N
37º
T
T
R-T
800N
300N
R
Por equilibrio: ΣF=0
Plataforma: 2T + T – R -300 = 0 → 3T – R = 300
Pintor: T + R – 600 = 0 → T + R = 600
Sumando las ecuaciones: 4T = 900
R = 225 N … Rpta: B
En el triángulo de fuerzas; se cumple:
T = 1 000 N
R – T = 600 → R – 1 000 = 600
R = 1 600 N … Rpta: D
http://fisica-pre.blogspot.com
2
EXAMEN 04 - SEMESTRAL UNI
05 En la viga de peso despreciable que se muestra en
la figura, determine las reacciones en los puntos A
y C. BC = 0,7 m; AB = 0,5 m. La fuerza F= 400 N
actúa en el punto medio de AB y la pared vertical
es lisa.
R cosβ R cosβ
R
R
β
β
T
β β
T cosα
α
A
B
T senα
37º
R cosβ
F
º
R
P
C
A) 80 N; 600
º N
C) 60 N; 300 N
E) 80 N; 300 N
Resolución:
B) 80 N; 408 N
D) 50 N; 400 N
0,25 m
0,25 m
37º
A
RA
º
º
En el cilindro superior: 2 Rcosβ = 2P
Luego: Rcosβ = P … (I)
En el cilindro de la derecha: Rsenβ = Tsenα ..(II)
Tcosα = Rcosβ + P … (III)
Resolviendo las ecuaciones: Tgβ = 2Tgα … Rpta B
07 Una varilla de 40 cm de longitud es doblada en su
punto medio B formando 37º. Calcular el valor de
“x” (en cm) para que el lado BC permanezca en
posición vertical. La varilla es de material uniforme
y homogéneo.
F=400N
º
0,7 m
º
B
C
RC
β
Por equilibrio: ΣF=0
º
B
R senβ
2P
º
º
37º
x
º
Segunda
condición de equilibrio: ΣM = 0
+RA · (0,7 + 0,3) – 400 · (0,25 cos37º) = 0
RA – 400 (0,2) = 0 → RA = 80 N
Primera condición de equilibrio: ΣF = 0
RC
A
C
A) 5
B) 10
D) 20
E) Faltan datos
Resolución:
F=400N
C) 15
T
b B
RA=80N
x
→
… Rpta:B
06 Dos cilindros iguales están suspendidos de hilos
inextensibles de idéntica longitud. Entre ellos se
pone otro cilindro de doble masa. Halle Tgβ, si los
hilos forman un ángulo 2α.
2α
β
A) Tgα
D) 4Tgα
B) 2Tgα
E) 5Tgα
C) 3Tgα
O
P
a
20cm
10cm
A
P
P
En una barra uniforme y homogénea, se cumple
que su peso es directamente proporcional a su
longitud.
Aplicando 2da condición de equilibrio: ΣMo=0, con
respecto al punto de suspensión “O”:
+P(a) – P(b) =0 → a = b → PO = OB
Como P es punto medio de AB: PO + OB = 10 cm
Luego: PO = 5 cm → x = AP + PO
x = 10 + 5 → x = 15 cm … Rpta: C
http://fisica-pre.blogspot.com
3
EXAMEN 04 - SEMESTRAL UNI
08 Un alambre metálico de peso homogéneo y
uniforme se ha doblado y puesto en equilibrio tal
como se representa en el diagrama. La longitud de
éste alambre es 4a. Calcular el ángulo “θ” que se
establece en el equilibrio.
Aplicando la 2da condición de equilibrio, con
respecto al punto de suspensión: ΣM = 0
L + 8L -2x – x + 2L = 0 → x = 3,7 L … Rpta: C
a
10 Se muestran dos poleas soldadas concéntricas de
radios r y 2r cuya masa total es “m” al igual que el
bloque. Calcúlese la fuerza con que la polea mayor
presiona el piso.
θ
a
4a
A) 30º
B) 37º
D) 53º
E) 60º
Resolución:
C) 45º
T
m
m
a
a
P
n
θ
θ
A) 0,5mg
B) 1,0mg
D) 2,0 mg
E) 2,5 mg
Resolución:
2a
+
+
-
2P
→
09 Una barra metálica de longitud L y peso 2W es
encolada con otra barra cilíndrica de madera de
longitud 4L y peso W. ¿A qué distancia del extremo
libre de madera debe suspenderse la barra
compuesta tal que permanezca equilibrada
horizontalmente?
A) 3,3L
B) 3,5L
C) 3,7L
D) 3,9L
E) Faltan datos.
Resolución:
mg
R
2L
2L
2W
-
Aplicando la 2da condición de equilibrio con
respecto al centro de las poleas: ΣM = 0
El peso de las poleas y la reacción en el piso, no
producen momento.
+F (2r) – mg (r) = 0 → F = 0,5 mg
En la ecuación (I): 0,5mg + R = 2mg
R = 1,5 mg … Rpta: C
x
L/2
r
Aplicando la 1ra condición de equilibrio: ΣF = 0
+F + R – mg – mg = 0 → F + R = 2mg … (I)
θ = 53º … Rpta: D
T
F
r
Aplicando la 2da condición de equilibrio, con
respecto al punto de suspensión: ΣM = 0
+P(2m) + P(m) – 2P(n) = 0 → 3m = 2n
W
+
+
mg
P
L/2
C) 1,5mg
http://fisica-pre.blogspot.com